Thoth Children!!|
Pop技術
-
K点が三角形の内側か判定したい
-
-
Sロボットの力制御の種類
-
K同次変換行列
-
-
SGAN
-
Kインピーダンス制御
-
-
S重力補償機構
-
Kベクトルを特定の平面に射影したい
-
-
S点群から検出したい
-
Kベクトルを別のベクトルに射影したい
-
-
S気体の可視化手法
-
Kアドミッタンス制御
-
-
Sロボットエンドエフェクタの位置制御
-
K行列を分解して上下三角行列が欲しい
-
-
Sニューラルネットワーク
-
K点が直線上の右か左にあるか判定したい
-
-
S逆運動学
-
Kヤコビ行列による逆運動学
-
-
Sオプティカルフロー
-
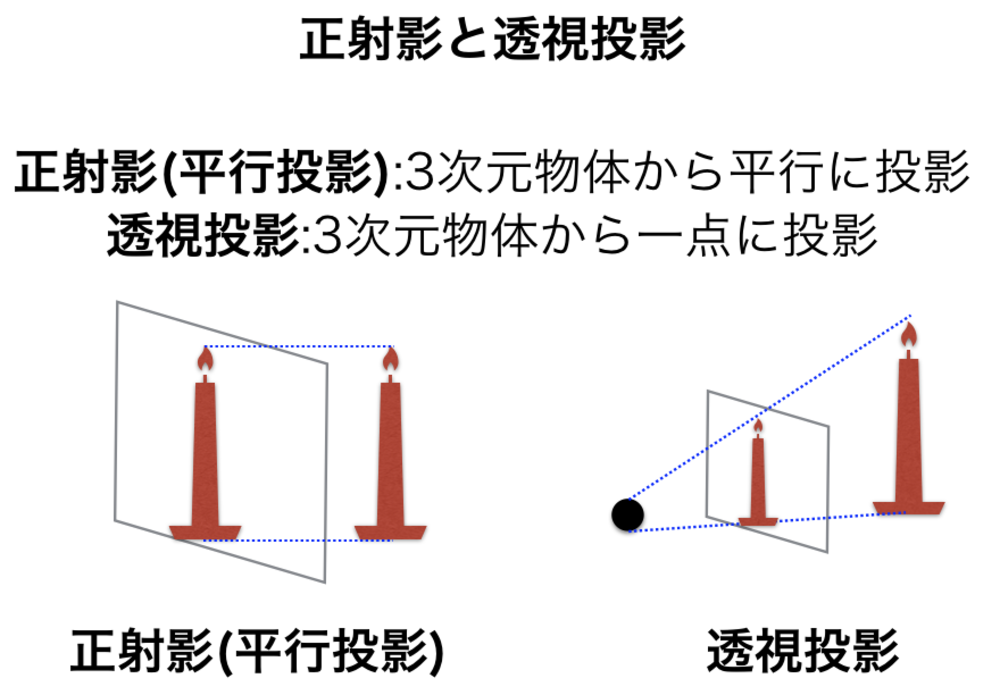
Kピンホールとレンズの違いを知りたい
-
-
S点群を間引きたい
-
K時系列間の類似度計算を選ぶ
-
-
Sニューラルネット学習の工夫
-
Kパーティクルフィルタ
-
-
S点群をデータ構造で持つ
-
Kシャドウグラフによる可視化
-
-
SRELU系活性化関数
-
K多変数関数の極大極小を判定したい
-
-
S点群から特徴量を出したい
-
Kシンプルに逆行列を求めたい
-
-
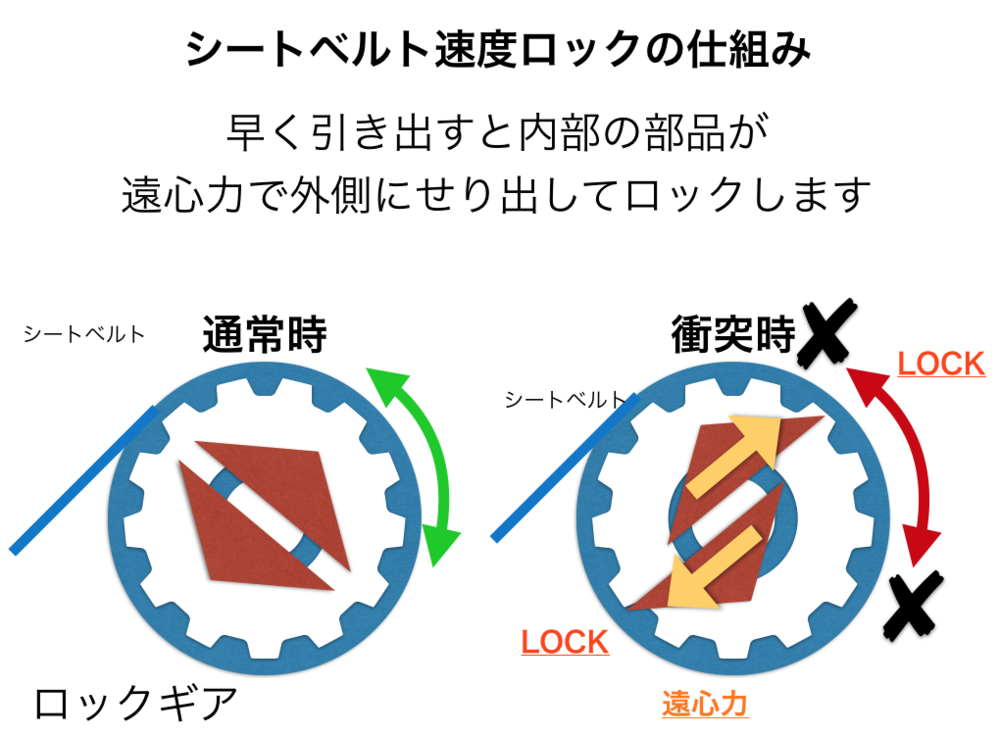
Sシートベルトの仕組みを知りたい
-
Kグラッドストーン・デールの式
-
-
Sベクトル間の類似度が欲しい
-
K力制御
-
-
SConvolution
-
K平面と平面のなす角度
-
-
S時系列間の類似度が欲しい
-
K確率分布間の差異で類似度を求めたい
-
-
Sいろいろな距離が欲しい
-
KCTC損失関数
-
-
S極大極小鞍点か判定したい
-
K勾配に注目したオプティカルフロー
-
-
S二値化フィルタ
-
Kシュリーレン法
-
-
S活性化関数基本
-
K点群データから法線算出をしたい
-
-
SSigmoid系活性化関数
-
KLucas Kanade法
-
-
S和裁くけ方種類
-
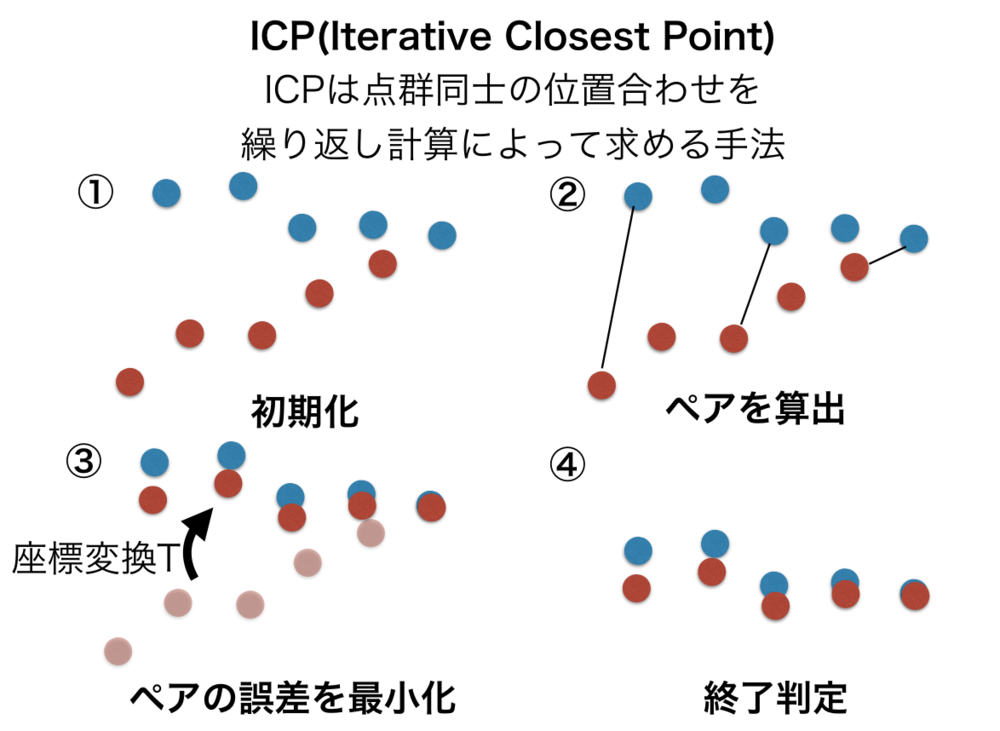
K点群から最近傍点を検出したい
-
-
SPooling
-
K点群を平面に近似したい
-
-
SDeepLearningとは
-
Kオプティカルフローとは
-
-
S点の幾何的な性質の判定をしたい
-
Kグレンジャー因果検定
-
-
SAdam系最適化関数
-
K点群の形状的局所特徴量を出したい
-
-
S点群から法線を出したい
-
K点が線上にあるか判定したい
-
-
S点群処理を実装したい
人気分野/目的
SNS