ギブスの不等式

ギブスの不等式は、二つの確率分布の間に成立する不等式.この不等式をどちらかにまとめたものはカルバック・ライブラー情報量に等しく、カルバック・ライブラー情報量が常に0以上であることを示す式を得られる.

この章を学ぶ前に必要な知識

条件

効果

ポイント

ギブスの不等式は、二つの離散的な確率分布の間に成立する不等式.この不等式をどちらかにまとめたものはカルバック・ライブラー情報量に等しく、カルバック・ライブラー情報量が常に0以上であることを示す式を得られる.	ギブスの不等式とは
ギブスの不等式は二つの確率分布$p_i,q_i$を用いて以下の式で表される.ここでは離散のみ紹介. $$-\Sigma_{i=1}^n p_i log_2(p_i) \leqq -\Sigma_{i=1}^n p_i log_2(q_i) $$ これをまとめると $$0 \leqq \Sigma_{i=1}^n p_i log_2(p_i) -\Sigma_{i=1}^n p_i log_2(q_i) \\ 0 \leqq \Sigma_{i=1}^n p_i (log_2(p_i) - log_2(q_i))\\ 0 \leqq \Sigma_{i=1}^n p_i (log_2(\frac{p_i}{q_i} )) = KL Divergence $$ このようにカルバック・ライブラー情報量が0以上であることを示している. 導出導出は、イェンセンの不等式を用いて行います. $$-\Sigma_{i=1}^n p_i (log_2(\frac{p_i}{q_i} )) = \Sigma_{i=1}^n p_i (log_2(\frac{q_i}{p_i } )) \leqq log(\Sigma_{i=1}^n p_i \frac{p_i}{q_i}) \\ = log(\Sigma_{i=1}^n p_i \frac{q_i}{p_i}) \\ = log(\Sigma_{i=1}^n q_i ) = log(1) = 0 $$ $\Sigma_{i=1}^n q_i $は確率を全て足し合わせるため1となります.	ギブスの不等式とその導出
イェンセンの不等式についてはリンクを参照願います.	イェンセンの不等式

この章を学んで新たに学べる

Comments

知識: イェンセンの不等式

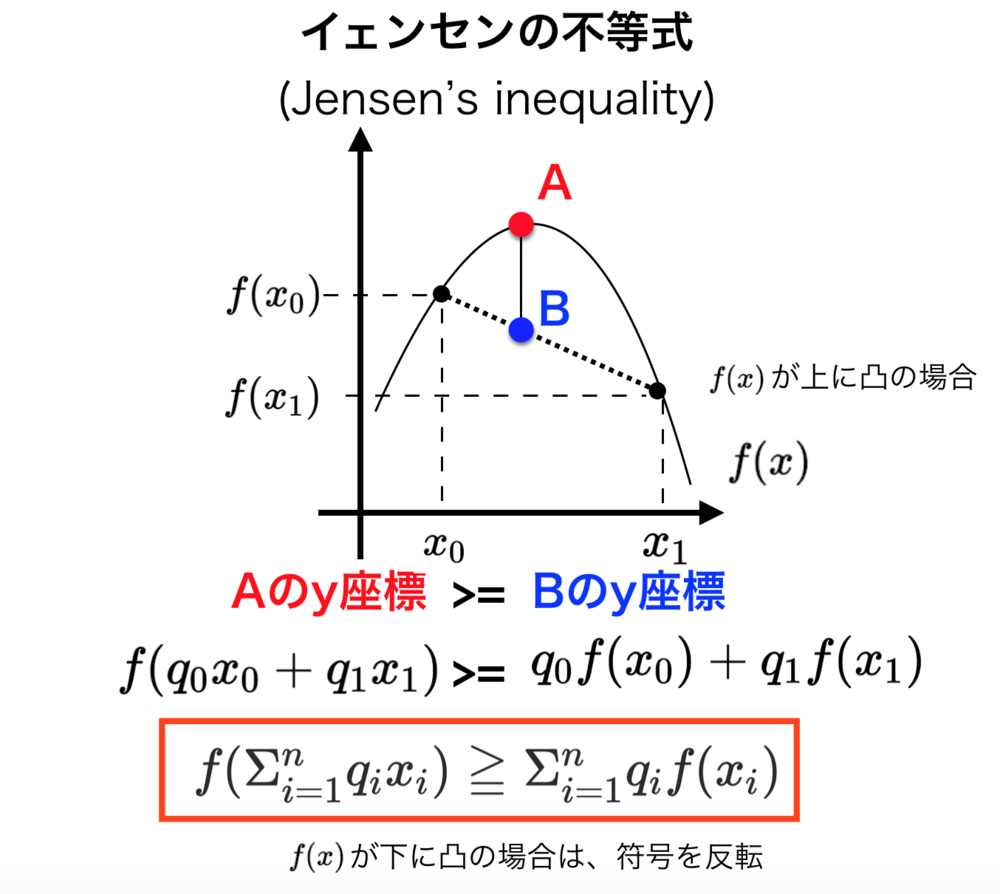
イェンセンの不等式(Jensen Inequality)とは、上に凸な関数f(x)とn個の変数x1~xnを使って表される不等式.全て足したら1となる係数q1~qnを使って、f(Σ(qi * xi)) >= Σ(qi * f(xi))が成立して、これをイェンセンの不等式と呼ぶ.

ギブスの不等式は、二つの離散的な確率分布の間に成立する不等式.この不等式をどちらかにまとめたものはカルバック・ライブラー情報量に等しく、カルバック・ライブラー情報量が常に0以上であることを示す式を得られる.	ギブスの不等式とは
ギブスの不等式は二つの確率分布\(p_i,q_i\)を用いて以下の式で表される.ここでは離散のみ紹介. $$-\Sigma_{i=1}^n p_i log_2(p_i) \leqq -\Sigma_{i=1}^n p_i log_2(q_i) $$ これをまとめると $$0 \leqq \Sigma_{i=1}^n p_i log_2(p_i) -\Sigma_{i=1}^n p_i log_2(q_i) \\ 0 \leqq \Sigma_{i=1}^n p_i (log_2(p_i) - log_2(q_i))\\ 0 \leqq \Sigma_{i=1}^n p_i (log_2(\frac{p_i}{q_i} )) = KL Divergence $$ このようにカルバック・ライブラー情報量が0以上であることを示している. 導出導出は、イェンセンの不等式を用いて行います. $$-\Sigma_{i=1}^n p_i (log_2(\frac{p_i}{q_i} )) = \Sigma_{i=1}^n p_i (log_2(\frac{q_i}{p_i } )) \leqq log(\Sigma_{i=1}^n p_i \frac{p_i}{q_i}) \\ = log(\Sigma_{i=1}^n p_i \frac{q_i}{p_i}) \\ = log(\Sigma_{i=1}^n q_i ) = log(1) = 0 $$ \(\Sigma_{i=1}^n q_i \)は確率を全て足し合わせるため1となります.	ギブスの不等式とその導出
イェンセンの不等式についてはリンクを参照願います.	イェンセンの不等式