-
 @ThothChildren
@ThothChildren
- 2019.1.28
- PV 370
Convolutionの誤差逆伝播
ー 概要 ー
畳み込み層(Convolution層)の誤差逆伝播の計算についてのみまとめているページです.Convolutionの誤差逆伝播では、後続層からの入力と180度回転したConvolution層のパラメータ、順伝播の入力値を使って計算します.
この章を学ぶ前に必要な知識
条件
- Convolution層(畳み込み層)の誤差逆伝播のみ
ポイント
- 誤差逆伝播計算に必要なのは、後続層からの誤差、Convolution層のパラメータ、順伝播時の入力
- 誤差逆伝播計算の出力は、前の層への誤差とパラメータ更新量
- 行列計算によって双方求めることができる
解 説
畳み込み層(Convolution層)の誤差逆伝播の計算についてのみまとめているページです.その計算の導出を簡単に紹介します.
Convolutionの誤差逆伝播では、
計算に必要なもの
・後続層からの入力誤差
・180度回転したConvolution層のパラメータ
・順伝播の入力値
を使って計算します.
処理によって得られるもの
・パラメータwの更新量
・前の層に送る誤差 | Convolutionの誤差逆伝播 |
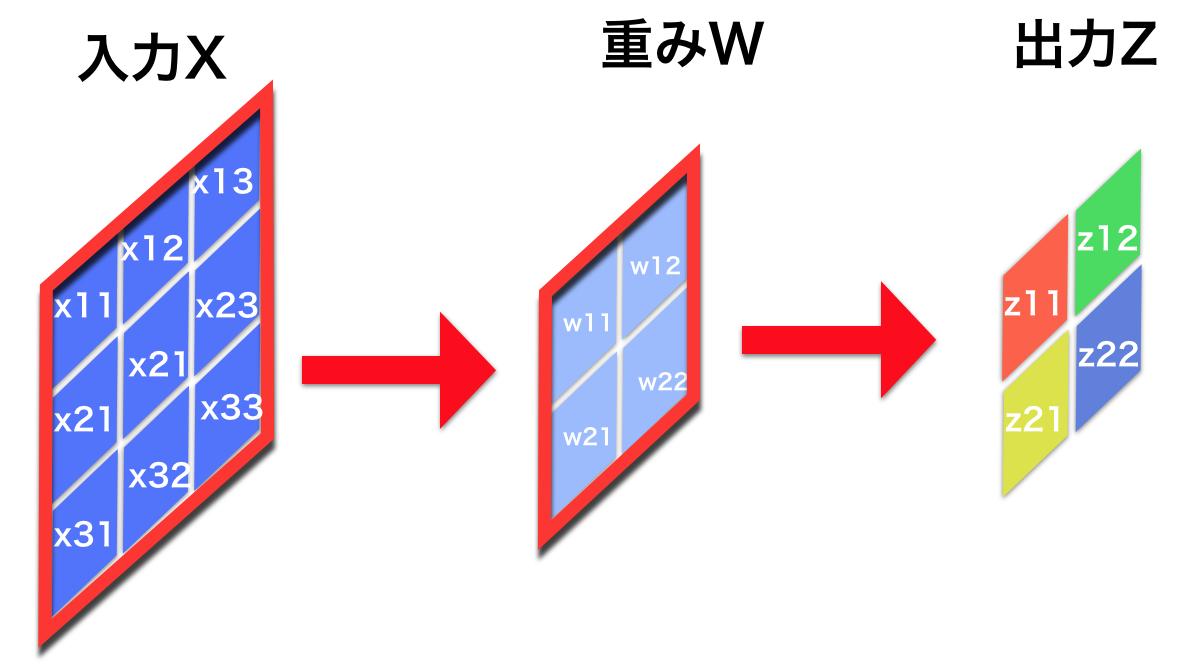 | 以下のような入力と重みと出力を考える.
(https://urusulambda.wordpress.com より引用) |
先に最終的な計算がどのようなものかを示します.
勾配法による更新であれば以下のような更新を行います.
$$w_{t+1} = w_t - \mu \frac{\partial E}{\partial w }$$
この\(\frac{\partial E}{\partial w }\)は、後続する層から伝播されてくる誤差\(\frac{\partial E}{\partial z} \)を使って以下の計算で求まります.
パラメータ更新\(\frac{\partial E}{\partial w }\) の算出
$$\frac{\partial \boldsymbol{ E}}{\partial \boldsymbol{ w} } \\
= \begin{pmatrix} \frac{\partial E}{\partial w_{11}} \\ \frac{\partial E}{\partial w_{12}} \\ \frac{\partial E}{\partial w_{21}} \\ \frac{\partial E}{\partial w_{22}} \end{pmatrix} \\
= \begin{pmatrix}
\frac{\partial E}{\partial z_{11}} x_{11} + \frac{\partial E}{\partial z_{12}}x_{12} + \frac{\partial E}{\partial z_{21}}x_{21} + \frac{\partial E}{\partial z_{22}} x_{22} \\
\frac{\partial E}{\partial z_{11}} x_{12} + \frac{\partial E}{\partial z_{12}}x_{13} + \frac{\partial E}{\partial z_{21}}x_{22} + \frac{\partial E}{\partial z_{22}} x_{23} \\
\frac{\partial E}{\partial z_{11}} x_{21} + \frac{\partial E}{\partial z_{12}}x_{22} + \frac{\partial E}{\partial z_{21}}x_{31} + \frac{\partial E}{\partial z_{22}} x_{32} \\
\frac{\partial E}{\partial z_{11}} x_{22} + \frac{\partial E}{\partial z_{12}}x_{23} + \frac{\partial E}{\partial z_{21}}x_{32} + \frac{\partial E}{\partial z_{22}} x_{33 } \\
\end{pmatrix}$$
前の層に計算して渡す誤差
次の計算は、前の層に渡す誤差\(\frac{\partial E}{\partial x}\)を求める計算です.この\(\frac{\partial E}{\partial x}\)は次の層にとっては\(\frac{\partial E}{\partial z}\)になります.
$$\frac{\partial \boldsymbol{ E}}{\partial \boldsymbol{ x} } \\
= \begin{pmatrix} \frac{\partial E}{\partial x_{11}} \\ \frac{\partial E}{\partial x_{12}} \\ \frac{\partial E}{\partial x_{21}} \\ \frac{\partial E}{\partial x_{22}} \\
\vdots
\end{pmatrix} \\
= \begin{pmatrix}
\frac{\partial E}{\partial z_{11}} w_{11} + \frac{\partial E}{\partial z_{12}}\cdot 0 + \frac{\partial E}{\partial z_{21}}\cdot 0 + \frac{\partial E}{\partial z_{22}}\cdot 0 \\
\frac{\partial E}{\partial z_{11}} w_{12} + \frac{\partial E}{\partial z_{12}}w_{11} + \frac{\partial E}{\partial z_{21}}\cdot 0 + \frac{\partial E}{\partial z_{22}} \cdot 0 \\
\frac{\partial E}{\partial z_{11}} w_{21} + \frac{\partial E}{\partial z_{12}}\cdot 0 + \frac{\partial E}{\partial z_{21}}w_{11} + \frac{\partial E}{\partial z_{22}} \cdot 0 \\
\frac{\partial E}{\partial z_{11}} w_{22} + \frac{\partial E}{\partial z_{12}}w_{21} + \frac{\partial E}{\partial z_{21}}w_{12} + \frac{\partial E}{\partial z_{22}} w_{11} \\
\vdots
\end{pmatrix}$$
| 誤差逆伝播の計算 |
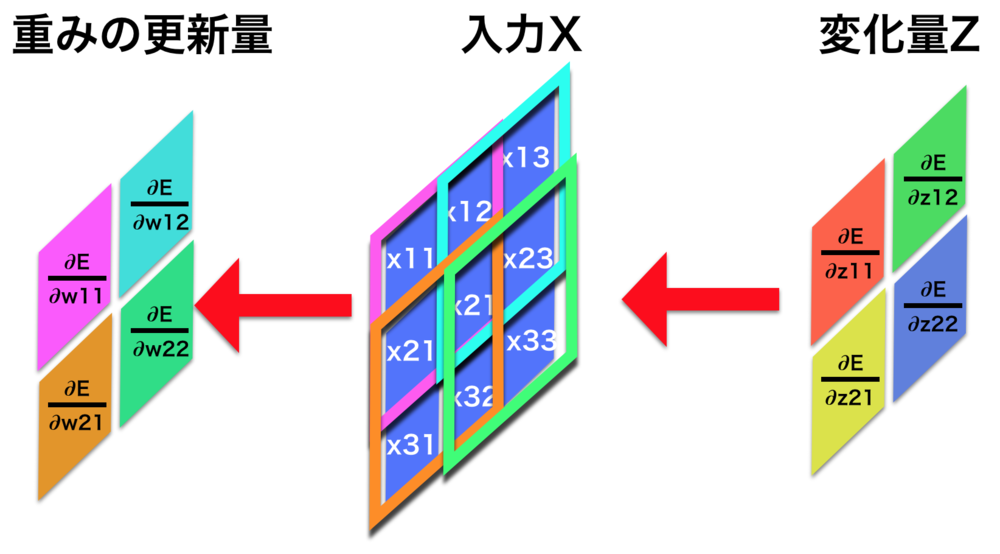 | パラメータの更新量の計算過程を可視化 |
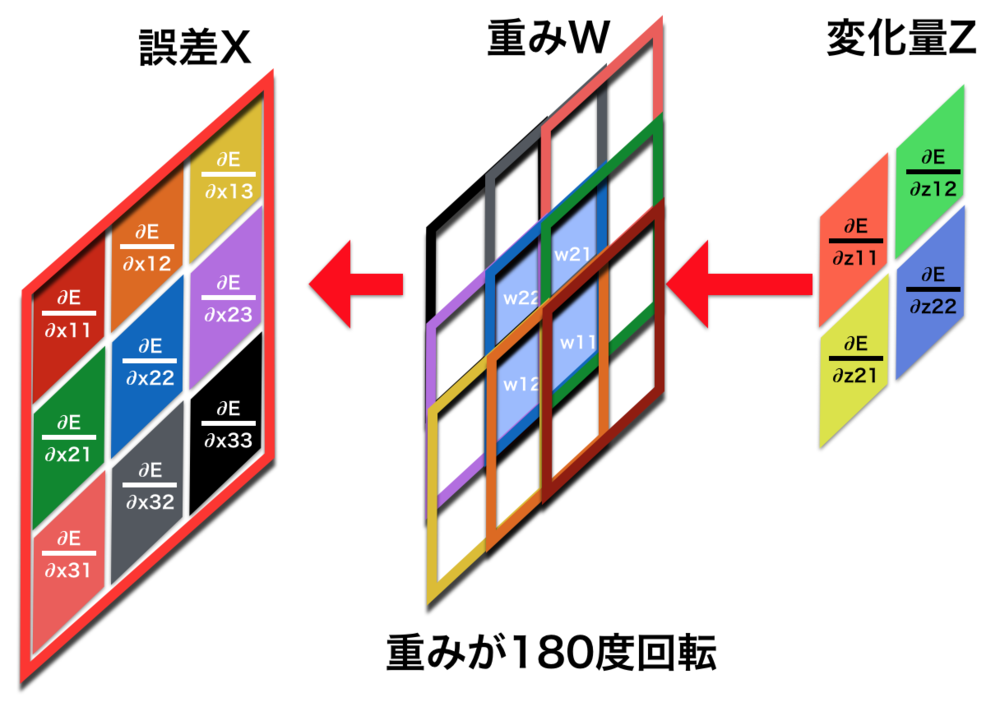 | 前の層に渡す誤差の更新 |
1.上の更新式の導出 | |
上記のような更新式は与えられている式と連鎖律(チェーンルール)から容易に導くことができる.
手順は
1. 順伝播の際の算出式を書き出し
2. それらを連鎖律によって更新式を求める | Convolution層の誤差逆伝播での更新式の導出 |
まずは順伝播のときの関係式を書き出します.
畳み込み層(Convolution)の場合は非常に簡単です.
入力,出力,重みをそれぞれ\(\boldsymbol{x},\boldsymbol{z},\boldsymbol{w} \)として、
それぞれ3x3, 2x2, 2x2としたときに、以下の計算を行なっている.
$$z_{11} = w_{11}x_{11} + w_{12}x_{12} + w_{21}x_{21} + w_{22}x_{22} \\
z_{12} = w_{11}x_{12} + w_{12}x_{13} + w_{21}x_{22} + w_{22}x_{23} \\
z_{21} = w_{11}x_{21} + w_{12}x_{22} + w_{21}x_{31} + w_{22}x_{32} \\
z_{22} = w_{11}x_{22} + w_{12}x_{23} + w_{21}x_{32} + w_{22}x_{33}
$$
これで順伝播の関係式は書き下せた. | まず順伝播のときの関係式 |
誤差逆伝播では後ろの層から\(\frac{\partial E}{\partial z}\)が得られるため、
これと\(x,w\)の値を使って、\(\frac{\partial E}{\partial w},\frac{\partial E}{\partial x}\)を求める. (先述したように\(\frac{\partial E}{\partial x}\)は次の層にとっての\(\frac{\partial E}{\partial z}\)となる)
パラメータの関係式の導出
連鎖律からまず以下のような式が書ける.
$$
\frac{\partial E}{\partial w_{11}} = \frac{\partial E}{\partial z_{11}}\frac{\partial z_{11}}{\partial w_{11}} +
\frac{\partial E}{\partial z_{12}}\frac{\partial z_{12}}{\partial w_{11}} +
\frac{\partial E}{\partial z_{21}}\frac{\partial z_{21}}{\partial w_{11}} +
\frac{\partial E}{\partial z_{22}}\frac{\partial z_{22}}{\partial w_{11}} \\
\frac{\partial E}{\partial w_{12}} = \frac{\partial E}{\partial z_{11}}\frac{\partial z_{11}}{\partial w_{12}} +
\frac{\partial E}{\partial z_{12}}\frac{\partial z_{12}}{\partial w_{12}} +
\frac{\partial E}{\partial z_{21}}\frac{\partial z_{21}}{\partial w_{12}} +
\frac{\partial E}{\partial z_{22}}\frac{\partial z_{22}}{\partial w_{12}} \\
\frac{\partial E}{\partial w_{21}} = \frac{\partial E}{\partial z_{11}}\frac{\partial z_{11}}{\partial w_{21}} +
\frac{\partial E}{\partial z_{12}}\frac{\partial z_{12}}{\partial w_{21}} +
\frac{\partial E}{\partial z_{21}}\frac{\partial z_{21}}{\partial w_{21}} +
\frac{\partial E}{\partial z_{22}}\frac{\partial z_{22}}{\partial w_{21}} \\
\frac{\partial E}{\partial w_{22}} = \frac{\partial E}{\partial z_{11}}\frac{\partial z_{11}}{\partial w_{22}} +
\frac{\partial E}{\partial z_{12}}\frac{\partial z_{12}}{\partial w_{22}} +
\frac{\partial E}{\partial z_{21}}\frac{\partial z_{21}}{\partial w_{22}} +
\frac{\partial E}{\partial z_{22}}\frac{\partial z_{22}}{\partial w_{22}} \\
$$
これと順伝播の式から実際に計算できるところを入れれば、
$$
\frac{\partial E}{\partial w_{11}} = \frac{\partial E}{\partial z_{11}}x_{11}+
\frac{\partial E}{\partial z_{12}}x_{12} +
\frac{\partial E}{\partial z_{21}}x_{21} +
\frac{\partial E}{\partial z_{22}}x_{22} \\
\frac{\partial E}{\partial w_{12}} = \frac{\partial E}{\partial z_{11}} x_{12} +
\frac{\partial E}{\partial z_{12}}x_{13} +
\frac{\partial E}{\partial z_{21}}x_{22} +
\frac{\partial E}{\partial z_{22}}x_{23} \\
\frac{\partial E}{\partial w_{21}} = \frac{\partial E}{\partial z_{11}}x_{21} +
\frac{\partial E}{\partial z_{12}}x_{22} +
\frac{\partial E}{\partial z_{21}}x_{31} +
\frac{\partial E}{\partial z_{22}}x_{32} \\
\frac{\partial E}{\partial w_{22}} = \frac{\partial E}{\partial z_{11}}x_{22} +
\frac{\partial E}{\partial z_{12}}x_{23} +
\frac{\partial E}{\partial z_{21}}x_{32} +
\frac{\partial E}{\partial z_{22}}x_{33}
$$
以上で求まった.
誤差の更新式の導出も上記と全く同じなのでここでは省略する. | 更新式を求める |
この章を学んで新たに学べる
Comments


