-
 @ThothChildren
@ThothChildren
- 2019.1.26
- PV 485
直線と放物線の面積算出の1/6公式
ー 概要 ー
直線と放物線で囲まれる面積を求める公式として1/6公式があります.計算を簡略化して計算ミスを減らすために使用されます.1/6公式を知らない採点官がいることもあるため、大学試験においては導出の途中で用いるときに完全に途中式をスキップするのは避けた方がよいかもしれません.
この章を学ぶ前に必要な知識
条件
- 放物線と直線で囲まれた面積を求める
効果
- 面積の計算において計算を簡単にすることができる
- y=ax^2+bx+cと直線で囲まれた面積は交点の座標をα,βとしてa*(α-β)^3/6
ポイント
- 放物線のaの係数のみ使用します
- 導出は容易
解 説
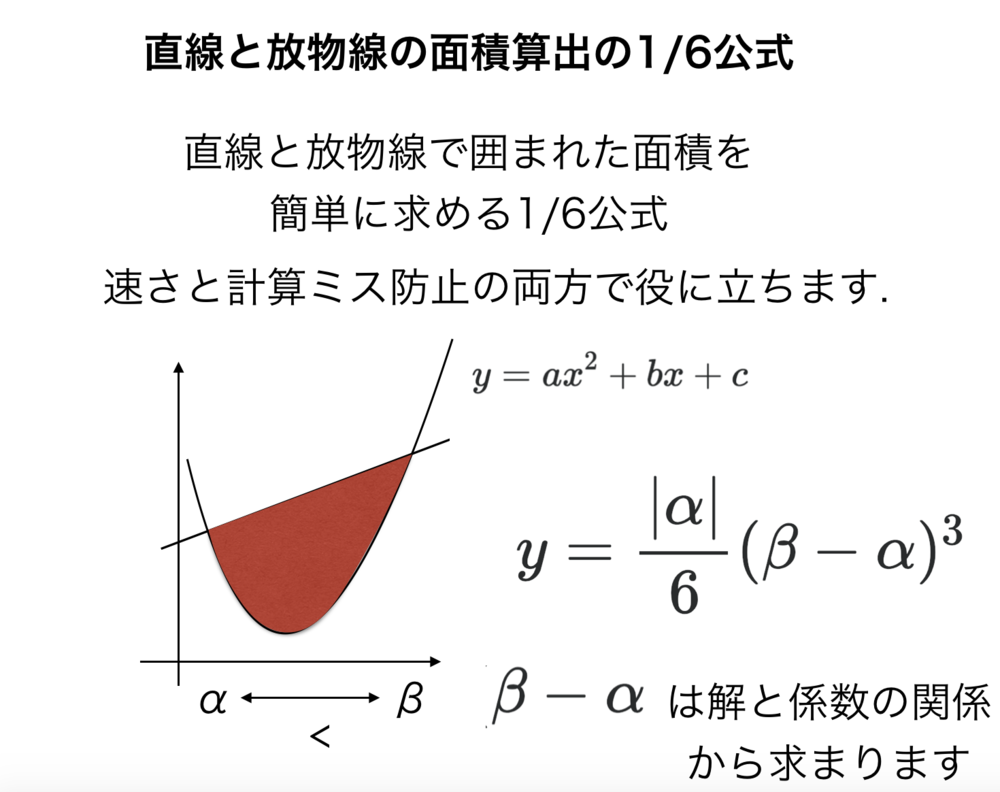
直線と放物線で囲まれる面積を求める公式として1/6公式があります.
計算を簡略化して計算ミスを減らすために使用されます.1/6公式を知らない採点官がいることもあるため、大学試験においては導出の途中で用いるときに完全に途中式をスキップするのは避けた方がよいかもしれません.(という話を聞いたことがあります.).念の為、この公式の導出を覚えておけば実際に計算をせずに途中式のみを提示することができます. | 直線と放物線の面積算出の1/6公式とは |
1/6公式についてまず紹介します.
直線
$$y=px+q$$
と
放物線
$$y=ax^2+bx+c$$
の交点を\(\alpha, \beta\)(\(\beta \gt \alpha \))とすると、
$$y = \frac{|a |}{6}(\beta-\alpha )^3$$ | 直線と放物線の面積算出の1/6公式 |
 | 概念図 |
1.1/6公式の導出 | |
$$y=ax^2+bx+c$$
の放物線とある直線\(y=px+q\) の解が\(\alpha, \beta(\beta \gt \alpha )\)とわかっているとき、求めたい面積は
$$y=a(x-\alpha)(x-\beta)$$
のx軸と放物線の囲む面積と同じになります.以下の図の通りです. | 解説しているサイトも多いですが
念の為導出しておきます. |
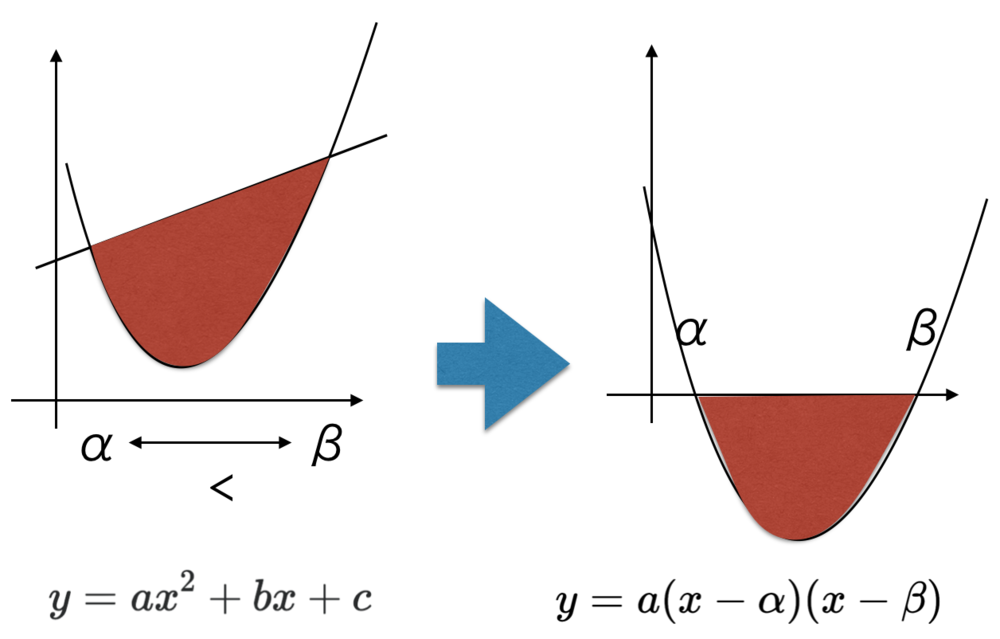 | y=ax^2+bx+cとy=px+qの間の面積はそれを引き算した、
y=a(x-α)(x-β)とx軸の間の面積を求めるのと同じこと |
上記の式を\(\alpha\)から\(\beta\)まで積分します.
$$\int_{\alpha}^\beta a(x-\alpha)(x-\beta)dx \\
= \int_{\alpha}^\beta a(x-\alpha)((x-\alpha) + (\alpha - \beta))dx \\
= a\int_{\alpha}^\beta ((x-\alpha)^2 - (\beta- \alpha )(x-\alpha))dx \\
= a\left[ \frac{ (x-\alpha )^3 }{ 3 } - (\beta - \alpha )\frac{(x-\alpha )^2 }{ 2 } \right]_{\alpha}^{\beta} \\
= -\frac{(\beta - \alpha )^3 }{6}
$$ | 導出まで |
2.β-αを求める | |
上記の公式によって式は簡易になりました.
しかしまだβ-αを求める必要があります.
β-αを求める方法は二つの方法がありそうです.
1. βとαをそれぞれ求めて引く
2. 解と係数の関係からα+βとαβでβーαを求める.
| β-αを求める |
1.は先ほどの方程式を求めるだけです.
$$y=ax^2 + (b-p)x+c-q = a(x-\alpha)(x-\beta )$$
の式から解の公式等を用いて、\(\alpha\)や\(\beta\)を求めます.
そしてそれらを使って\((\beta- \alpha) ^3 \)を求めます.
2.の場合は以下の関係を用います.
解と係数の関係から
$$-\frac{(b-p)}{a} = \alpha + \beta $$
$$\frac{(c-q)}{a} = \alpha \beta$$
が得られます.これは係数をそのまま使えばいいです.
次にこれらの値を使って、
$$(\beta-\alpha)^2 = (\alpha+\beta)^2 - 4\alpha\beta $$
から求めたい\((\beta - \alpha)^3 \)を算出できます. | (β-α)^3の算出 |
この章を学んで新たに学べる
Comments


