-
 @ThothChildren
@ThothChildren
- 2019.1.10
- PV 343
Log(Sum)をSum(Log)で扱いたい
ー 概要 ー
解析を行いにくいLog(Sum) (別表記log-sum)をSum(Log)(別表記lsum-log)の形に変形することで処理を扱いやすくすることが度々行われます.Log(Sum)からSum(Log)にして扱う時、イェンセンの不等式によってそれらを実現し、Log(Sum)>=Sum(Log)の関係となります.

この章を学ぶ前に必要な知識
条件
- Log(Sum)の形式で表される式
効果
- Log(Sum)>=Sum(Log)を導きSum(Log)で処理できるようにします
ポイント
- EMアルゴリズムにおいても扱いやすくするために上記処理が行われます.
解 説
以下で言うLog(Sum)とは
$$log(\Sigma q_i x_i )$$
のような形式で記述された関数を指し、
Sum(Log)とは
$$\Sigma q_i (log(f(x_i ))$$
のような形式で記述された関数を指すこととします. | 以下のLog(Sum), Sum(Log)とは |
解析を行いにくいLog(Sum)をSum(Log)の形に変形することで処理を扱いやすくすることが度々行われます.EMアルゴリズムやその他の情報理論において使用されます.
Log(Sum)を与えられたときに、イェンセンの不等式によって、Log(Sum)>=Sum(Log)の関係を導出します.
これによってSum(Log)はLog(Sum)より必ず小さい状態であるため、それを考慮した処理を行うことができます.
EMアルゴリズムでは、Log(Sum)で与えられる式は最大化を行いにくいため、その(変分)下限であるSum(Log)を求め、そのSum(Log)を大きくすることで、
Log(Sum)を最大化します. | Log(Sum)をSum(Log)で扱いたいとは |
イェンセンの不等式についてはリンクを参照願います. | イェンセンの不等式 |
以下が実際にイェンセンの不等式を当て込んだときの変形になります.
$$log(\Sigma q_i p_i(x)) \geqq \Sigma q_i (log(p_i(x)) )$$
条件として\(q_i\)の和は1になる必要があります.1でない場合はその和で割ればすぐに扱える形に変形できます. | イェンセン不等式による変換の例 |
1.Log-Sum 不等式 | |
またLog Sum不等式と呼ばれるイェンセンの不等式を使うことで容易に求められる不等式がある. | Log-Sum不等式について |
イェンセンの不等式で出てくる\(f(x)\)をここでは\(xlog(x)\)とする.\(log(x)\)は凹関数(上に凸な関数)だったが、この\(xlog(x)\)は凸関数(下に凸な関数)なので要注意.不等式の不等号の向きが逆転します.
$$a_{sum} = \Sigma a_i$$
$$b_{sum} = \Sigma b_i$$
です.
以下がlog-sum 不等式でこれから導く式になります.
$$\Sigma_{i=1}^n a_ilog\frac{a_i}{b_i} = a_{sum} log (\frac{a_{sum}}{b_{sum}} )$$
それでは導出です.
$$\Sigma_{i=1}^n a_ilog\frac{a_i}{b_i} = \Sigma_{i=1}^n b_i \frac{a_i}{b_i} log(\frac{a_i}{b_i}) = \Sigma_{i=1}^n b_i f(\frac{a_i}{b_i}) \\
= b_{sum} \Sigma_{i=1}^n \frac{b_i}{b_{sum}} f(\frac{a_i}{b_i}) \\
\geqq b_{sum} f(\Sigma_{i=1}^n \frac{b_i}{b_{sum}} \frac{a_i}{b_i})\\
= b_{sum} f(\frac{1}{b_{sum}} \Sigma_{i=1}^n {a_i})\\
= b_{sum} f(\frac{a_{sum}}{b_{sum}} ) \\
= a_{sum} log (\frac{a_{sum}}{b_{sum}} )
$$
以上です. 途中でイェンセンの不等式で変換をしているところを除きだいぶシンプルに導出できます. | log-sum不等式の導出 |
この章を学んで新たに学べる
Comments
Reasons
知識: イェンセンの不等式
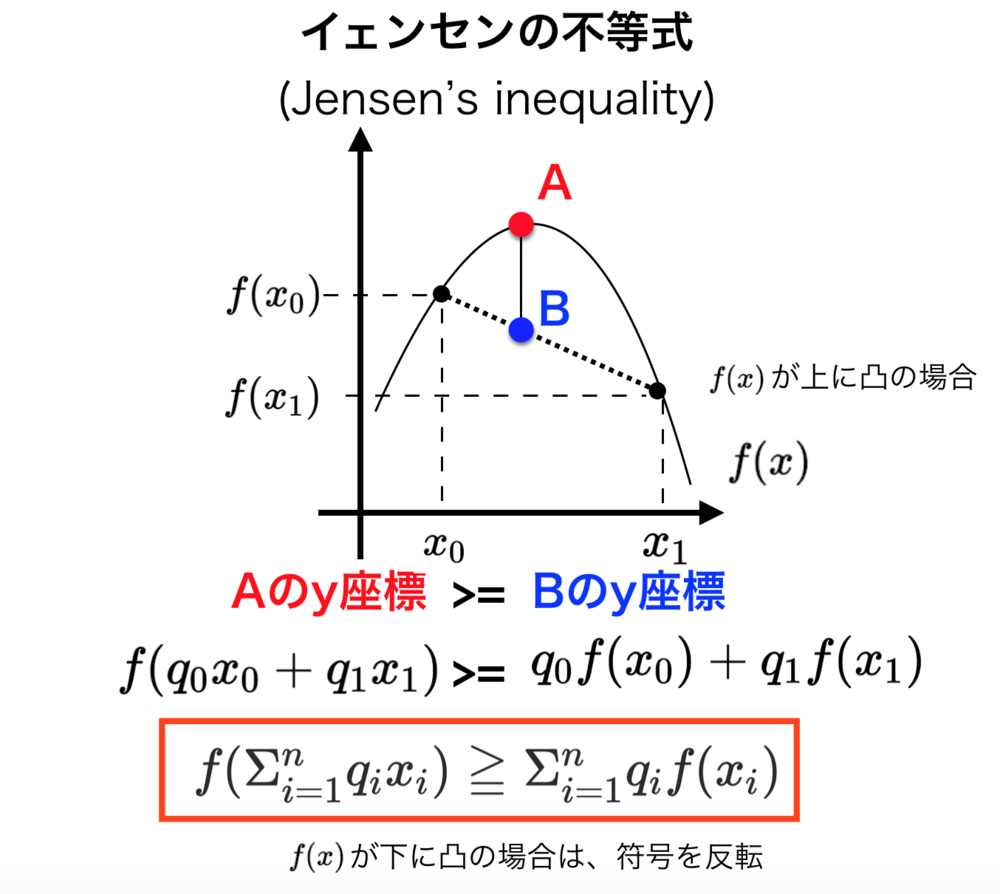
イェンセンの不等式(Jensen Inequality)とは、上に凸な関数f(x)とn個の変数x1~xnを使って表される不等式.全て足したら1となる係数q1~qnを使って、f(Σ(qi * xi)) >= Σ(qi * f(xi))が成立して、これをイェンセンの不等式と呼ぶ.


