-
 @ThothChildren
@ThothChildren
- 2019.1.26
- PV 203
微分のイメージ(高校数学)
ー 概要 ー
高校数学の基礎として習う微分について計算のイメージを持てていない方、微分が何をするものかわからない方のためにその計算のイメージを解説したページです.主に数学が苦手な人のための解説になるように書いています.あくまで曲線の微分をした時の説明になります.
この章を学ぶ前に必要な知識
条件
- 数学が苦手.傾きも不安な方用
効果
- 微分がどういう処理かわかる
ポイント
- どんな傾きかを求める式を計算するのが微分
解 説
微分について計算のイメージを持てていない方、微分が何をするものかわからない方のためにその計算のイメージを解説したページです.
しっかりとした数学というよりは、その初歩の概念を説明したものにすぎません. | 微分の基礎のイメージ(高校数学) |
1.まず傾き | |
まずは傾きのイメージです.
傾きは、以下の図のようにある直線や曲線がどの程度傾いているかを表します.
その傾きがわかるとこのあとその線は上がる方向を向いているのか下がる方向を向いているのかがわかったりします. | 傾きのイメージについて |
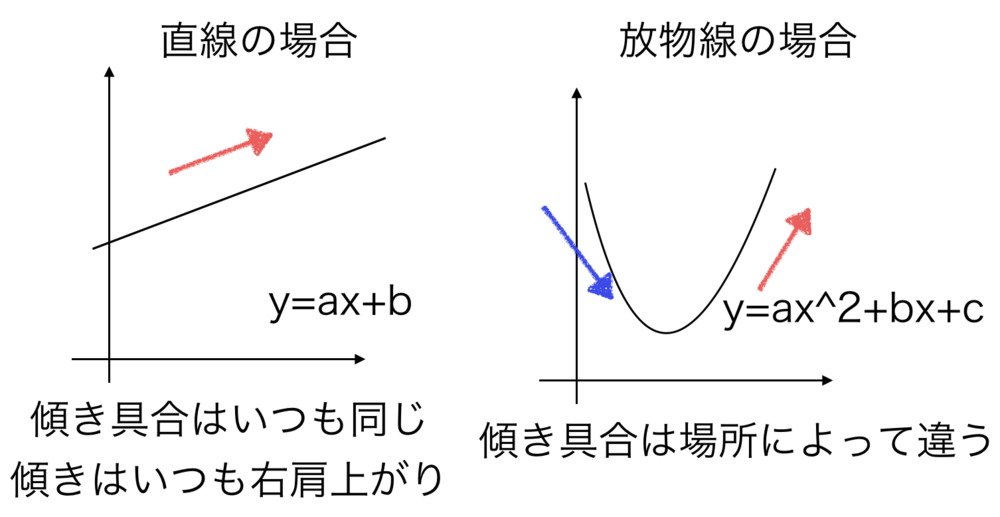 | 傾きのイメージ.
左の例では、
直線では傾きが常に上を向いているため、直線が右肩上がりになることがわかります.
放物線の場合は放物線の右側か左側かで傾きが大きく異なります.
右下方向に傾いている間は曲線が下に伸びていて、右上方向に傾いている間は曲線は上に伸びていってます. |
上で考えた傾きはすごく当たり前だったと思います.
図の傾きを見ればわかるじゃん!ってな感じでどんな傾きかがわかりました.
では、傾きを実際に計算で出すにはどうすればいいでしょうか?
すごく傾いているとかちょっと傾いているってどうやったら表せるでしょうか? | 傾きを計算するって |
正解は、「傾きはxを1動かしたときにyがどれだけ増えたり減ったりしたか」で表すです.
つまりほとんど傾いていないなら、x方向にちょっと移動した時にy方向にほとんど移動しないはずです.逆にすごく傾いているならx方向にちょっと移動しただけでy方向にも大きく移動することになります.
それを以下のように図にまとめました. | 傾きはxを1動かしたときにyがいくつ動いたかで表す. |
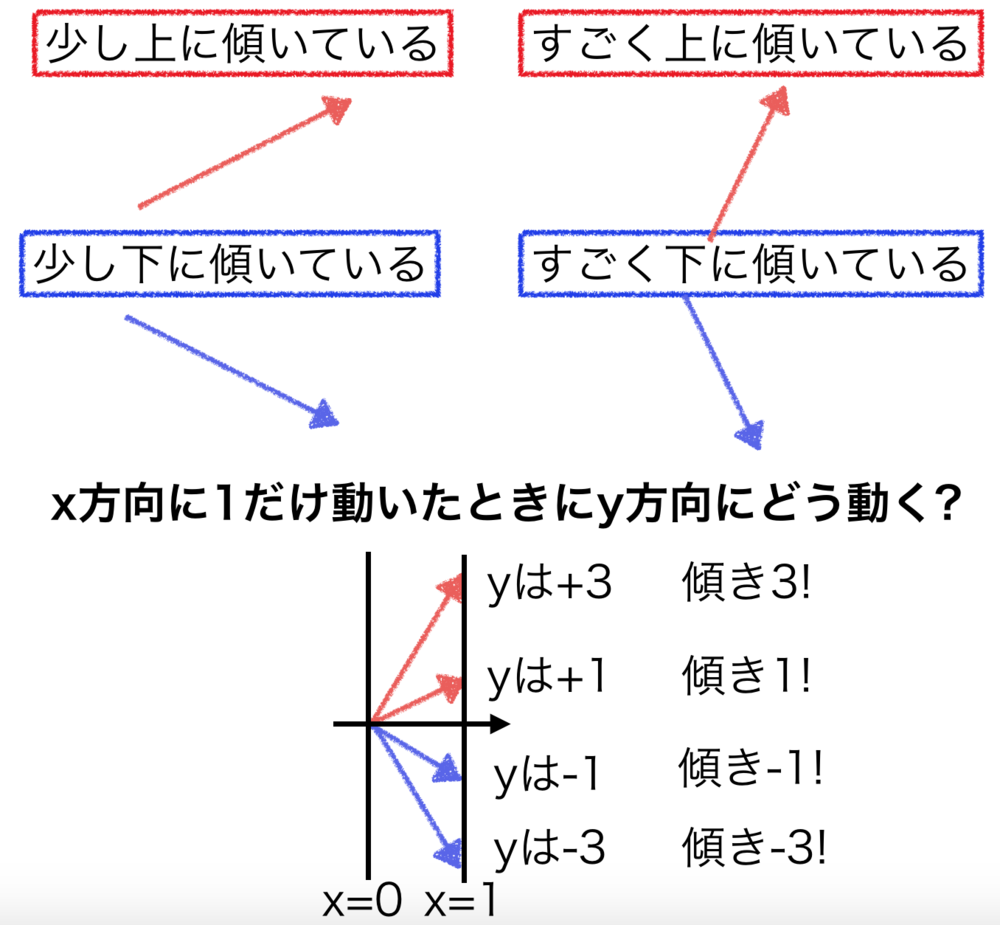 | 傾きの計算のイメージ |
それでは、実際に直線の場合に傾きを計算します.直線はわかりやすく\(y=x+1\)とします.
\(x\)はどこでもいいので例えば\(x=3\)だったとしましょう.
\(x=3\)のとき、\(y\)は
$$y = 4$$
一方で\(x=4\)のときには、
$$y = 5$$
となります.\(y\)は1増えているので、傾き1とわかります. | 直線の場合の傾きを計算する |
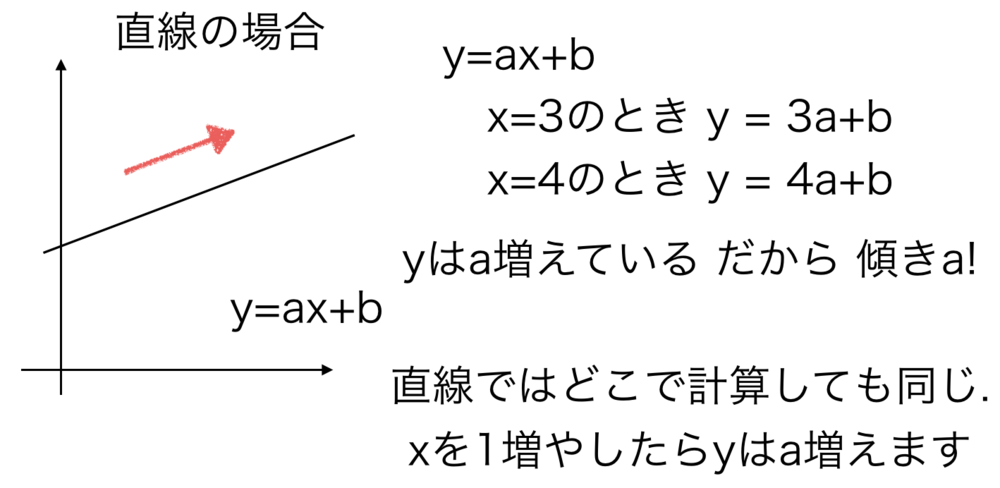 | y=ax+bの場合も書いておきます.
係数aが傾きと呼ばれるのはこのためです. |
ところで、xを1増やした時にyがどれくらい増えるかを考える時に
本当にxを1増やして計算する必要はありません.
傾きを計算したいのであれば、線上のある点aとある点bでのxの増え方とyの増え方から求めることができます.
xが5増えた時にyが5増えたなら、xが1増えたときにyも1増えているはずです.
つまりいつも「yが増えた分をxが増えた分で割れば傾き」ということが成り立つのが直感的にもわかるはずです.
xを本当に1増やした場合に割り算がなかったのは、割り算で1で割っても何も変わらないだけで実際には行なっているのと同じです. | xを1増やした時にyがどれくらい増えるか |
では、放物線の傾きはどう計算すべきでしょうか?
直線の場合はどこでも常に1の傾きだったりaの傾きだったりしましたが、
放物線の傾きはどこも一定ではなさそうです.
そこで微分を行います. | 放物線の傾き |
2.じゃ、微分 | |
それではいよいよ微分ですが、この先は非常に簡単です.
大事な事実は上に述べた通りです.
「xが増えた時にyがどれだけ増えたかが傾き」
「"微分"すると傾きがでる」
つまり"微分"の計算は、「xが増えた時にyがどれだけ増えたか」を求めるための処理です. | 微分の準備 |
それでは、放物線のときを考えます.
直線のときはどこでも傾きが同じだったためどこで求めても同じ傾きが得られましたが、
放物線の傾き具合はいつも変わってしまっています.
変わってしまうのはどうしようもありません.傾きはそれぞれの点で求めるしかないのです.
ではどうやってそれぞれの点で求めるのかという話について次に説明します. | 微分の計算って |
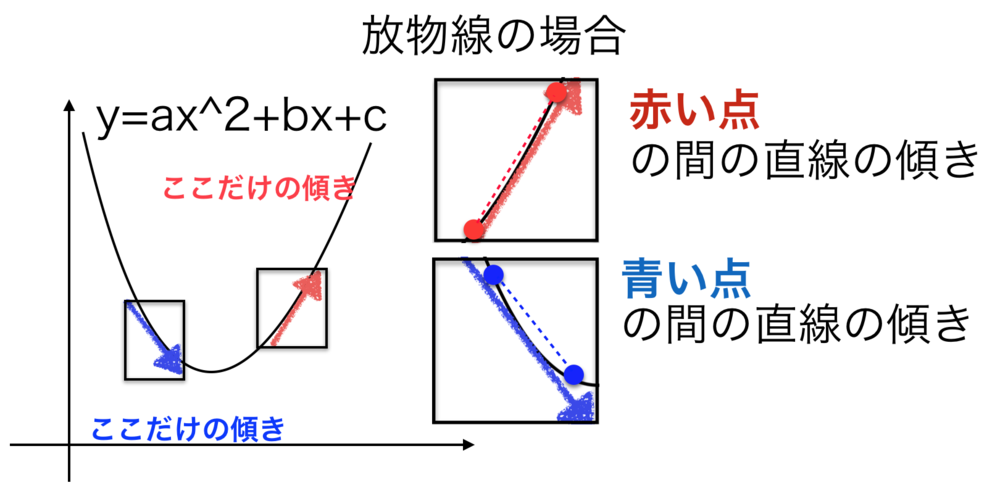 | 放物線の場合の傾きの出し方.
すごい近い二つの点の間の直線を求めると考えます.
赤い部分の傾きは赤い点の間
青い部分の傾きは青い点の間 |
さて、どのように求めるかは上の図で書いた通りです.
放物線もすごく小さい所に注目すれば、直線と同じです.
なので例えば赤い部分の傾きを求めたいならそのすごく小さい部分でxがちょっと動いたときにyがどれだけ増えたり減ったりしたかを求めれば放物線のそこでの傾きを求めたに等しいことになります.
例えば赤い部分の傾きを求めることにします.
$$y=ax^2+bx+c$$
の放物線で例えば\(x=p\)と\(x=p+q\)の間の傾きを求めることとしましょう.
\(q\)はすごく小さい値になるはずです.
\(y\)が増えた分は
$$(a(p+q)^2 + b (p+q)+c)-(ap^2 + bp+c) = 2apq + 2aq^2 + bq $$
\(x\)が増えた分は
$$(p+q)-p = q$$
つまり「yの変化分をxの変化分で割ったものが傾き」なので
傾きは
$$\frac{2apq + 2aq^2+bq}{q} = 2a(p+q)+b$$
となります.
これが傾きです!
と言われても実感がないかもしれません.しかし、二つの点の間の傾きは確かにこれで求まりました.あとは\(q\)が限りなく0に近ければ、0だと思えば(二つの点はすごく近いことになるので)、本当に\(x=p\)での傾きになります.
さっきの式で\(q=0\)とすると
$$2ap+b$$
となります.
この計算の流れが微分のやりたいことです.
| 放物線の傾きを求める |
上の式の
「二つの点の間の直線の傾きを求めて二つの点をめっちゃ近づけたら幾つになるか」
を計算しているのが微分です.
| 結局微分って |
上記を数式で書くと、教科書で見るような以下の式になります.
$$f'(p)=\lim_{q \to 0} \frac{f(p+q) -f(p)}{q}$$
この右側の式は、\(p\)での傾きを求めるために、yの変化量をxの変化量で割っていることがわかると思います.その後極限をとって(qを0にして)微分を求めます. | 微分を数式で書くと |
微分の基本とイメージは上記の通りです.
しかし、毎回上の計算をやるのはかなり大変です.
そのため有名な微分の公式として覚えれば使いまわすことができます.
例えば上で示した二次関数の微分は
$$y' = 2ax+b$$
で求めることができました.
これは実は\(x^{n}\) のときに微分したものは\(nx^{n-1}\)になるため、
$$y=ax^2+bx+c$$
を微分すると
$$y' = 2ax + b \times x ^ 0 + c \times 0 = 2ax+b $$
のように上のような計算を行わずに傾きを求める式を求められます.
微分の関係の公式はこのように幾らか覚えてしまえば、大抵の関数の微分をすることができます.
| 毎回極限をとるわけにはいかないので |
この章を学んで新たに学べる
Comments


