-
 @ThothChildren
@ThothChildren
- 2019.1.26
- PV 315
3次関数と接線の面積算出の1/12公式
ー 概要 ー
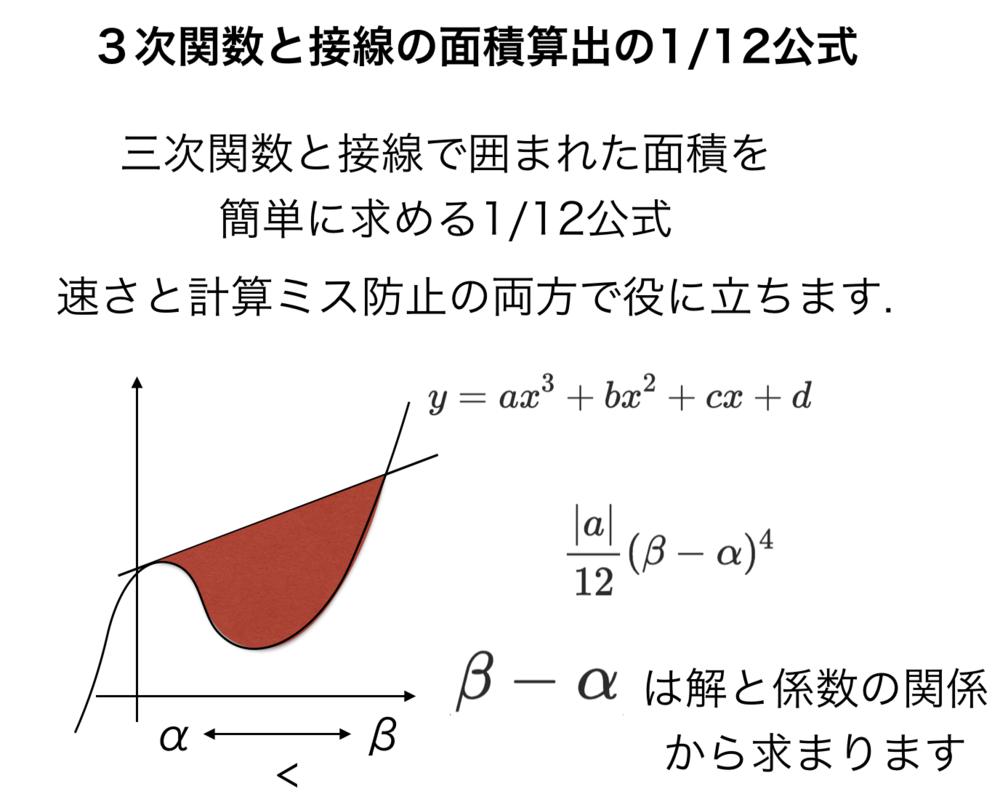
三次関数とその接線で囲まれる面積を求める公式として1/12公式があります.計算を簡略化して計算ミスを減らすために使用されます.1/12公式を知らない採点官がいることもあるため、大学試験においては導出の途中で用いるときに完全に途中式をスキップするのは避けた方がよいかもしれません.
この章を学ぶ前に必要な知識
条件
- 放物線と三次関数で囲まれた面積を求める
効果
- 面積の計算において計算を簡単にすることができる
- y=ax^3+bx^2+cx+dと接線で囲まれた面積は交点の座標をα,βとしてa*(α-β)^4/12
ポイント
- 放物線のaの係数のみ使用します
解 説
この章を学んで新たに学べる
Comments
Reasons
知識: 直線と放物線の面積算出の1/6公式
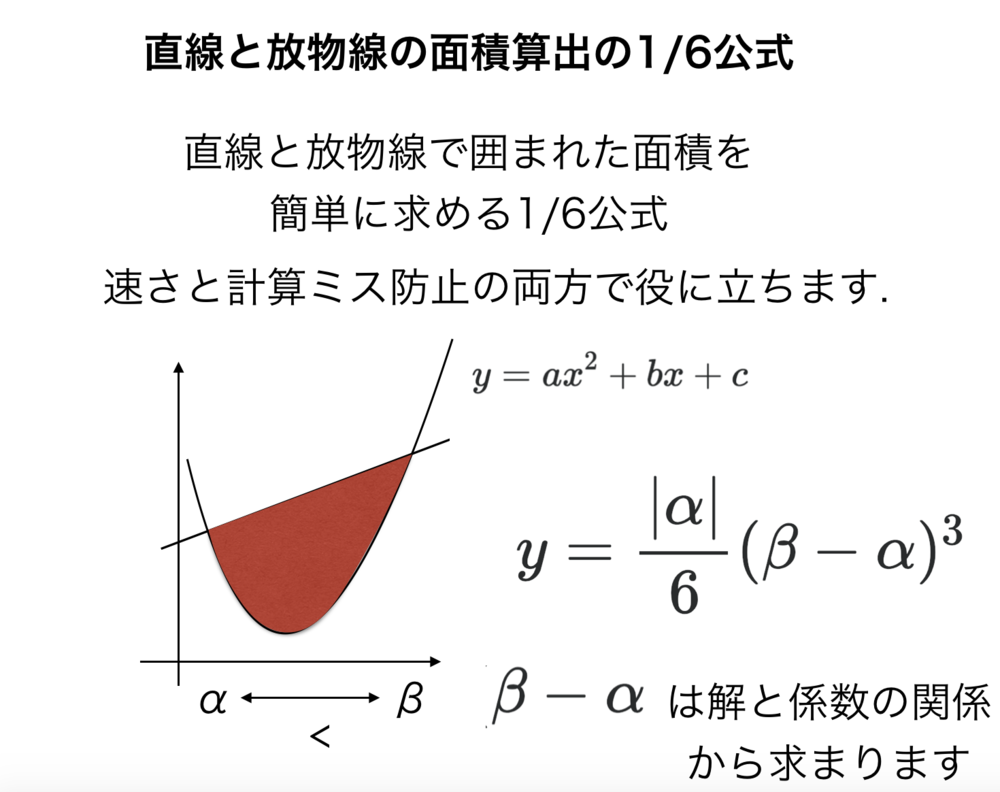
直線と放物線で囲まれる面積を求める公式として1/6公式があります.計算を簡略化して計算ミスを減らすために使用されます.1/6公式を知らない採点官がいることもあるため、大学試験においては導出の途中で用いるときに完全に途中式をスキップするのは避けた方がよいかもしれません.


