©2025 Thoth Children All rights reserved.

イェンセンの不等式

ー 概要 ー

イェンセンの不等式(Jensen Inequality)とは、上に凸な関数f(x)とn個の変数x1~xnを使って表される不等式.全て足したら1となる係数q1~qnを使って、f(Σ(qi * xi)) >= Σ(qi * f(xi))が成立して、これをイェンセンの不等式と呼ぶ.
Facebookシェア Twitterツイート LINEで送る このエントリーをはてなブックマークに追加
この章を学ぶ前に必要な知識
0
条件
  • 係数は足して1にならなくてはならない
  • f''(x)が全実数で0以下(上に凸の関数の場合),0以上(下に凸の関数の場合)
効果
  • f(Σ(qi * xi)) >= Σ(qi * f(xi))が成立
ポイント
  • 係数の合計を1にするためには式をそのような係数になるように逆数で割ったりすることで調整
  • EMアルゴリズムなど重要なアルゴリズムで用いられる不等式
  • 凹関数(上に凸な関数)であるlogがfとして用いられることがあり、頻繁にLog(Σ)の形を扱いやすいΣ(Log)に変えるために使用
  • 下に凸な関数では不等号を反転

解 説

イェンセンの不等式(Jensen Inequality)とは、上に凸な関数f(x)とn個の変数x1~xnを使って表される不等式.全て足したら1となる係数q1~qnを使って、以下のような不等式が成り立ち、これをイェンセンの不等式と呼ぶ.
イェンセンの不等式とは
$$ f(\Sigma_{i=1}^{n} q_i x_i )\geqq \Sigma_{i=1}^{n} q_i f(x_i)$$
イェンセンの不等式 (上に凸な関数: 凹関数(今回はこちら). 下に凸な関数:凸関数でも符号を反転させれば同様に成立)
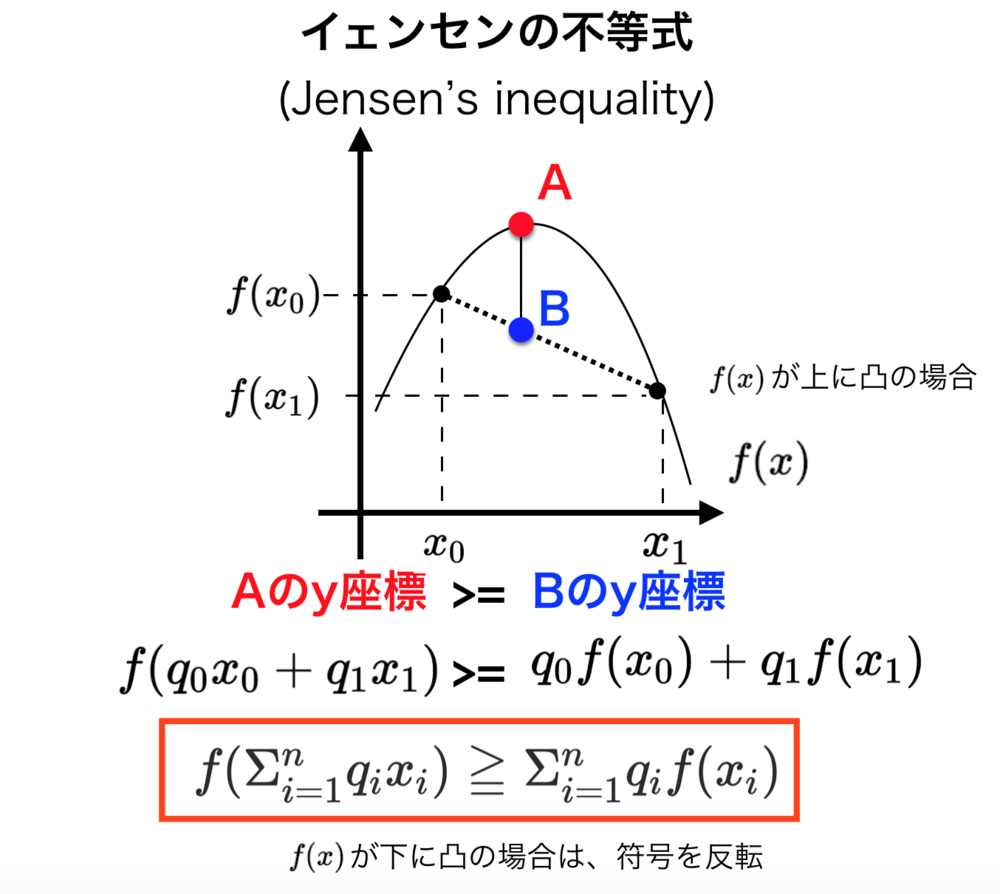
イェンセンの不等式は、上に凸な関数(下に凸な関数でもよい)を考えれば自然と理解することができる. 下図のようにf(x)があったとする.ここで変数が2点のみとした場合を考える. 上記不等式の左辺は\(q_0 + q_1 = 1\)となるような\(x_0,x_1\)の内分点を求めてその座標での\(f(x)\)の値を求めている.すなわち図の点Aのy座標を求めている計算となる. 一方で、 上記不等式の右辺は\(f(x_0),f(x_1)\)の値を\(q_0 + q_1 = 1\)となるような比率でy座標の内分点を求めている.すなわち図の点Bのy座標を求めている計算となる. 図からわかるように上に凸な関数においては必ず(点Aのy座標)>=(点Bのy座標)は成立することがわかる.これがイェンセンの不等式の示すところ.
イェンセンの不等式の直感的理解
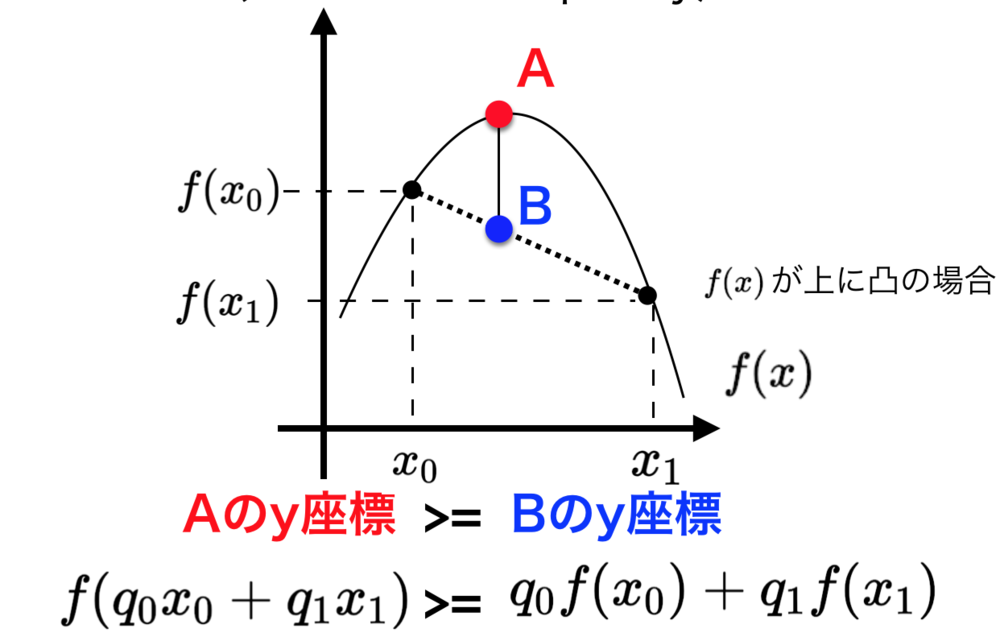xが2変数で、f(x)が凹関数(上に凸)の場合.
この章を学んで新たに学べる
Comments

Reasons
>>隠す