万有引力による位置エネルギー

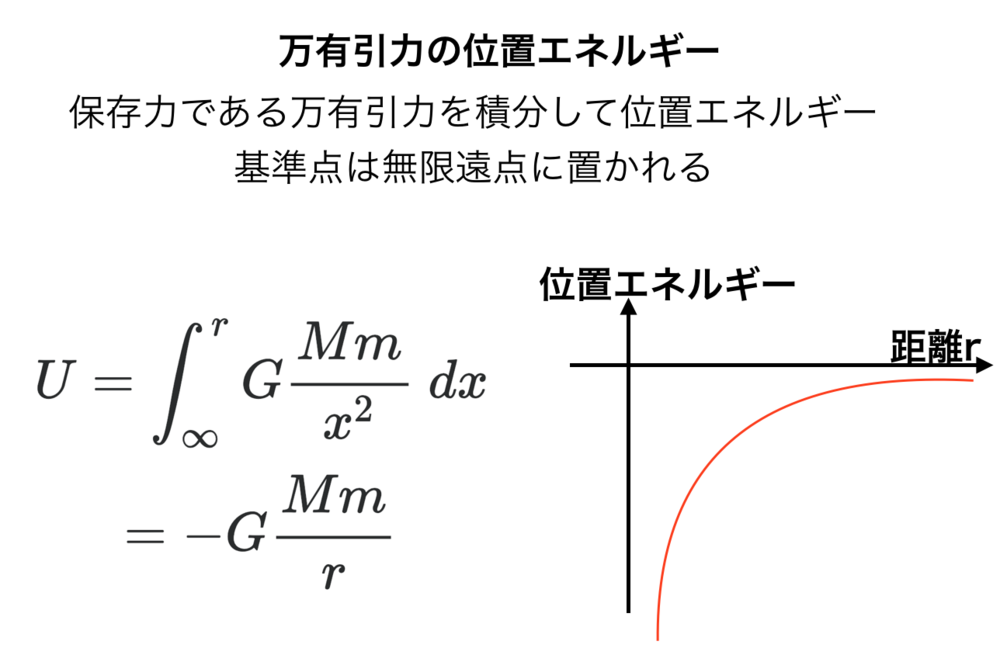
保存力である万有引力があることによって定義することができる位置エネルギーについてまとめています.負の方向に無限大になるため、基準を無限遠点になるようにするのが一般的です.位置エネルギーは万有引力を積分することで得られます. 万有引力の式は以下で与えられます. $$F= G\frac{Mm}{r^2 }$$ 通常の位置エネルギーは $$U = \int_0^h mg \ dx = mgh$$ であったように万有引力の位置エネルギーにおいては、 $$U = \int_{\infty}^r G\frac{Mm}{x^2 } \ dx \\ = -G\frac{Mm }{r} $$ で導出できます.

上記の式の $$U=-G\frac{Mm}{r}$$ からわかるように\(r=0\)で負の方向に無限,\(r=\infty\)のときに0になることがわかります. \(mgh\)の位置エネルギーはどこを基準にしても良かったように、万有引力による位置エネルギーもどこを0基準にするかは自由に決めることができます. 負の方向に無限に伸びている部分はどこを基準にするかが難しいため、無限遠点で0になる性質を利用して、0を基準とすることで扱いやすくしています. もし仮に無限遠で停止していたとするとその状態は\(U=0\)で運動エネルギーも0ということになります. それを距離\(r\)のところまで移動させたのであれば、 $$E = -G\frac{mM}{r} + \frac{1}{2}mv^2 = 0 + 0 $$ となります.