解析学
微分、積分、収束、集合、極限、確率等を含む学問分野.
2017.10.13
-
143Views
-
0Watch
-
10Knows
|
|
解析学の新規投稿
ガウス過程
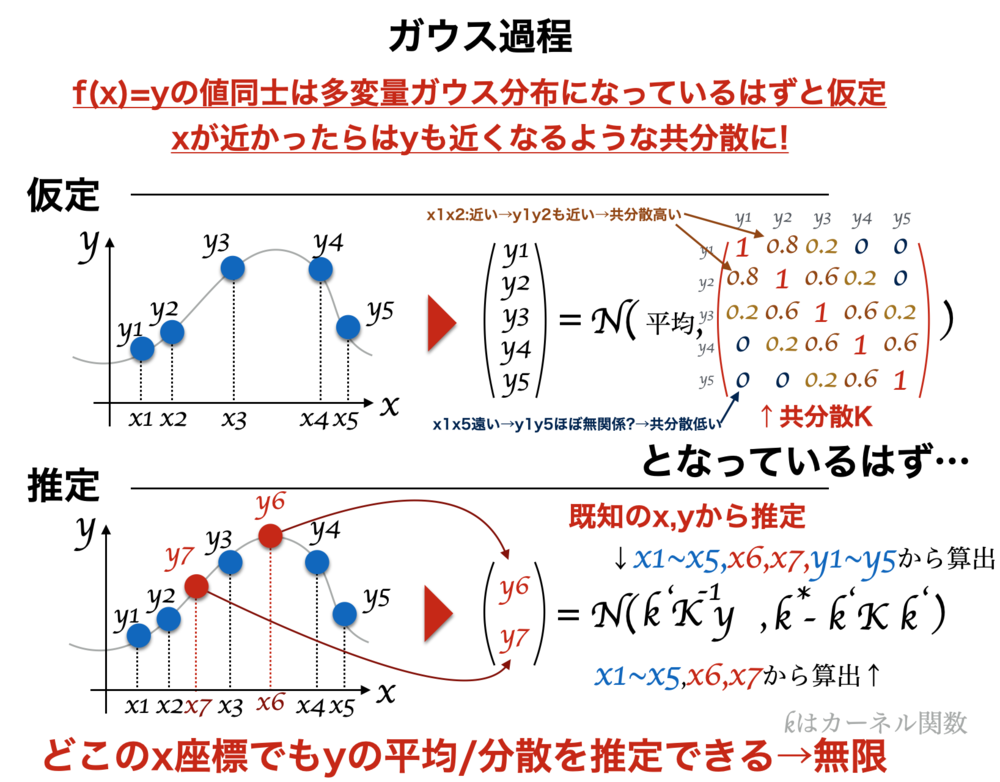
複数の入力に対応した出力値がガウス分布(正規分布)に従う確率過程であるときガウス過程と呼ぶ. 「xの値が近いときにyの値が近い」というのを分散共分散行列で表現. 回帰として使えば、分かっているデータから他のx座標に対応したy座標の平均と座標を推定可能. この記事ではこの回帰を行う場合について簡単に解説する.
PV 1044
Fav 0
2020.08.29

連鎖律(チェーンルール)
連鎖律(チェーンルール)は多変数の合成関数の微分において成立する関係式です.合成関数の導関数は各々の関数の微分、偏微分の積で求めることができます.様々な場面で使用される有用な手法です.
PV 1176
Fav 0
2019.01.28

ギブスの不等式
ギブスの不等式は、二つの確率分布の間に成立する不等式.この不等式をどちらかにまとめたものはカルバック・ライブラー情報量に等しく、カルバック・ライブラー情報量が常に0以上であることを示す式を得られる.
PV 382
Fav 0
2019.01.10
イェンセンの不等式
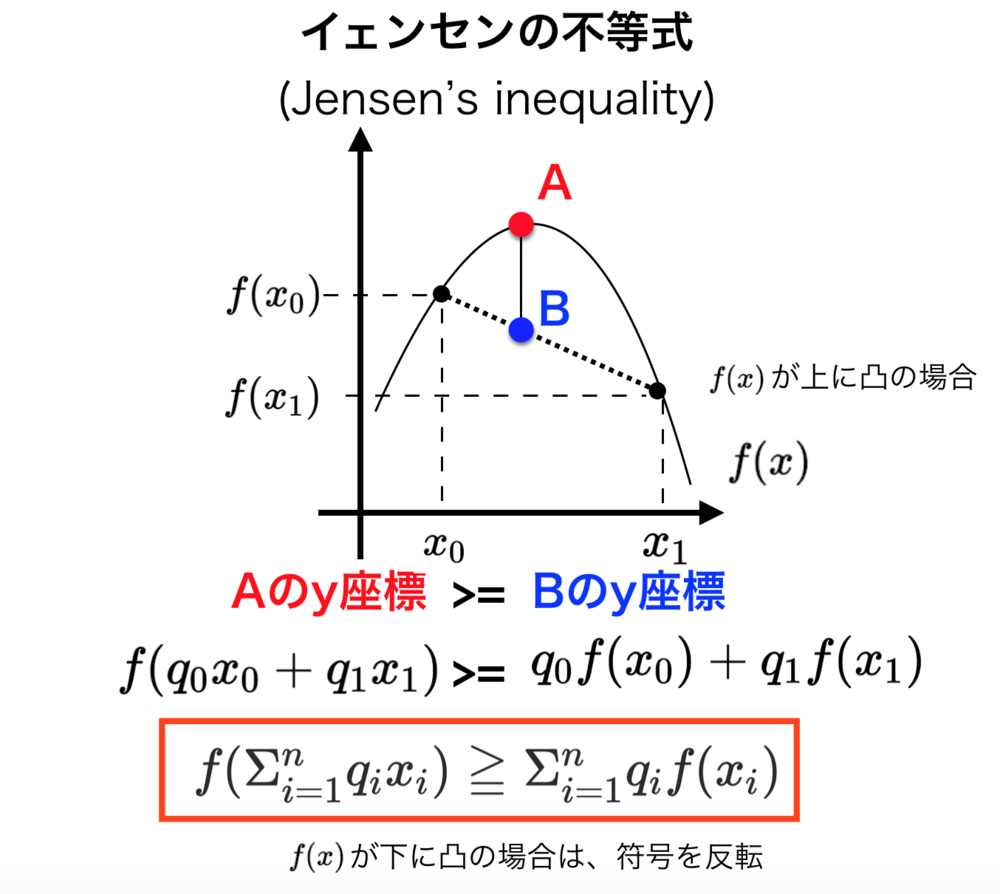
イェンセンの不等式(Jensen Inequality)とは、上に凸な関数f(x)とn個の変数x1~xnを使って表される不等式.全て足したら1となる係数q1~qnを使って、f(Σ(qi * xi)) >= Σ(qi * f(xi))が成立して、これをイェンセンの不等式と呼ぶ.
PV 438
Fav 0
2019.01.10

L-System
L-System(Lindenmayer system)は、初期の文字列と文字置き換え規則によってできる文字列置き換えシステムまたは形式文法のことを指す.初期は、植物の成長のモデルの表記方法として提案されていたが、有名なドラゴン曲線などのフラクタルの表現を行うことができる
PV 204
Fav 0
2018.11.04

ペアノ曲線
ペアノ曲線(Peano Curve)は、一次元の値域を単位正方形(n次元でも可)に往復する形で対応させて実現したフラクタルな空間充填曲線.空間充填曲線を一般的に指す時もある.
PV 372
Fav 0
2018.10.24

Z-order 曲線(Z階数曲線)
Z-Order 曲線は、ルベーグ曲線、 モートン階数 あるいは モートン符号 とも呼ばれる平面や空間をz型に移動しながら全ての単位正方形、単位立方体を通る空間充填曲線の一つ.ヒルベルト曲線より位置関係の保持する性能は劣る.
PV 283
Fav 0
2018.10.23
ヒルベルト曲線
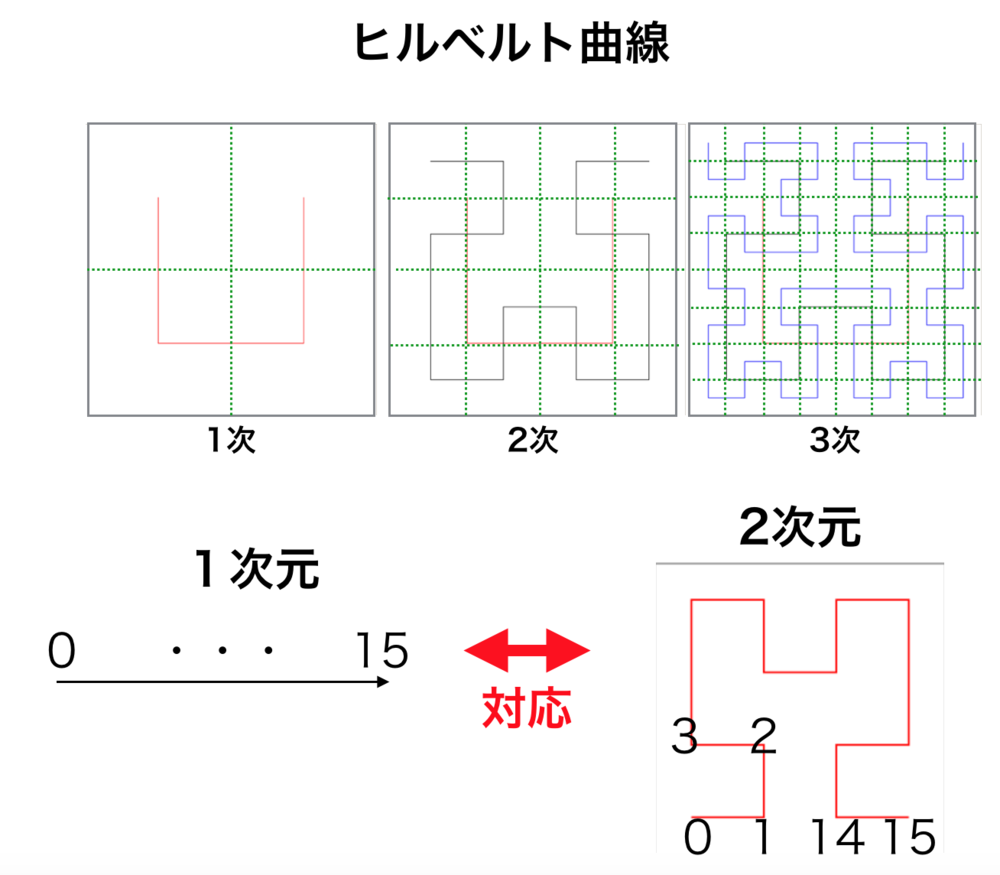
ヒルベルト曲線(Hilbert Curve)は、平面や空間内の単位正方形、単位立方体を特定のパターンに乗っ取って全て通るフラクタルな空間補充曲線の一つ.(一本の線で全部のブロックを通るようにする)他の空間充填曲線によってマッピングを行うよりもより位置関係を保持する曲線になっている.応用例も多く、空間インデックスや検索、などがある.1次元の値がn次元に対応しているため、原点からの距離が近いとその空間でも近いとわかる.
PV 543
Fav 0
2018.10.23
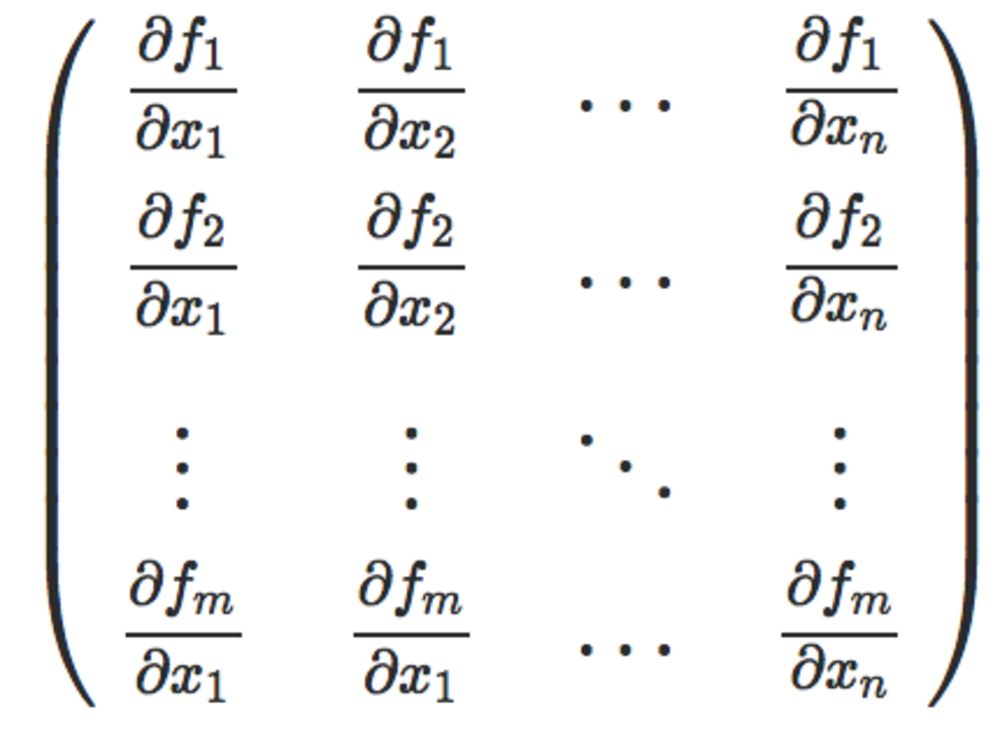
ヤコビ行列
多変数関数を入力として多変数ベクトルを出力する関数fを入力の変数で一回微分して行列に整理したものをヤコビ行列と呼ぶ.またヤコビ行列の行列式をヤコビアンと呼ぶ.ロボットの関節角を求める計算などの最適化計算などにおいて用いられる.
PV 429
Fav 0
2018.07.07
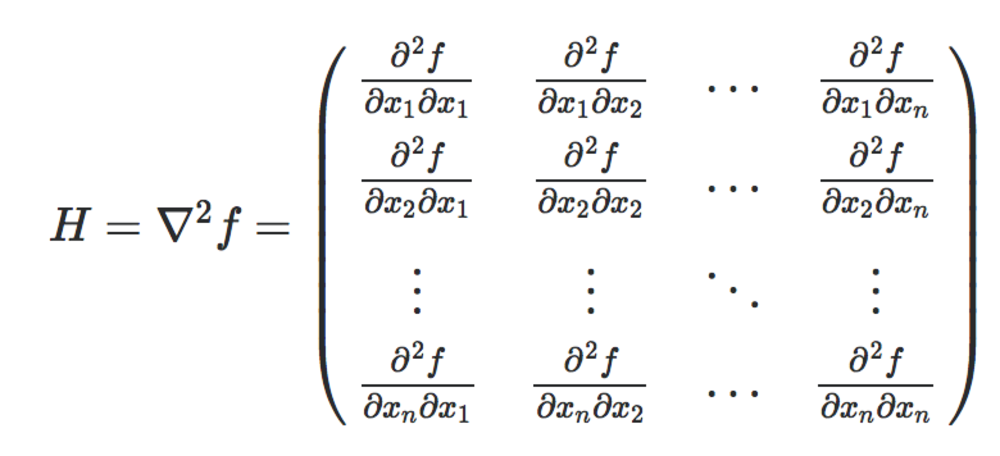
ヘッセ行列
多変数関数f(x_1, x_2, x_3....)のような関数を各x_1, x_2...で二階微分を行い行列としたものをヘッセ行列という.極値の判定やニュートン法における近似解導出に用いられる
PV 1274
Fav 0
2018.07.07
解析学人気知識・質問
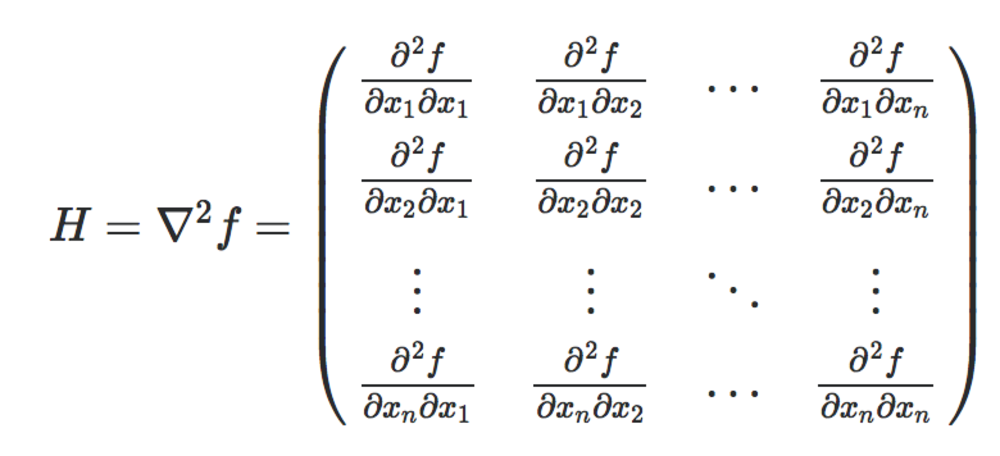
ヘッセ行列
多変数関数f(x_1, x_2, x_3....)のような関数を各x_1, x_2...で二階微分を行い行列としたものをヘッセ行列という.極値の判定やニュートン法における近似解導出に用いられる
PV 1274
Fav 0
2018.07.07

連鎖律(チェーンルール)
連鎖律(チェーンルール)は多変数の合成関数の微分において成立する関係式です.合成関数の導関数は各々の関数の微分、偏微分の積で求めることができます.様々な場面で使用される有用な手法です.
PV 1176
Fav 0
2019.01.28

ガウス過程
複数の入力に対応した出力値がガウス分布(正規分布)に従う確率過程であるときガウス過程と呼ぶ. 「xの値が近いときにyの値が近い」というのを分散共分散行列で表現. 回帰として使えば、分かっているデータから他のx座標に対応したy座標の平均と座標を推定可能. この記事ではこの回帰を行う場合について簡単に解説する.
PV 1044
Fav 0
2020.08.29

ヒルベルト曲線
ヒルベルト曲線(Hilbert Curve)は、平面や空間内の単位正方形、単位立方体を特定のパターンに乗っ取って全て通るフラクタルな空間補充曲線の一つ.(一本の線で全部のブロックを通るようにする)他の空間充填曲線によってマッピングを行うよりもより位置関係を保持する曲線になっている.応用例も多く、空間インデックスや検索、などがある.1次元の値がn次元に対応しているため、原点からの距離が近いとその空間でも近いとわかる.
PV 543
Fav 0
2018.10.23

イェンセンの不等式
イェンセンの不等式(Jensen Inequality)とは、上に凸な関数f(x)とn個の変数x1~xnを使って表される不等式.全て足したら1となる係数q1~qnを使って、f(Σ(qi * xi)) >= Σ(qi * f(xi))が成立して、これをイェンセンの不等式と呼ぶ.
PV 438
Fav 0
2019.01.10
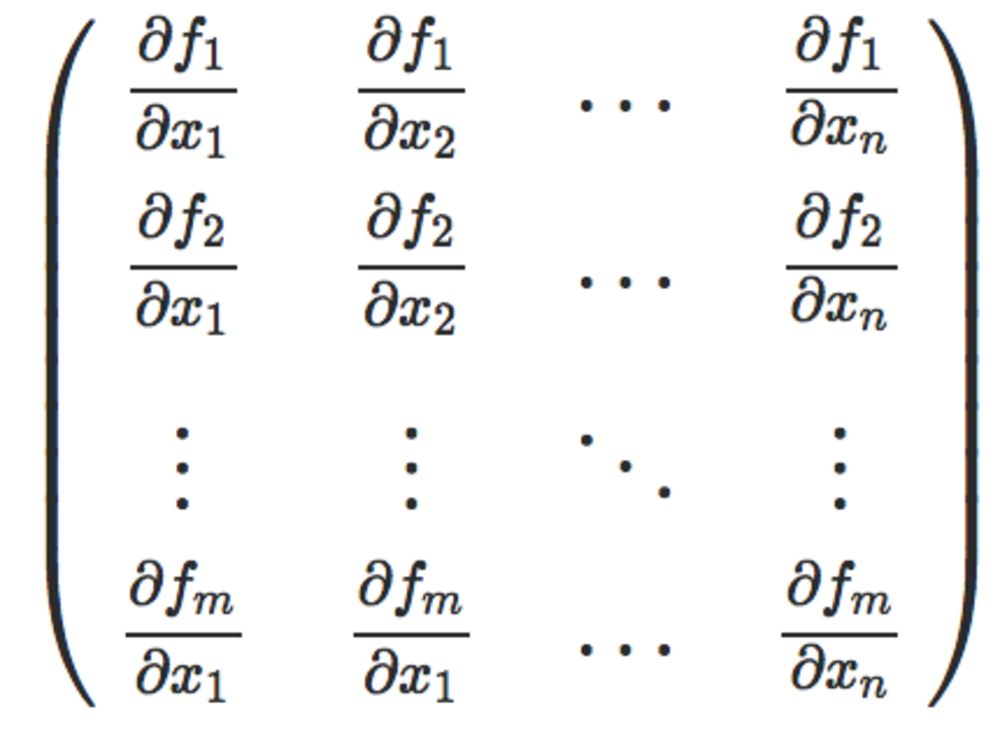
ヤコビ行列
多変数関数を入力として多変数ベクトルを出力する関数fを入力の変数で一回微分して行列に整理したものをヤコビ行列と呼ぶ.またヤコビ行列の行列式をヤコビアンと呼ぶ.ロボットの関節角を求める計算などの最適化計算などにおいて用いられる.
PV 429
Fav 0
2018.07.07

ギブスの不等式
ギブスの不等式は、二つの確率分布の間に成立する不等式.この不等式をどちらかにまとめたものはカルバック・ライブラー情報量に等しく、カルバック・ライブラー情報量が常に0以上であることを示す式を得られる.
PV 382
Fav 0
2019.01.10

ペアノ曲線
ペアノ曲線(Peano Curve)は、一次元の値域を単位正方形(n次元でも可)に往復する形で対応させて実現したフラクタルな空間充填曲線.空間充填曲線を一般的に指す時もある.
PV 372
Fav 0
2018.10.24

Z-order 曲線(Z階数曲線)
Z-Order 曲線は、ルベーグ曲線、 モートン階数 あるいは モートン符号 とも呼ばれる平面や空間をz型に移動しながら全ての単位正方形、単位立方体を通る空間充填曲線の一つ.ヒルベルト曲線より位置関係の保持する性能は劣る.
PV 283
Fav 0
2018.10.23

L-System
L-System(Lindenmayer system)は、初期の文字列と文字置き換え規則によってできる文字列置き換えシステムまたは形式文法のことを指す.初期は、植物の成長のモデルの表記方法として提案されていたが、有名なドラゴン曲線などのフラクタルの表現を行うことができる
PV 204
Fav 0
2018.11.04