-
 @ThothChildren
@ThothChildren
- 2020.8.29
- PV 1045
ガウス過程
ー 概要 ー
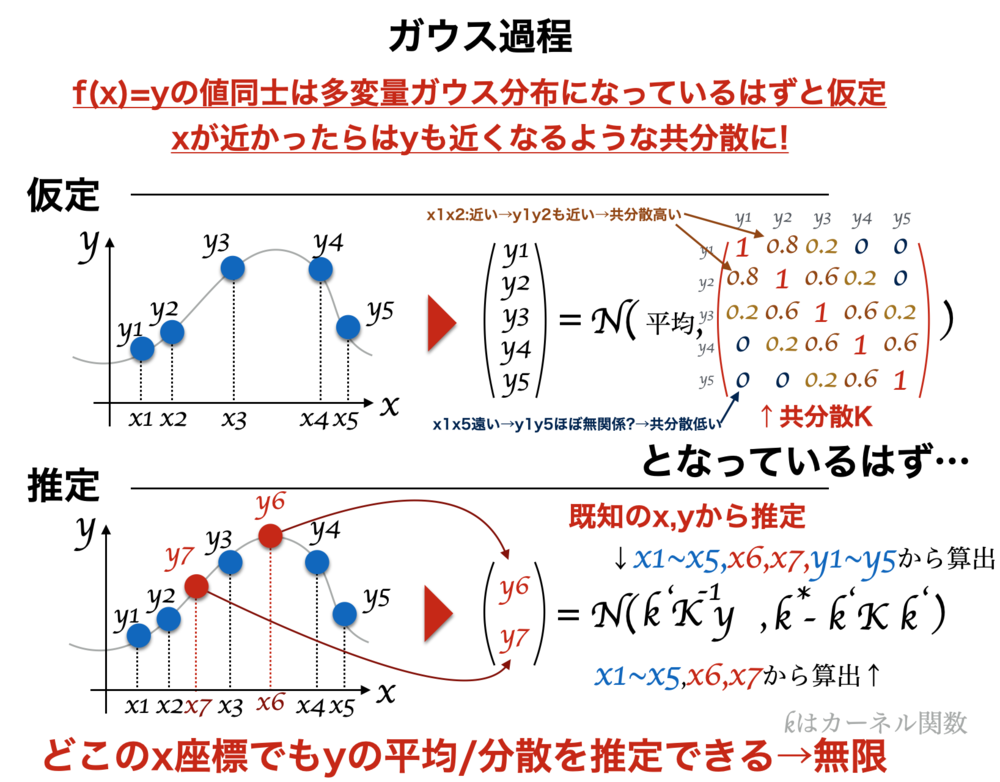
複数の入力に対応した出力値がガウス分布(正規分布)に従う確率過程であるときガウス過程と呼ぶ. 「xの値が近いときにyの値が近い」というのを分散共分散行列で表現. 回帰として使えば、分かっているデータから他のx座標に対応したy座標の平均と座標を推定可能. この記事ではこの回帰を行う場合について簡単に解説する.
この章を学ぶ前に必要な知識
条件
- y座標が多変量ガウス分布に従うと仮定
- 二つのx座標で計算するカーネル関数をあらかじめ選んどく
効果
- 任意のx座標に対応するy座標の平均と分散を推定
- ノイズが乗っている場合も考慮して算出
ポイント
- 事前に学習は不要. その場で計算
- 分散共分散行列の要素は各x座標の組み合わせをカーネル関数で計算
- データ点数Nが増えると、計算量もN^3に比例
解 説
ガウス過程のわかりやすい解説 | |
ガウス過程の概要について簡単にまとめる.ここではガウス過程で回帰を行う場合について述べる.
ガウス過程の回帰のポイント
・各y座標の値はガウス分布になっていて、x座標の異なるy座標同士も関係するのでそのガウス分布の平均や分散も他の値に影響される(多変量ガウス分布)と仮定.
・推定したいx座標とデータの分散共分散行列を計算するのが主な処理.その値から、平均と分散を算出
・\(n\)個の\(y\)の値(\(p(\boldsymbol{ y })\))が分散共分散行列\(\Sigma \)の\(n\)次元の多変量ガウス分布になっていると想定
→\(d\)個の変数の値がデータとして得られた
→じゃ残りの\((n-d)\)個のガウス分布(\(p(\boldsymbol{ y_{n-d} }|y_1\cdots y_d)\))は?
という流れ
ガウス過程の欠点
愚直に行うと全てのデータ(N個)とx座標の組み合わせを計算したり、NxNの行列を計算するため、Nが大きいとてつもない計算量になる.
| ガウス過程の概要 |
1.ガウス過程と多変量ガウス分布 | |
ガウス過程は、「N個の\((x,y)\)のデータの\(y\)が多変量ガウス分布に従っている」と想定しているが、それはどういうことで、どう使われていくのかについて解説していく.
まずは理解することを優先して、
ガウス過程による回帰はぬるぬる関数を確率的にぽんと出す何かではなく、推定したい座標の平均と分散を出すイメージ
と考えて以下を読み進めてください. | ガウス過程と多変量ガウス分布 |
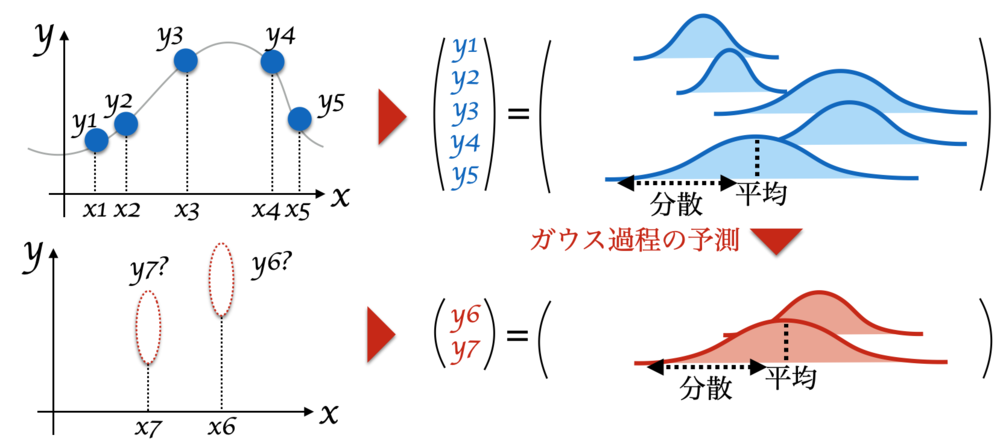 | データx,yはベクトルで表記.
データx,yを使って
予測/推定したいx座標の平均と分散を求めるイメージ |
1.1.多変量ガウス分布で値を推定する | |
簡単のため、1個だけデータ\(y_0\)があり、1つだけ\(y_t\)推定したいとする.
前提
\(y_0\)の値は10
推定したい\(y_t\)の平均\(\mu_t\)も分散\(\sigma_t\)も分からない.
でも\(y_0, y_t\)がどんな分布になるか分かっていて、それは多変量ガウス分布.
この前提のとき、\(y_t\)の値を求めるのは非常に簡単で、以下のような図のようにもとまる.
| 1つのデータと1つの推定したい座標があるときで
ガウス分布の処理を考える |
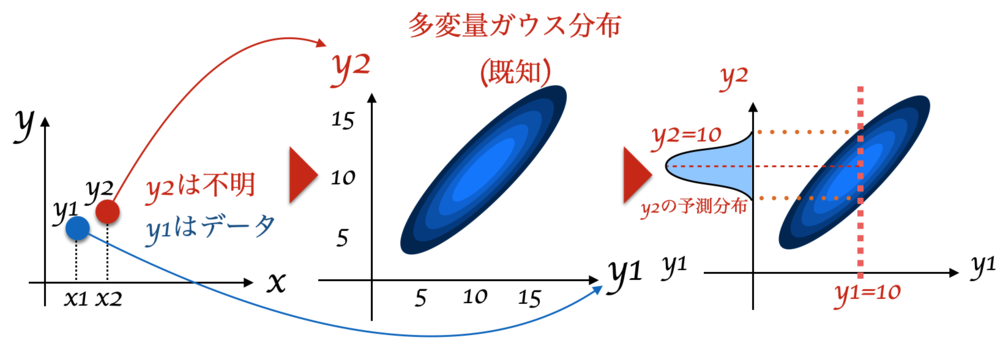 | y0からytの分布を求める.
多変量ガウス分布と分かっているためytの分布が予想できる. |
上記のように\(y_t\)(上図では\(y_2\))は、多変量ガウス分布で\(y_0\)が既知のため、簡単に求めることができた. 多変量ガウス分布と仮定してその形もわかっているとしたので\(y_0\)がわかった時に\(y_t\)のあたりがある程度つけられた.
ガウス過程は上記に「多変量ガウス分布を求める」が加わったに過ぎない. | 上記の流れとガウス過程 |
1.2.多変量ガウス分布の分散共分散を求める | |
上記のように多変量ガウス分布がわかっていれば、幾らかデータが得られると他の座標での値も推定できることがわかった. 今回は1つのデータと1つの予測のみ行う例だったが、実際は複数のデータと複数の予測でも同じことが行える.
ではどうやって多変量ガウス分布を求めるかということが気になる.
上記を考えるに当たり、ここではまず多変量ガウス分布がどういう分布であるべきかから考えていく.
多変量ガウス分布がどういう形になるとどういう関係になるかについて下記でまとめた. | 分散共分散行列を求める |
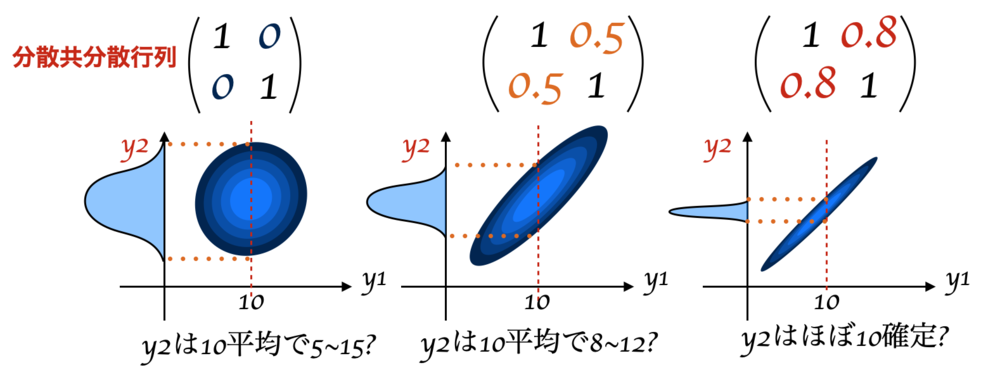 | 分散共分散行列がもとまると、片方が求まった時にもう片方がどう求まるかが決まる |
この図からわかるように、\(y1\)の値が分かっていても多変量ガウス分布の分散共分散行列が変わるとどんな\(y2\)になるかが変わってくる.
共分散の値が大きくなるにつれてどんどん分布は絞られた形になり、直線へと近づきほぼ比例したような関係になる. \(y1,y2\)の共分散の値が高くなると\(y1,y2\)はお互いに強く関係した値になっていく.
これをガウス過程の回帰でも生かす.
あるx座標\(x_1,x_2\)が非常に近いと、恐らく\(y_1,y_2\)は非常に近い値になり、\(y_1\)と\(y_2\)は比例するような関係になる.一方で、あるx座標\(x_1,x_100\)が非常に離れると、恐らく\(y_1,y_100\)は全く関係なく決まる.
つまり、\(x_1,x_2\)が近い時は\(y_1,y_2\)の共分散を高くなるようにし、\(x1,x_100\)が離れていれば\(y_1, y_100\)の共分散が0に近くなるようにすればよさそうだ
ガウス過程ではその共分散の値を計算する関数をカーネル関数\(k(x_0, x_1)\)として用意する. カーネル関数は特定の条件を満たしている関数であればなんでもよい. よく使われるカーネル関数はガウスカーネル/RBFカーネルと呼ばれる関数であり、以下のような関数.
$$k(x_0, x_1) = exp(-\frac{\Vert x_0 - x_1 \Vert ^2 }{2 \sigma^2 })$$
このカーネル関数の\(x0,x1\)に近い値を入れると1になり、かけ離れていると0になる. | ガウス過程で分散共分散を生かすには |
1.3.ガウス過程と多変量ガウス分布のまとめ | |
上記のようにして、
「分散共分散行列をカーネル関数で求めてデータから未知のデータを求める」
ことがガウス過程で行われる処理の流れです.
イメージはつかめたでしょうか?
次のところでは、数式でガウス過程の処理を追います.
| イメージのまとめ |
2.ガウス過程の簡易的な導出 | |
ここでは、こと細やかな導出は行わないものとします. 詳細な導出は他サイトでご確認ください. | 導出に当たって |
必要なときは右のリンクでベイズの公式等をご確認ください. | 外部リンク ベイズの公式等まとめ (ThothChildrenVisalgo) |
\(\boldsymbol{X_D}\)を複数のデータ\(N\)個の\(x\)座標、\(\boldsymbol{X_P}\)を複数\(M\)個の推定したい\(x\)座標とする.(またそれぞれy座標は\(Y_D, Y_P \))これらは両方ともある多変量ガウス分布から得られたはずで,
$$\begin{eqnarray}
P(\boldsymbol{Y})=
\left(
\begin{array}{c}
Y_D \\
Y_P
\end{array}
\right)
\sim N (
\left(
\begin{array}{c}
\boldsymbol{\mu_D} \\
\boldsymbol{\mu_P}
\end{array}
\right) ,
\left(
\begin{array}{c|c}
K_{X_DX_D} & K_{X_DX_P} \\
\hline
K_{X_PX_D} & K_{X_PX_P }
\end{array}
\right)
)
\end{eqnarray}$$
と書ける. \(K\)は各要素をカーネル関数で計算した値.例えば\(K_{XY}\)なら
$$
\begin{eqnarray}
K_{XY} =
\left(
\begin{array}{cccc}
k(x_{1},y_{1} ) & k(x_{2},y_{1} ) & \ldots & k(x_{n},y_{1} ) \\
k(x_{1},y_{2} ) & k(x_{2},y_{2} ) & \ldots & k(x_{n},y_{2} ) \\
\vdots & \vdots & \ddots & \vdots \\
k(x_{ 1},y_{m} ) & k(x_{2},y_{m} ) & \ldots & k(x_{n},y_{m} )
\end{array}
\right)
\end{eqnarray}
$$
と計算するものとする.
ここで一般的に
$$\begin{eqnarray}
\left(
\begin{array}{c}
A \\
B
\end{array}
\right)
\sim N (
\left(
\begin{array}{c}
\boldsymbol{\mu_A} \\
\boldsymbol{\mu_B}
\end{array}
\right) ,
\left(
\begin{array}{c|c}
K_{AA} & K_{AB} \\
\hline
K_{BA} & K_{BB}
\end{array}
\right)
)
\end{eqnarray}$$
であるなら
$$\begin{eqnarray}
P(B|A)
\sim N (
\mu_B + K_{BA}^T K_{AA}^{-1}(\boldsymbol{a} -\boldsymbol{\mu_A}) ,
K_{BB} - K_{BA}^TK_{AA}^{-1}K_{AB}
)
\end{eqnarray}$$
が成立する.
これは先の例でいうところの\(y0\)が分かっているときの\(y_t\)を求める計算と同じ.
$$\begin{eqnarray}
P(Y_P|Y_D)
\sim N (
\mu_P + K_{PD}^T K_{DD}^{-1}(Y_D -\mu_D ) ,
K_{X_PX_P} - K_{X_PX_D}^TK_{X_DX_D}^{-1}K_{X_DX_P}
)
\end{eqnarray}$$
以上の流れで、\(Y_D\)の値を使って\(Y_P\)の分布を求めることができた.
一般的に\(\mu_D\)や\(\mu_P\)は事前に分からず、0と仮定することが多い.
そうすると以下のようになる.
$$\begin{eqnarray}
P(Y_P|Y_D)
\sim N (
K_{PD}^T K_{DD}^{-1}Y_D ,
K_{X_PX_P} - K_{X_PX_D}^TK_{X_DX_D}^{-1}K_{X_DX_P}
)
\end{eqnarray}$$
| 簡易的なガウス過程の導出 |
上記で求められた、平均と分散の式で全ての点での平均と分散を求めることが可能になった.
実際にプログラムを書く場合は、求めたい\(x\)座標の値とデータを元に\(K\)の行列を計算すればよい. | ガウス過程の計算 |
この章を学んで新たに学べる
Comments


