-
 @ThothChildren
@ThothChildren
- 2018.10.23
- PV 543
ヒルベルト曲線
ー 概要 ー
ヒルベルト曲線(Hilbert Curve)は、平面や空間内の単位正方形、単位立方体を特定のパターンに乗っ取って全て通るフラクタルな空間補充曲線の一つ.(一本の線で全部のブロックを通るようにする)他の空間充填曲線によってマッピングを行うよりもより位置関係を保持する曲線になっている.応用例も多く、空間インデックスや検索、などがある.1次元の値がn次元に対応しているため、原点からの距離が近いとその空間でも近いとわかる.
この章を学ぶ前に必要な知識
効果
- 1次元の値域と高次元の空間を割り当てる
- 空間や平面の単位正方形、単位立方体を全て通る曲線を描ける
- 他の空間充填曲線より位置関係を保持できる
ポイント
- 1次元の距離が近いなら、対応する平面または立体でも近い
- 対応する平面または立体で近い点でも、1次元の距離が近いとは限らない
解 説
ヒルベルト曲線(Hilbert Curve)は、平面や空間内の単位正方形、単位立方体を特定のパターンに乗っ取って全て通るフラクタルな空間補充曲線の一つ.
他のマッピングを行うよりもより局所性が高い曲線になっている.応用例も多く、地理情報などをデータ化する空間インデックスやヒルベルトR-Treeなどに用いられる.
特徴
・1次元上の距離が近いとその空間でも近いとわかる.
・しかし、逆に空間上で近くても1次元上の距離が近いとは限らない
・フラクタルな図形になっており、ヒルベルト曲線からより細かいヒルベルト曲線を再帰的に作成できる
・ヒルベルト曲線の距離は、n回のフラクタル処理で(n次で)2^n-1/2^n | ヒルベルト曲線とは |
 | ヒルベルト曲線の成長の様子.
フラクタル図形であるため、左のような形で細かくしていくことができる.
(https://upload.wikimedia.org/wikipedia/commons/4/46/Hilbert_curve.gif より引用) |
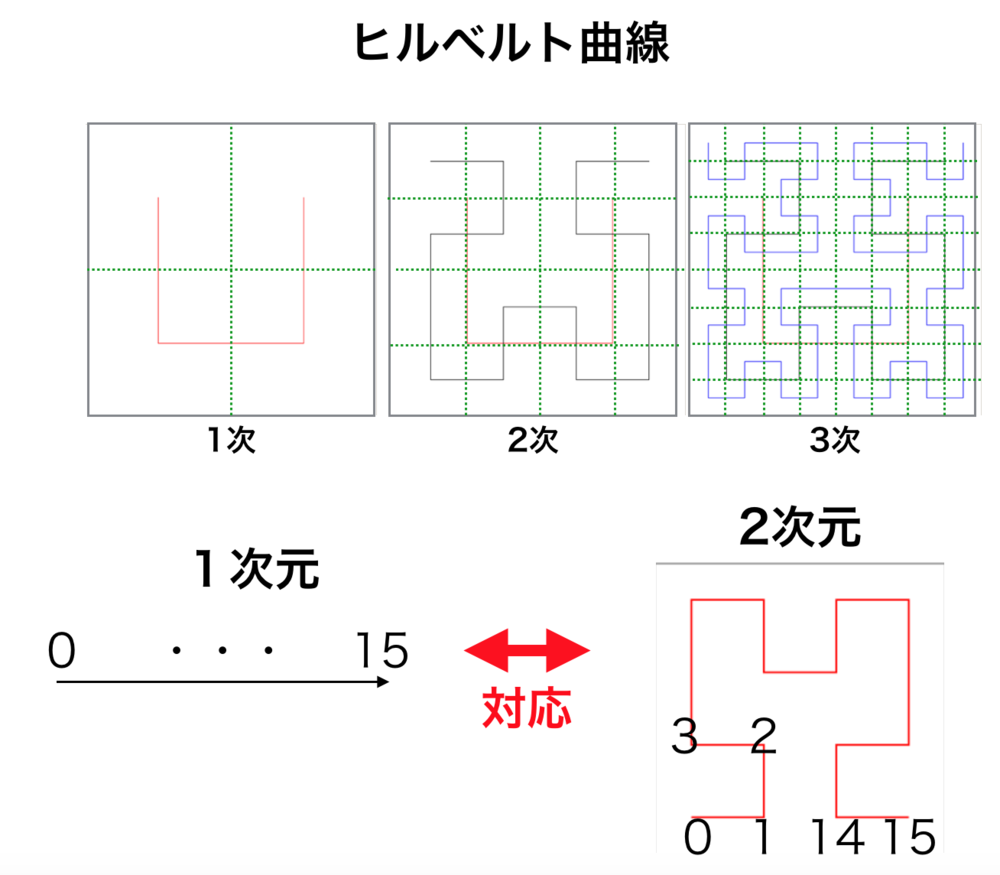
 | ヒルベルト曲線の1次元と2次元の対応例 |
この章を学んで新たに学べる
Comments


