-
 @ThothChildren
@ThothChildren
- 2018.10.24
- PV 372
ペアノ曲線
ー 概要 ー
ペアノ曲線(Peano Curve)は、一次元の値域を単位正方形(n次元でも可)に往復する形で対応させて実現したフラクタルな空間充填曲線.空間充填曲線を一般的に指す時もある.

この章を学ぶ前に必要な知識
効果
- 一次元の値域をn次元に対応させる
ポイント
- ペアノ曲線はフラクタルな空間充填曲線
- ヒルベルト曲線が持つ特徴を多く持つ
- 最小が3x3のマスを通るペアノ曲線
- ヒルベルト曲線にはない回文性質を持ち、子の9マスは隣接するマスと必ず反転
- 3x3がベースとなってしまうため、2進数のような扱いを行いビット演算ができないのが欠点
- 次数の異なるマスを結ぶ時に3x3の大きさが扱いにくい
解 説
ペアノ曲線(Peano Curve)は、一次元の値域を単位正方形(n次元でも可)に往復する形で対応させて実現したフラクタルな空間充填曲線.空間充填曲線を一般的に指す時もある.
ペアノ曲線特徴
・ペアノ曲線はフラクタルな空間充填曲線.1次、2次、とより細かくなっていく.自己相似性を持つ.
・1次のペアノ曲線は3x3のマスを通る曲線
・ヒルベルト曲線が持つ特性を多く持っているが、ヒルベルト曲線にはない回文性質を持ち、子の9マスは隣接する子マスと必ず反転した形状となっている.(どの方向にも)
・1次のペアノ曲線は3x3がベースとなってしまうため、ヒルベルト曲線のように2進数のような扱いを行いビット演算ができないのが欠点
・異なった次数のマスを結びつけるAdaptive Refinementのときは、ペアノ曲線は荒くなりがち
| ペアノ曲線 |
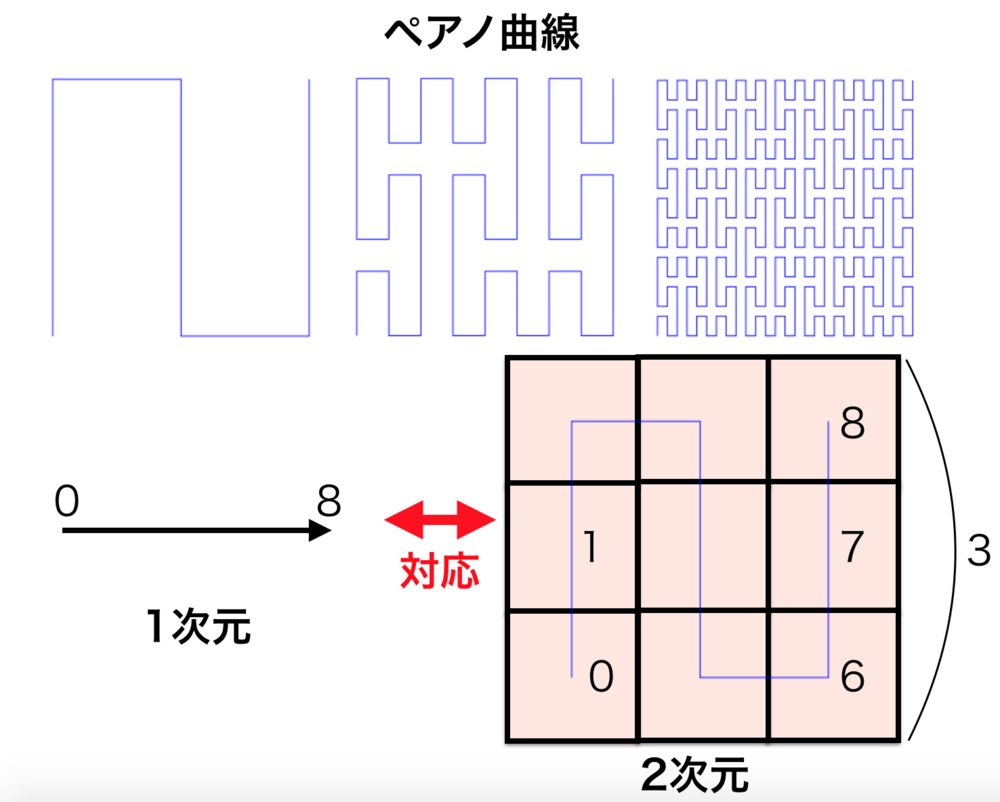 | ペアノ曲線の図.
上側は1次ペアノ曲線、二次、三次
下側は1次元と二次元を対応させている様子 |
この章を学んで新たに学べる
Comments


