©2024 Thoth Children All rights reserved.

グラフの最短路探索

データをグラフ形状で表現できている時に、それらの経路にはコストが決められており、もっともコストが少なくなるように与えられた始点と終点の間の経路を探索するアルゴリズムについてまとめます.ベルマンフォードやダイクストラ法によるものなどが代表的な方法です.
2018.7.22
  • 52
    Views
  • 0
    Watch
  • 4
    Knows

グラフの最短路探索の新規投稿

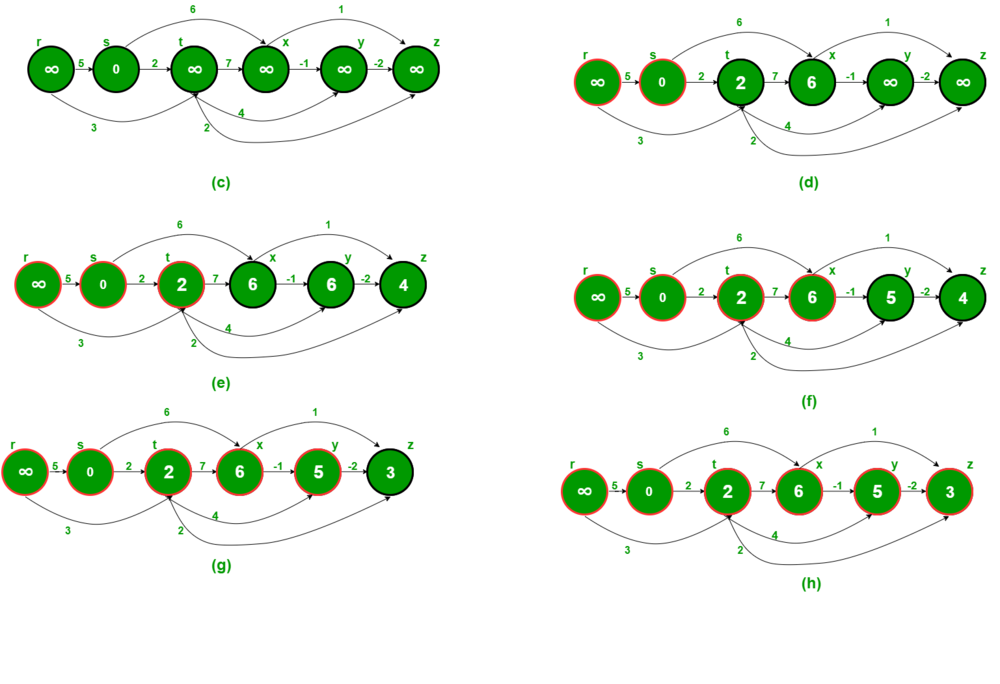
トポロジカルソートのDAG経路探索
有向非循環グラフ(DAG)の最短経路探索を線形時間で探索を行う手法として、トポロジカルソートによるものが挙げられます.一度しかノードもエッジも参照しないため、ソート自体もその後の最短経路探索も線形時間で探索が完了します.
PV 215
Fav 0
2018.10.21
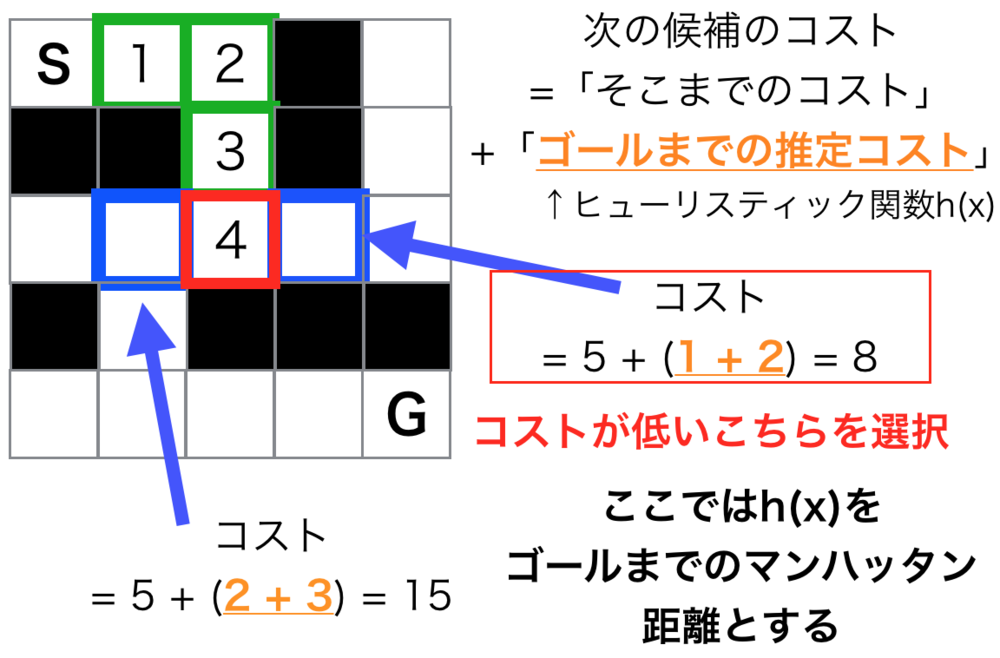
A*探索アルゴリズム
A*探索アルゴリズムは候補のノードのうち「それまでのコスト」+「ゴールまでの推定コスト」が最小になると思われるノードを繰り返し選択していき効率的に最短経路を探索するアルゴリズム.ダイクストラの一般化であり、「ゴールまでの推定コスト」を0にしているのがダイクストラ法.「ゴールまでの推定コスト」は自身で決める必要があり、その質に探索の効率が大きく左右される.
PV 385
Fav 0
2018.08.08
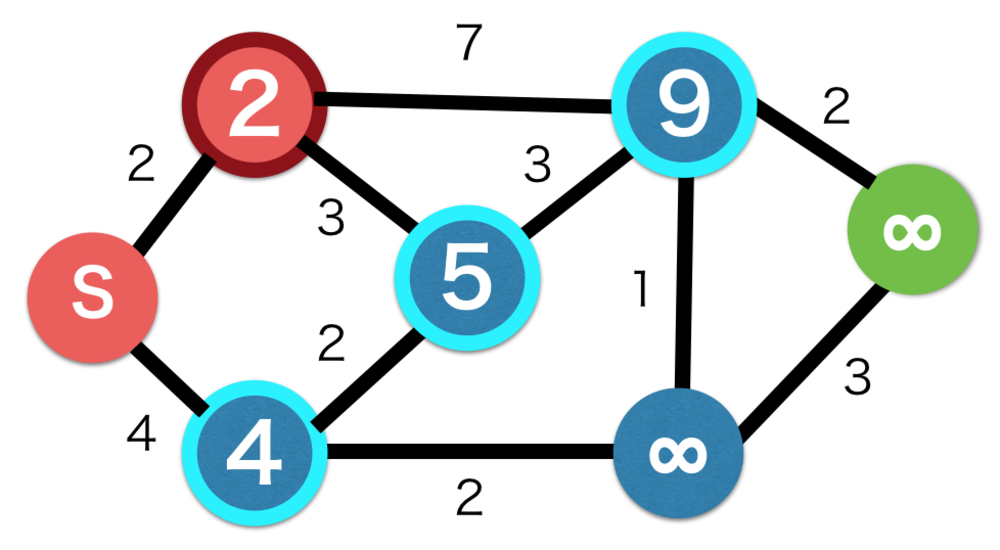
ダイクストラ法
ダイクストラ法は、負のコストがない回路において、ルートを選択を工夫して最短経路を見つけ出していくことで、ベルマンフォード法より効率的に探索することのできるアルゴリズム.普通の実装では計算量はO(n^2)だが、適当なヒープを用いることでO(E+nlog(n))になる.
PV 294
Fav 0
2018.08.08
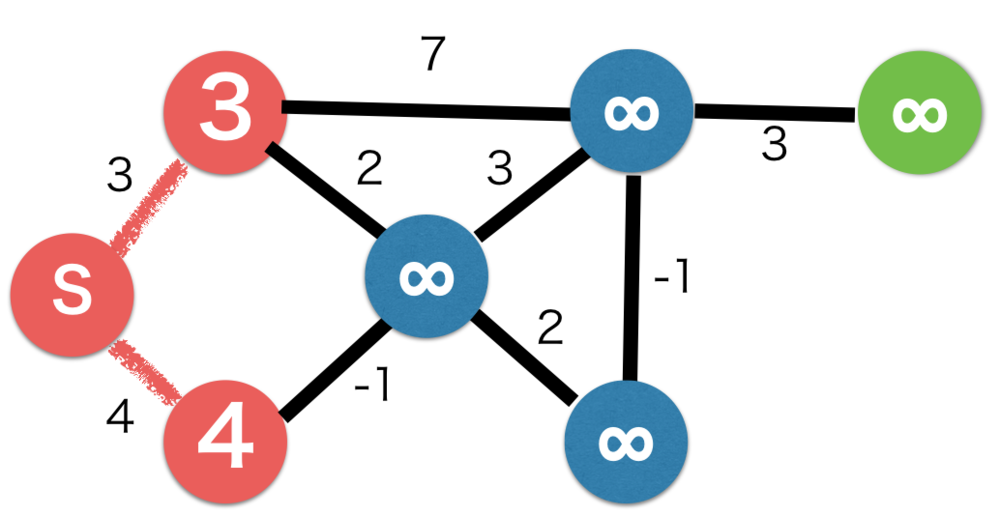
ベルマンフォード法
ベルマンフォード法は、コストがついた辺をもつグラフにおいてある始点からある終点までの最短コストの経路を探索するアルゴリズムです.ベルマンフォードはダイクストラと異なり負の値も扱うことができます.もし一周したコストが負になる箇所があるとそこをぐるぐる回り続けることによっていくらでもコストを避けられるため、そのようなグラフでは解を持ちません.
PV 540
Fav 0
2018.07.24

グラフの最短路探索人気知識・質問

ベルマンフォード法
ベルマンフォード法は、コストがついた辺をもつグラフにおいてある始点からある終点までの最短コストの経路を探索するアルゴリズムです.ベルマンフォードはダイクストラと異なり負の値も扱うことができます.もし一周したコストが負になる箇所があるとそこをぐるぐる回り続けることによっていくらでもコストを避けられるため、そのようなグラフでは解を持ちません.
PV 540
Fav 0
2018.07.24
A*探索アルゴリズム
A*探索アルゴリズムは候補のノードのうち「それまでのコスト」+「ゴールまでの推定コスト」が最小になると思われるノードを繰り返し選択していき効率的に最短経路を探索するアルゴリズム.ダイクストラの一般化であり、「ゴールまでの推定コスト」を0にしているのがダイクストラ法.「ゴールまでの推定コスト」は自身で決める必要があり、その質に探索の効率が大きく左右される.
PV 385
Fav 0
2018.08.08
ダイクストラ法
ダイクストラ法は、負のコストがない回路において、ルートを選択を工夫して最短経路を見つけ出していくことで、ベルマンフォード法より効率的に探索することのできるアルゴリズム.普通の実装では計算量はO(n^2)だが、適当なヒープを用いることでO(E+nlog(n))になる.
PV 294
Fav 0
2018.08.08
トポロジカルソートのDAG経路探索
有向非循環グラフ(DAG)の最短経路探索を線形時間で探索を行う手法として、トポロジカルソートによるものが挙げられます.一度しかノードもエッジも参照しないため、ソート自体もその後の最短経路探索も線形時間で探索が完了します.
PV 215
Fav 0
2018.10.21