-
 @ThothChildren
@ThothChildren
- 2018.7.24
- PV 598
ベルマンフォード法
ー 概要 ー
ベルマンフォード法は、コストがついた辺をもつグラフにおいてある始点からある終点までの最短コストの経路を探索するアルゴリズムです.ベルマンフォードはダイクストラと異なり負の値も扱うことができます.もし一周したコストが負になる箇所があるとそこをぐるぐる回り続けることによっていくらでもコストを避けられるため、そのようなグラフでは解を持ちません.
この章を学ぶ前に必要な知識
条件
- コストを辺に持つグラフ
- コストは負でも構わない
効果
- ある始点からある終点までの最小コストの経路を得る
ポイント
- 最悪時間計算量はO(VE)
- 初めは始点以外の頂点に到達するコストを全て無限にし、更新していく
- コストの更新が起こらなければ終了
解 説
ベルマンフォード法は、コストがついた辺をもつグラフにおいてある始点からある終点までの最短コストの経路を探索するアルゴリズムです.
ベルマンフォードはダイクストラと異なり負の値も扱えます.もし一周したコストが負になる箇所があるとそこをぐるぐる回り続けることによっていくらでもコストを避けられるため、そのようなグラフでは解を持ちません. | ベルマンフォード法について |
コストに負の値がない限り、ダイクストラの法が高速なのでベルマンフォード法は使用しません.
また、ベルマンフォード法によって負の閉路を検出することができます. | ベルマンフォード法の補足 |
ベルマンフォード法によるアルゴリズム
1. すべての頂点のコストを「無限」に設定する.スタート地点だけコストが0.
2. 辺UVに注目して「頂点Uのコスト」+「辺のコスト」<「頂点Vのコスト」なら頂点Vのコストを「頂点Uのコスト」+「辺のコスト」で更新
3. どのノードで更新したかを記録しておく
4. 2~3を全ての辺に対して行う.
5. 2~4を(頂点の数-1)回行う か コストの更新が止まれば終了.
「5」で頂点数V-1回更新するのと、1度の更新で全ての辺E個を更新するため、時間計算量はO(VE)となります. | ベルマンフォード法によるアルゴリズム |
1.ベルマンフォードの例 | |
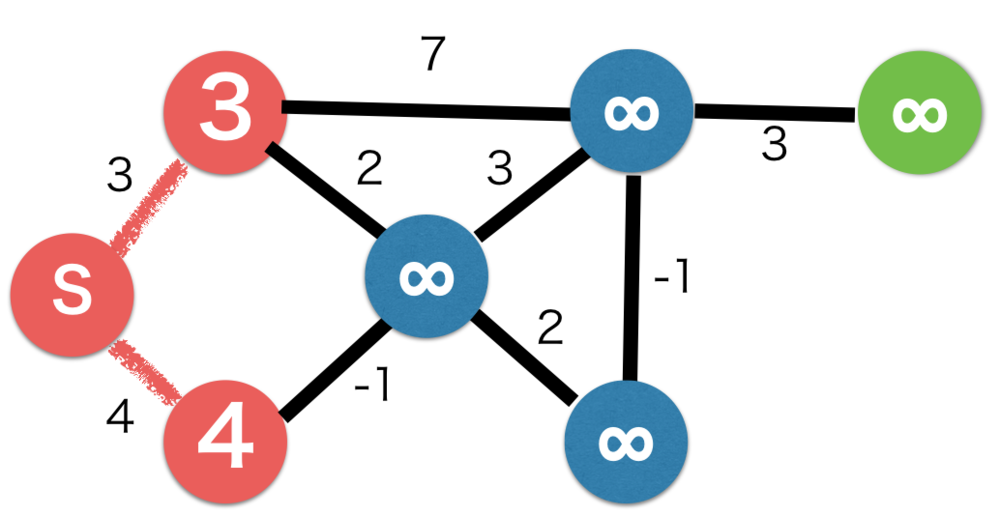
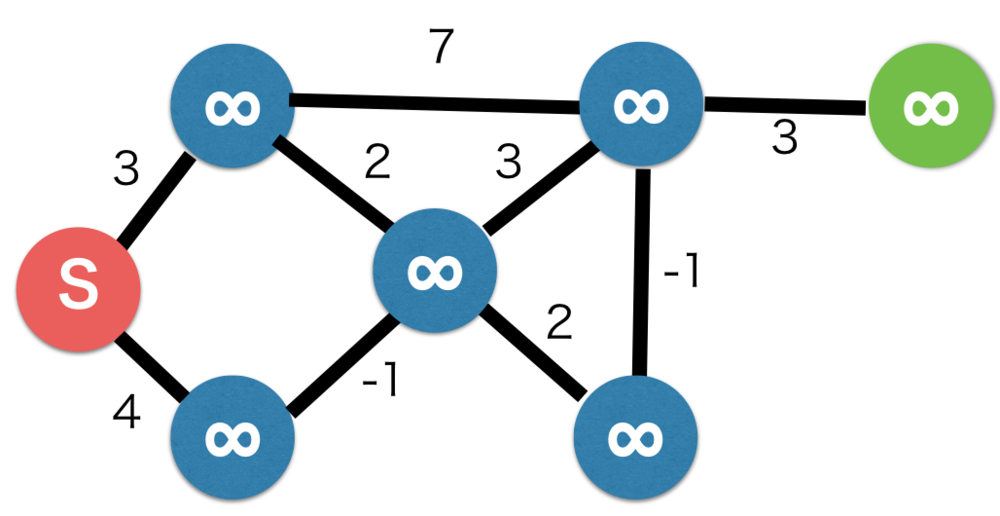 | 全てのコストを初期化します.
全て無限に設定しています. |
 | 左図は一回目の全辺更新の途中です.
スタートから少しずつ更新をしていきます.
3と4が最短距離となっています. |
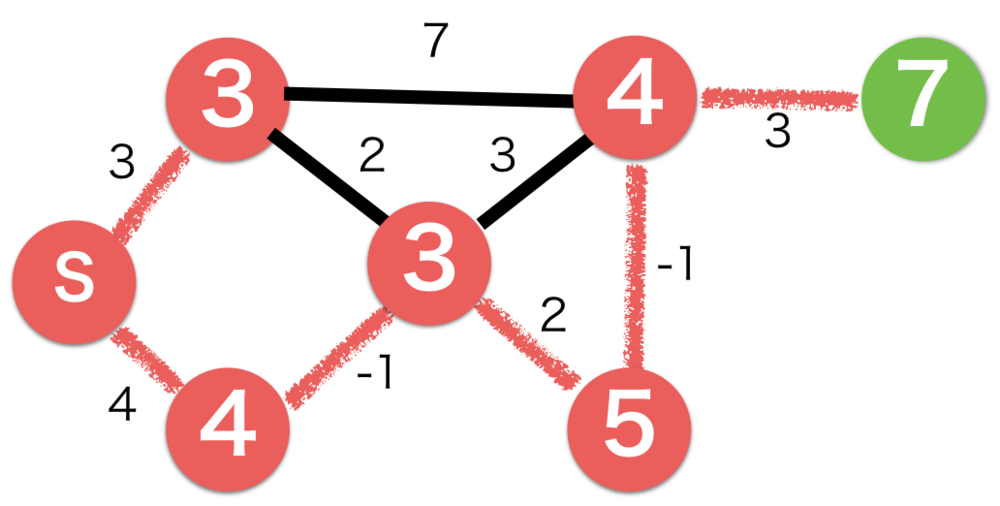 | 上のように更新をしていき
一回目の更新を終えました.
今回はもう一度全ての辺を更新してもコストの更新はありません.
そのため更新は以上で終わりになります.
最短経路とコストが7であることがわかりました. |
この章を学んで新たに学べる
Comments


