A*探索アルゴリズム

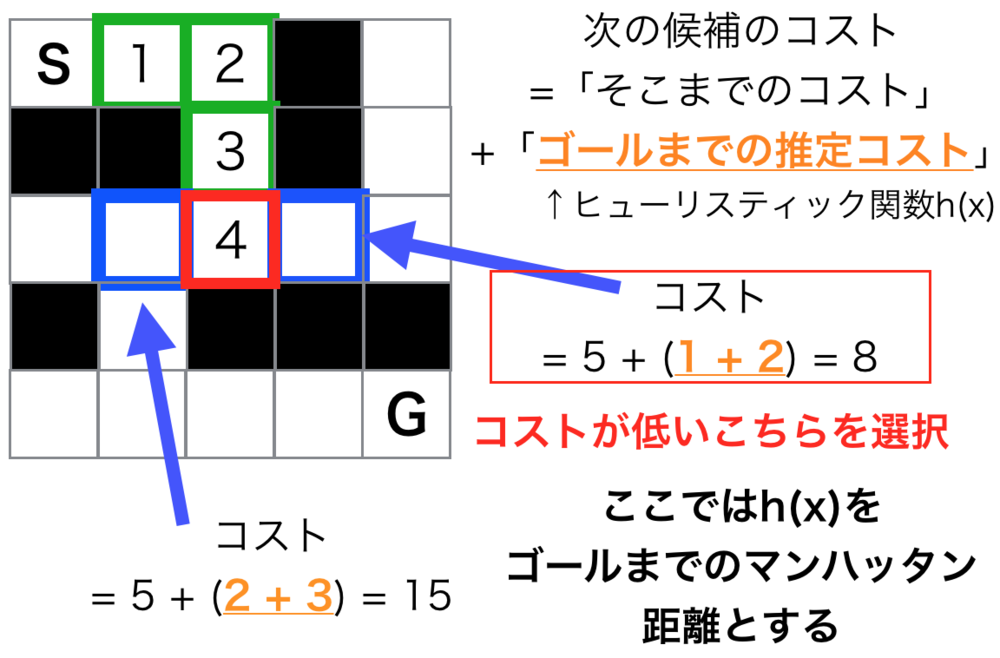
A*探索アルゴリズムは候補のノードのうち「それまでのコスト」+「ゴールまでの推定コスト」が最小になると思われるノードを繰り返し選択していき効率的に最短経路を探索するアルゴリズム. ダイクストラの一般化であり、「ゴールまでの推定コスト」を0にしているのがダイクストラ法. 「ゴールまでの推定コスト」は自身で決める必要があり、その質に探索の効率が大きく左右される.これをヒューリスティック関数h(x)と呼ぶ.例えば二次元のグラフ上ではゴールまでのユークリッド距離やマンハッタン距離などを用いると大方筋の良い評価関数となる. 常に最小のコストを見つけ出すことができる.

A*はよく以下のように表記される. $$f(n) = g(n) + h(n)$$ このとき\(f(n)\)はノードの推定コスト、\(g(n)\)はスタートノードからそのノードまでの最小コスト、\(h(n)\)はそのノードからゴールのどまでの推定コストを表す.

A*探索アルゴリズム処理のながれ概要 1. 候補となるノードを入れたOpenリストと計算を終えているCloseリストを用意 2. スタートノードをOpenリストに加える. 3. 「Openリストが空」か「Openリストの最小コストのノードにゴールがある」なら終了. 4. 最小コストのノードを取り出して、その隣接するノードを先のコスト計算式で更新. 5.3からを終わるまで繰り返す.