-
 @ThothChildren
@ThothChildren
- 2019.3.3
- PV 1201
セカント法による求根
ー 概要 ー
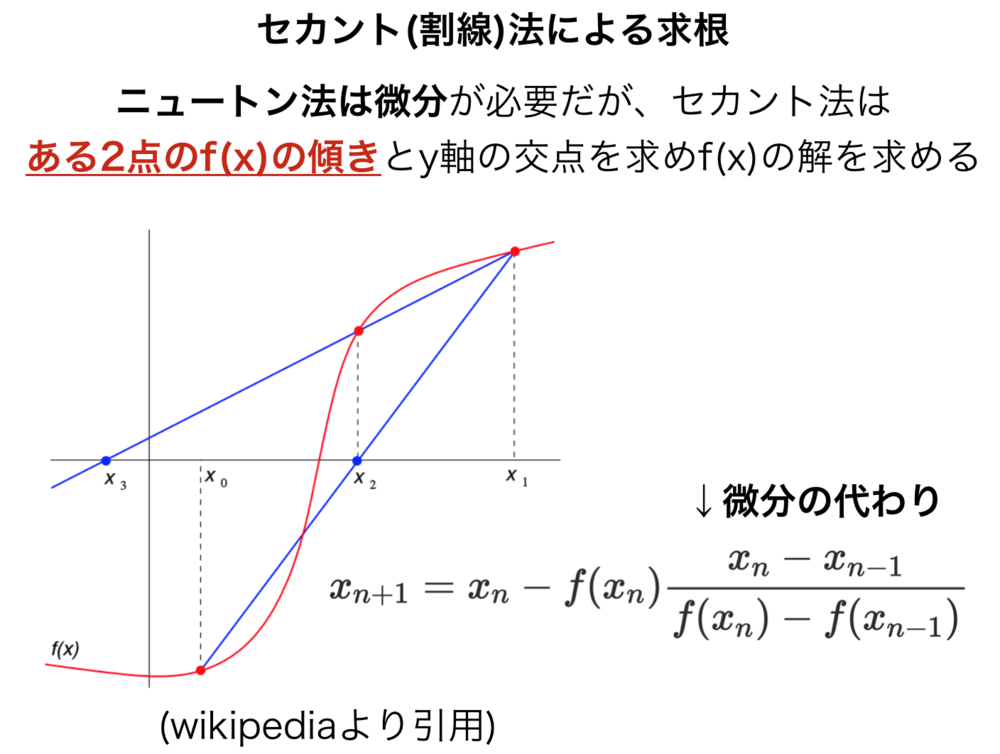
セカント法(割線法)は、関数が0になる変数の値を求めることができる球根アルゴリズムで、ニュートン法では微分できることが必要でしたが、その必要はなく一つ前の解との差分から傾きを計算する手法です.ここでは一次元のみ紹介します.セカント法はニュートン法と異なり二次収束しないため、ニュートン法ほどの収束の速さは保証されませんが関数によっては早くなります.
この章を学ぶ前に必要な知識
条件
- 関数と二つの初期値が必要
効果
- f(x)=0となるような解を求めることができる
ポイント
- ニュートン法のような二次収束は保証されないため、大方ニュートン法より遅い
- 微分が困難な関数で適用可能
- ここでは1次元の場合を紹介
- ニュートン法の微分を二点の傾きに置き換えただけ
解 説
この章を学んで新たに学べる
Comments
Reasons
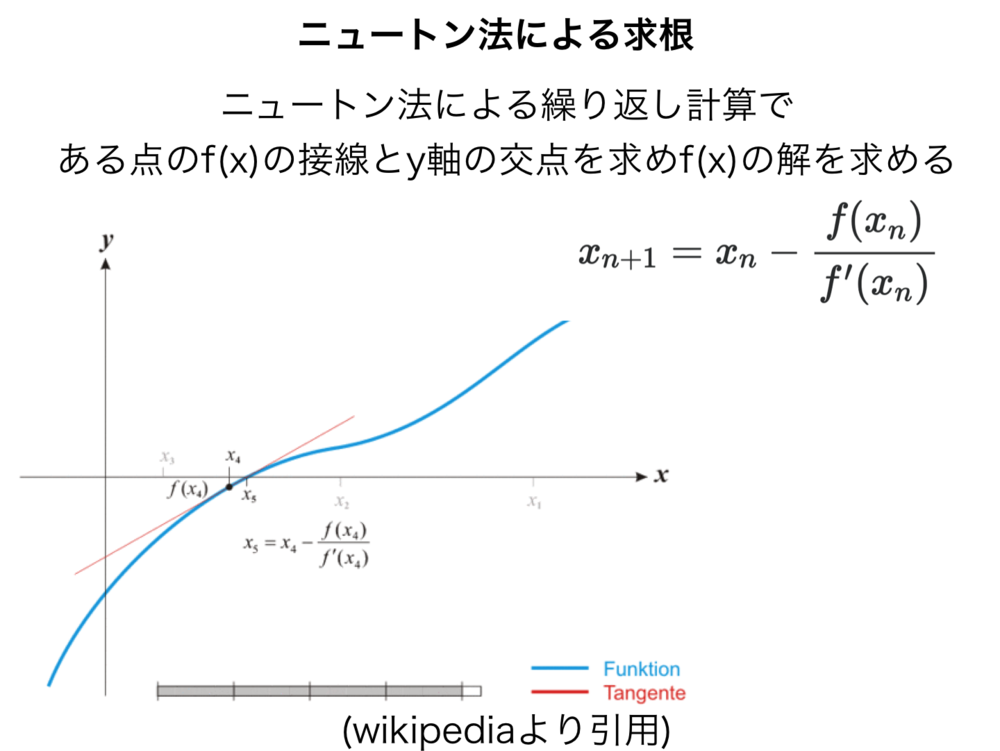
知識: ニュートン法による求根
求根アルゴリズムとして有名である頻繁に使用されるニュートン法(1次元の場合)について紹介します.ニュートン法によって関数の値がゼロになる値等を算出します.探索する初期値に依存し、解は一つしか見つけられませんが、比較的高速です.導関数が適切に得られる必要があります.


