-
 @ThothChildren
@ThothChildren
- 2019.3.2
- PV 940
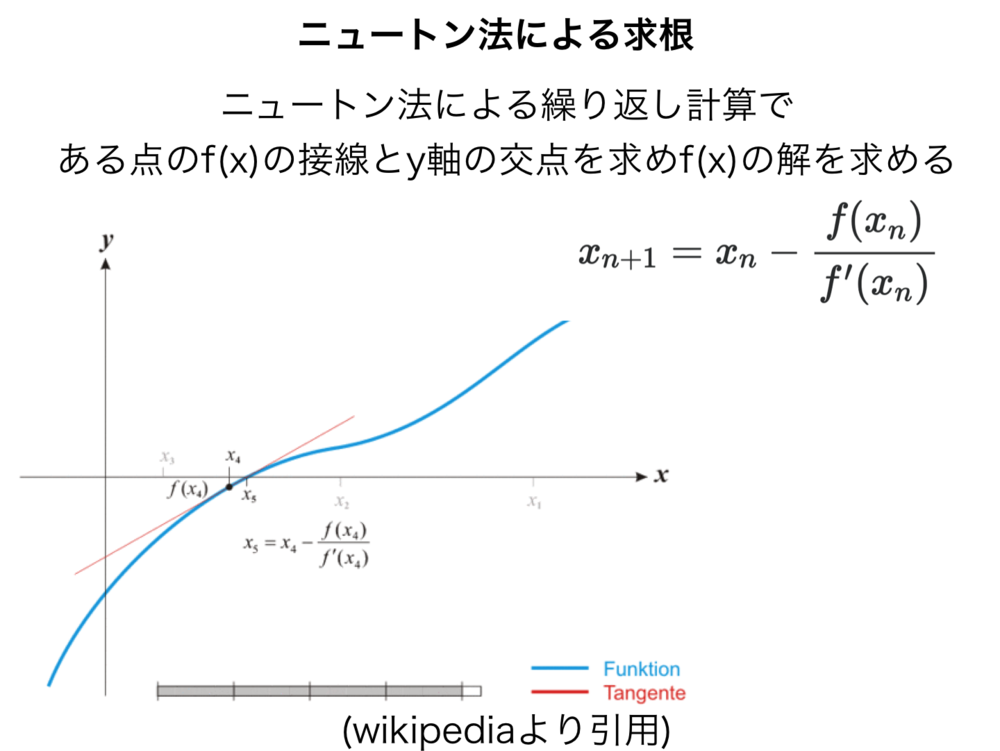
ニュートン法による求根
ー 概要 ー
求根アルゴリズムとして有名である頻繁に使用されるニュートン法(1次元の場合)について紹介します.ニュートン法によって関数の値がゼロになる値等を算出します.探索する初期値に依存し、解は一つしか見つけられませんが、比較的高速です.導関数が適切に得られる必要があります.
この章を学ぶ前に必要な知識
条件
- 関数の導関数が求められること
- 探索開始の初期値が解に近いこと(遠すぎると収束しない)
効果
- 導関数が得られればどのような関数でも方程式の解が得られる
- 多次元にも適用可能
ポイント
- 得られる解は一つのみ.複数必要な場合は工夫が必要.
- f(x)=g(x)の解が求めたい場合は移項してf(x)-g(x)=0とすればよい
- 比較的高速だが初期値に強く依存
- 毎回その点での傾きから数値を傾いている方に点を動かしていく
- 二次収束となる
解 説
わかりやすいニュートン法による最適化の解説動画 | |
非線形な関数に適用できる求根アルゴリズムとして有名である頻繁に使用されるニュートン法について紹介します.ニュートン法によって関数の値がゼロになる値等を算出します(近似的に求めます).
求まる解が探索する初期値に依存しまた適切な初期値でないと収束しない(解がもとまらないこと)もあり得ます.他の球根アルゴリズムより比較的高速です
工夫がないと解は一つしか見つけられないため、何らかの方法で解を絞っていく方法が必要になります.
ニュートン法概要
反復法による解の更新によってf(x)=0になるxを求める.
毎回現在のx座標での傾きから数値を傾いている方にx座標を更新していく.
上記のように傾きを扱うため、導関数が関数から求められる必要があります. | ニュートン法による求根について |
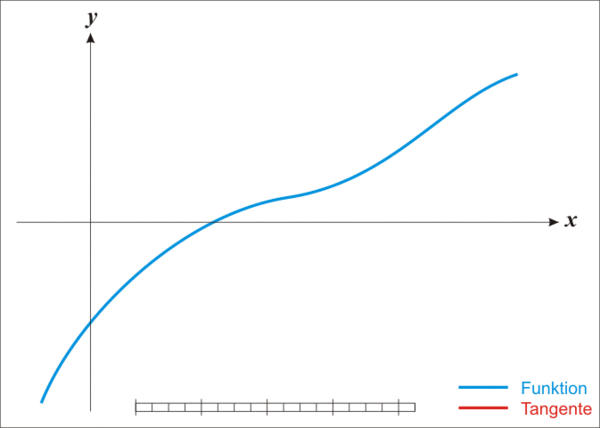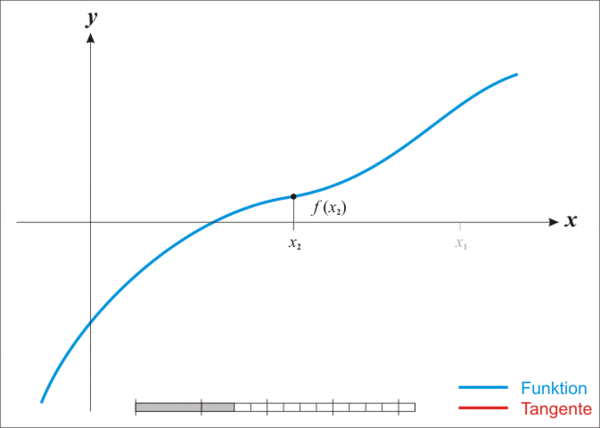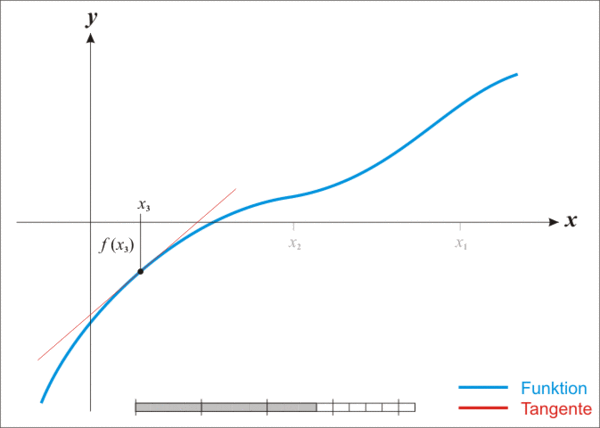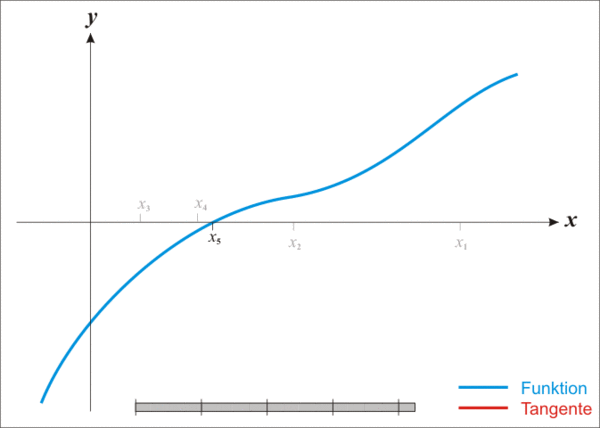 | Wikipediaより引用.
ニュートン法によって解が少しずつ近いづいていることがわかる. |
ニュートン法の更新式
解を求めるにあたり、以下の式に沿って反復計算を行う.
$$x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}$$
ニュートン法の手順
1. 適切な解に近い初期値\(x_0\)を決める.(遠すぎると収束しないため)
2. 上記の更新式と初期値\(x_0\)から次の\(x_1\)を求める.
3. \(x_1\)と更新式により新しい\(x_2\)といった作業を繰り返し行う.
4. 十分な精度になったら\(x_n\)を出力して処理を停止する.
この式の導出は非常に簡単である.
ニュートン法は、「解に近い点での接線」は「解となるx座標」と近いところで\(y=0\)と交わることを利用 して解を求める.
そのため、繰り返す計算は
接線を計算してy軸との交点を求めること
となる.
一般的に接線は\(x=\alpha\)での接線は以下で求められる.\(x=\alpha\)を代入すれば、\(y=f(\alpha)\)となることが確認できる.
$$y = f'(\alpha )(x - \alpha ) + f(\alpha) $$
この接線と\(y=0\)が\(x=\beta\)と交わったとすると上記の式に代入して
$$0 = f'(\alpha )(\beta - \alpha ) + f(\alpha)$$
となる.
\(\beta\)が次のx座標なのでこれを求める形に変形すると
$$\beta = \alpha - \frac{f(\alpha )}{f'(\alpha )}$$
と求められ、\(\beta\)が更新後の値、\(\alpha\)が更新前の値なので、これを漸化式のように書き換えるとはじめに示した式となる
$$x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}$$ | ニュートン法 |
ニュートン法は、解の区間で微分可能な非線形の関数に対して用いることができ、
また比較的高速な上に、高次元に対しても容易に適用できることから重宝される.
ただ、解は一つしかもとまらず、初期値に強く依存して解が決まるため、
複数の解を得るには何らかの工夫が必要となる. | ニュートン法の特徴 |
多項式の複数の解を求める方法として以下のような方法が考えられる.
多項式の複数解を全て求める
1. 多項式\(P(x)\)に対して初期値を与えてニュートン法により一つ解\(\alpha \)を求める.
2. (x-\(\alpha \))で多項式\(P(x)\)を割る. (解なので必ず割り切れる)
3. 割った後の多項式\(Q(x)\)を新しい\(P(x)\)として1.より始める.
4. 割った後の多項式\(Q(x)\)の次数が1になるまで繰り返す.
具体的には
0. 以下の式の解を全てニュートン法で求めるとする.
$$P(x)=f(x)= x^3 - 2x^2 -x + 2$$
1. 1度目のニュートン法で\(x = 2\)が決まったとする.
2. \((x-2)\)で多項式\(f(x)\)を割ることで
$$Q(x) = x^2 - 1$$
を得る.
3. 上記の\(Q(x)\)を新しい\(P(x)\)として次の解を求める.
ここで\(x = 1\)と新しい解が求まったとすると,
\(Q(x) = x + 1\) となる.
4. 上記の式の次数は1なので
$$f(x)=(x-1)(x+1)(x-2)$$
と解が\(x=1,-1,2\)であったことがわかる.
計算誤差がたまるため、精度高く解を求めないと他の解にも影響してくる. | 多項式の解をニュートン法で全て求めるには |
この章を学んで新たに学べる
Comments


