<<展開
©2022 Thoth Children All rights reserved.

逆数の計算を計算の置換えで早くする

ー 概要 ー

逆数の計算は愚直に実装をすると遅くなってしまいます.そこでニュートン法を用いることで逆数の計算を引き算と2回掛け算の反復処理に変換することで高速に求めます.
Facebookシェア Twitterツイート LINEで送る このエントリーをはてなブックマークに追加
この章を学ぶ前に必要な知識
0
効果
  • ニュートン法によって逆数の計算を引き算と掛け算2回の反復に置き換え
ポイント
  • 反復計算のため精度は反復回数に依存します
  • f(x) = a - 1/x = 0のxをニュートン法によって求めます

解 説

逆数の計算は愚直に実装をすると遅くなってしまいます.そこでニュートン法を用いることで逆数の計算を引き算と2回掛け算の反復処理に変換することで高速に求めます. 反復処理において何回計算するかで求まる逆数の値の精度が変わります.当然回数が多いほど精度は高まります.
逆数を計算の置換えで早くする
ニュートン法に関してはリンクを参照してください.
ニュートン法による求根
\(\alpha\)の逆数が求めたいとした場合、ニュートン法を以下の式に対して用いる. $$f(x) = \alpha - \frac{1}{x}$$ これが0となる点は、\(x = \frac{1}{\alpha}\)となるはずである. \(f(x)\)の微分は $$ f'(x) = \frac{1}{x^2 }$$ なので ニュートン法によって導かれる式は、 $$x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}\\ = x_n - \frac{\alpha - \frac{1}{x_n}}{\frac{1}{x_n^2}} \\ =x_n - \alpha x_n^2 +x_n \\ = 2x_n - \alpha x_n^2 \\ = x_n (2 - \alpha x_n) $$ と求まる. つまり、いかが更新式 $$x_{n+1} = x_n (2 - \alpha x_n) $$
ニュートン法による逆数計算の反復計算への置き換え
$$x_{n+1} = x_n (2 - \alpha x_n) $$ の計算を見ればわかるように この計算は一回の引き算と二回の掛け算によって求められる. これを必要な精度になるまで繰り返すことで逆数を求めることができる.
ニュートン法による逆数計算の補足説明
C++
?
1
2
3
4
5
double value = 7; //taget value
double update(double x_n){
    double x_n1 = x_n * ( 2 - value * x_n );
    return x_n1;
}
逆数を求めたい対象をvalueとしています. update関数においては更新式に基づいてより良い値を求めています.
この章を学んで新たに学べる
Comments

Reasons
>>隠す

知識: ニュートン法による求根
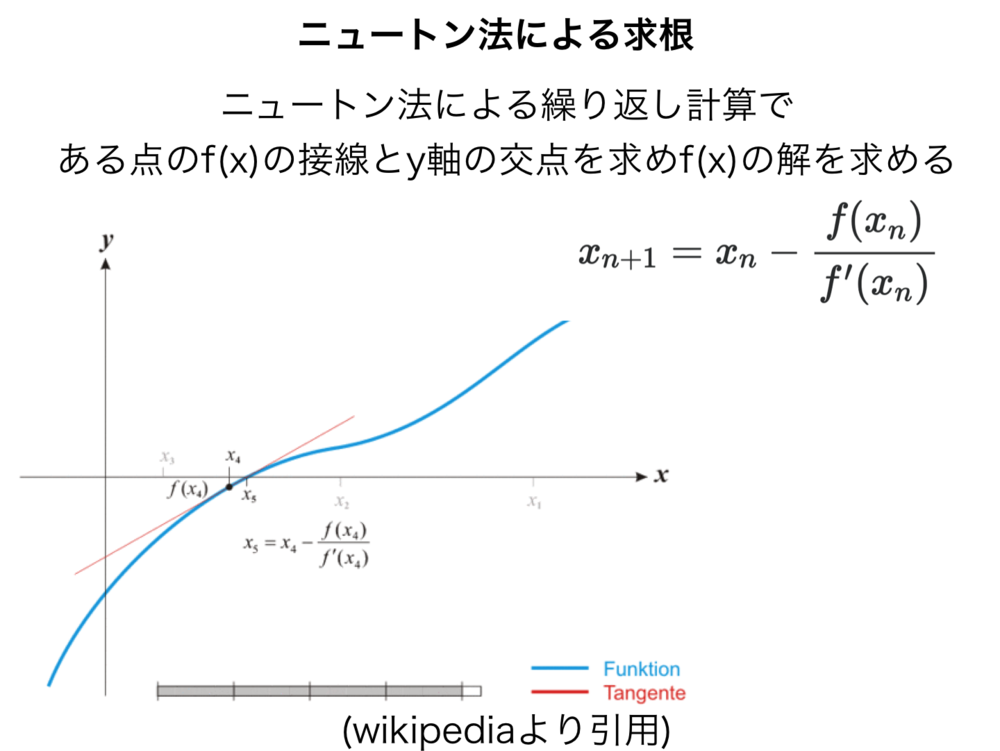
求根アルゴリズムとして有名である頻繁に使用されるニュートン法(1次元の場合)について紹介します.ニュートン法によって関数の値がゼロになる値等を算出します.探索する初期値に依存し、解は一つしか見つけられませんが、比較的高速です.導関数が適切に得られる必要があります.