<<展開
©2024 Thoth Children All rights reserved.

DoG

ー 概要 ー

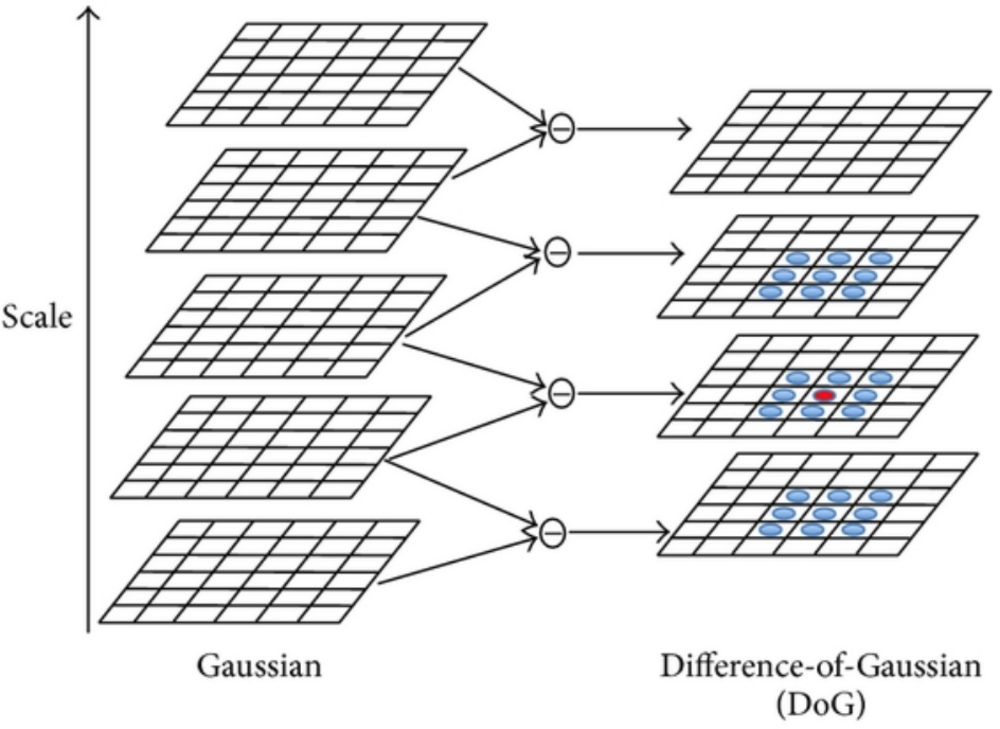
DoG(Difference of two Gaussian)は、LoGでの重いフィルタ処理をガウシアンの差分によって近似し軽量化したフィルタ.各スケールσ、kσ、k^2σ、等σの大きさを変えてフィルタ処理したのちにその差分を計算.値が０になっているところがエッジ. 上記のような工夫をしても尚、σを大きくしたガウシアンフィルタの計算は重いため、σを大きくするのではなく、入力画像をダウンサンプリングすることでさらなる軽量化を行います
Facebookシェア Twitterツイート LINEで送る このエントリーをはてなブックマークに追加
この章を学ぶ前に必要な知識
0
条件
  • 画像が入力
効果
  • 軽量化したLoGの近似した結果が得られる
ポイント
  • LoGの計算が重たいためDoGの形で近似を行う
  • DoGでは二つのスケール値(σ)を使ってガウシアンフィルタを計算し、その結果の差分を得る
  • またσが大きくするとガウシアンフィルタの処理が重いため、σ大きくせずに入力画像を小さくして差分を得る
  • 上記のように二つの近似を行って高速に計算

解 説

DoG(Difference of two Gaussian)は、LoGでの重いフィルタ処理をガウシアンの差分によって近似し軽量化したフィルタ. 各スケールσ、kσ、k^2σ、等σの大きさを変えてガウシアンフィルタ処理したのちにそれらの差分を計算(工夫1).LoGと同様に値が０になっているところがエッジとして検出される. 上記のような工夫をしても尚、σを大きくしたガウシアンフィルタの計算は重いため、いつまでもσを大きくするのではなく、あるタイミングで入力画像をダウンサンプリングする(工夫2)ことでさらなる軽量化を行います.これはあくまで近似です.
DoGとは
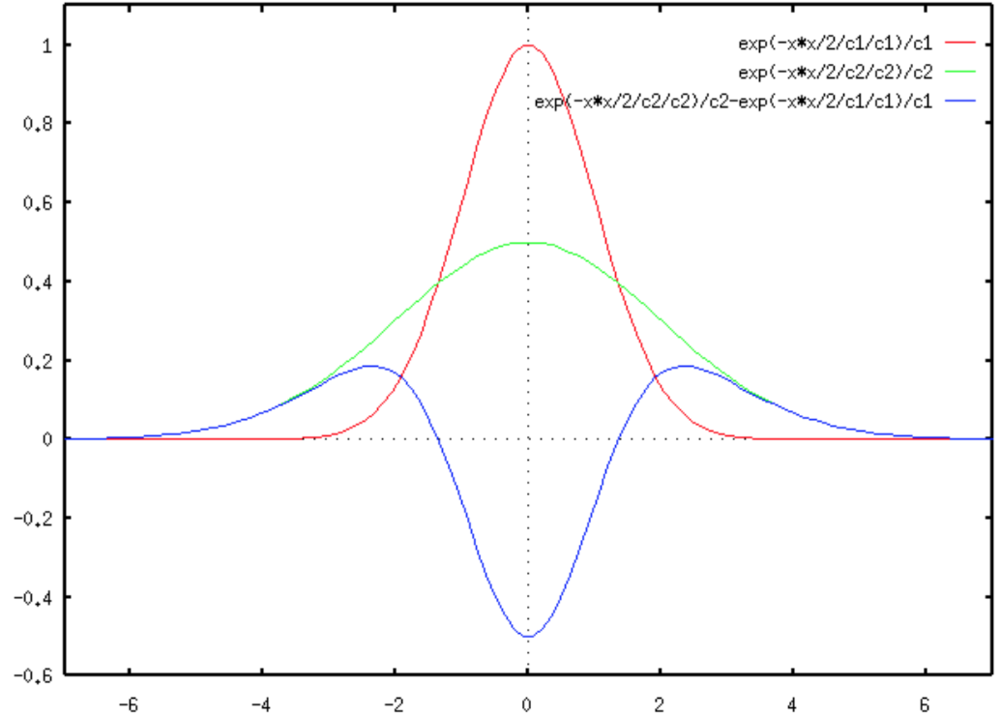赤と緑の線は、ある大きさσのガウシアン分布. それらの差分を青で示している. この形状はLoGで得られる図形と非常に似ている.
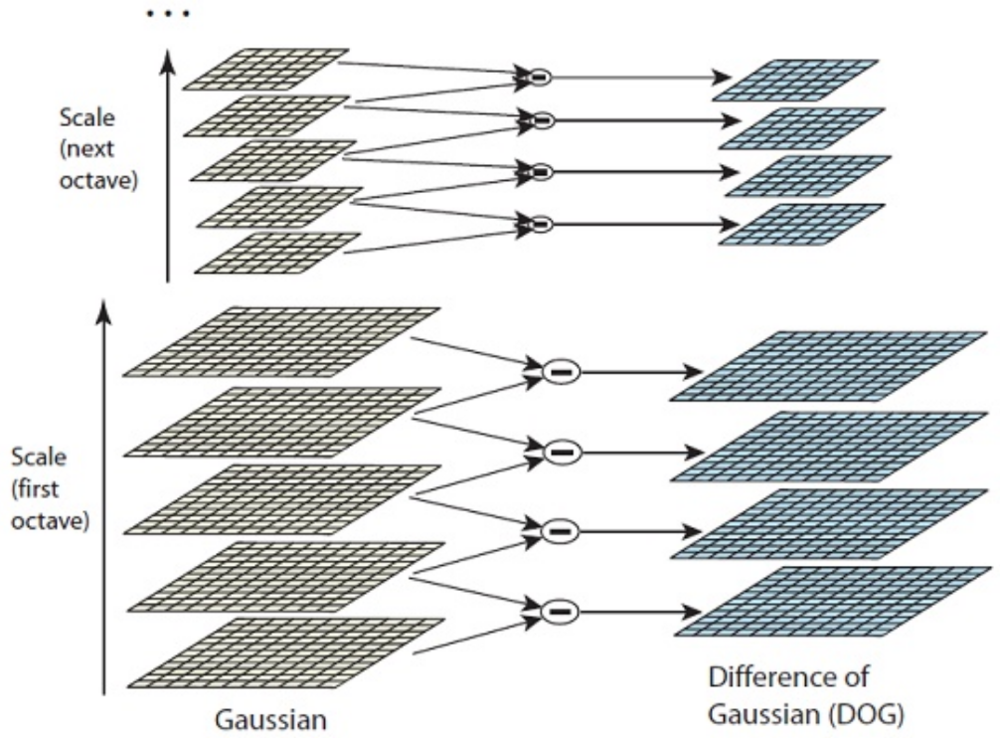DoGにおいて、 二つ目の工夫. ガウシアンのσを大きくしていき(kσ、k^2σ...)数回処理を実行するが、 一定回数を行ったのちには、 画像を縮小して再度σから大きくしていく(kσ、k^2σ)
上記のように複数のσでLoGの近似結果を求めることで、スケールに対して不変的な特徴を得ることができる/スケールがどれくらいか求められるようになります.
LoG
この章を学んで新たに学べる
Comments

Reasons
>>隠す

知識: LoG
LoG(Laplacian of Gaussian)はガウシアンフィルタによって先にノイズを除去したのちにラプラシアンフィルタをかけることでエッジを抽出するフィルタです.用途としては、エッジの抽出やブロブの検出等が行えます.