-
 @ThothChildren
@ThothChildren
- 2018.9.17
- PV 675
LoG
ー 概要 ー
LoG(Laplacian of Gaussian)はガウシアンフィルタによって先にノイズを除去したのちにラプラシアンフィルタをかけることでエッジを抽出するフィルタです.用途としては、エッジの抽出やブロブの検出等が行えます.

この章を学ぶ前に必要な知識
条件
- 画像が入力のフィルタ
効果
- ノイズを抑えてエッジ抽出
- 特定の大きさのブロブを検出(σの大きさを調整して検出サイズ変更)
解 説
LoG(Laplacian of Gaussian)はガウシアンフィルタによって先にノイズを除去したのち(平滑化)にラプラシアンフィルタをかけることでエッジを抽出するフィルタです.
用途としては、大きく
・エッジの抽出
・ブロブの検出
等が挙げられます. | LoG(Laplacian of Gaussian)とは |
LoGのフィルタは以下のような式で表現されます.ガウンシアンフィルタの式とラプラシアンから用意に導出することができます.
$$f_{LoG}(x, y) = \frac{x^2+y^2-2\sigma^2 }{2\pi \sigma^6}exp(-\frac{x^2+y^2}{2\sigma^2})$$
実際にフィルタを使う時には\(\sigma\)の値は決めたからフィルタを使います.ガウシアンフィルタと同様に、\(\sigma\)の値を大きくしたら大きくぼかした画像に対してエッジを求めることになり、\(\sigma\)の値を小さくしたら元の画像と近いままエッジを求めることになります. | LoGについて |
画像に対してガウシアンフィルタをかけることで画像をぼやかした状態にする(ノイズを低減しているとも言う).さらにそれにラプラシアンフィルタをかけることでエッジを抽出していることは既に述べました.当然そのようなノイズに強いエッジ抽出としての役割もありますが、もう一つLoGには大切な役割があります.
「特定サイズのブロブの検出」です.
LoGは以下のような曲線となっており、中央が1で、その周辺(半径σより外側)が0になっている領域に最大の値を与えます.これを利用するとσの大きさの円形を検出することが可能になります.
σはブロブの半径Rの半分になるため,
$$\sigma = \frac{R}{2}$$
となります.
特定の大きさを見つけたい時 → σを固定して画像全体にフィルタを掛けて最大値を探す.
ブロブがどのくらいの大きさか知りたい時 → 画像にσの値を変えながらフィルタを掛けてみる.一番大きくなった値が適切なスケール値(σ)になっている. | LoGによるブロブの検出について |
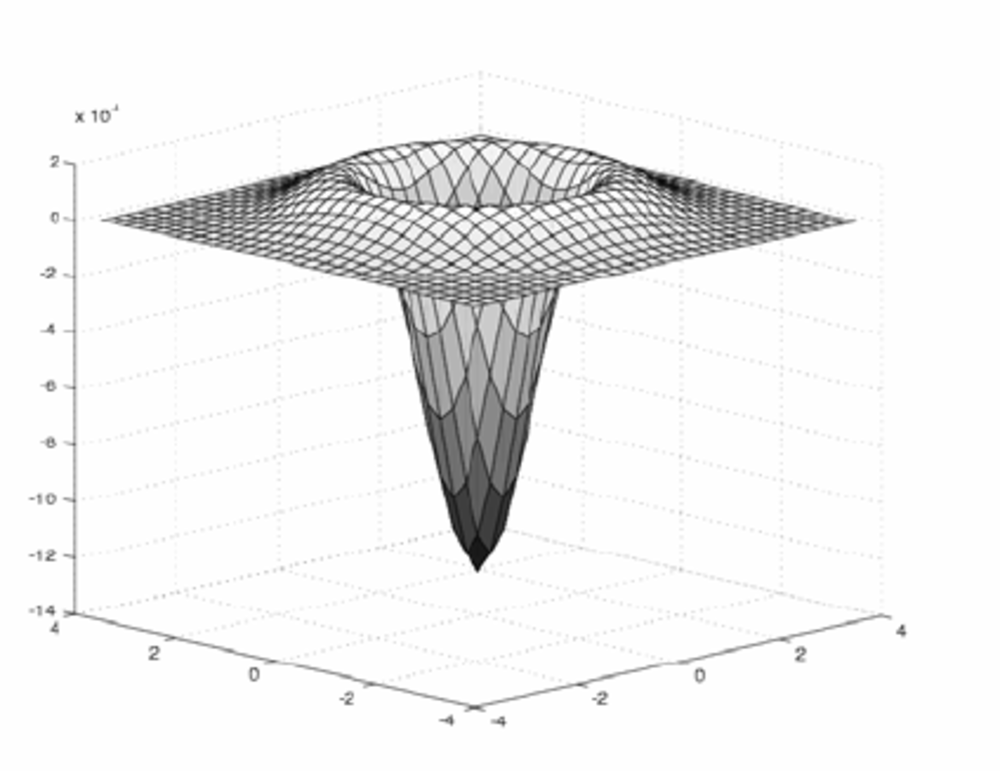 | LoGを可視化したグラフ.
これらを掛け合わせてフィルタ処理を行う. |
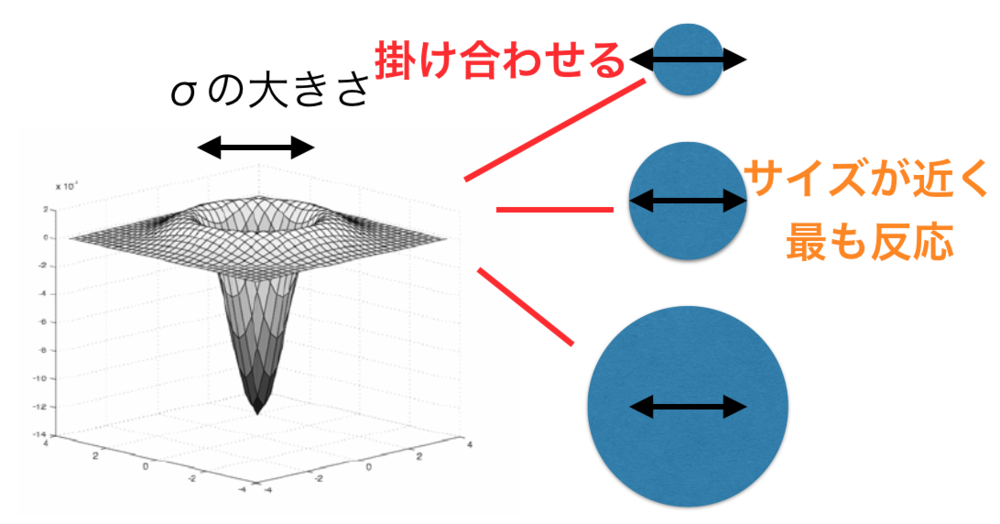 | LoGと画像に映る各サイズの円と掛け合わせると、
サイズが一致しているものが最も反応する. |
この章を学んで新たに学べる
Comments


