ベクトルを特定の平面に射影したい

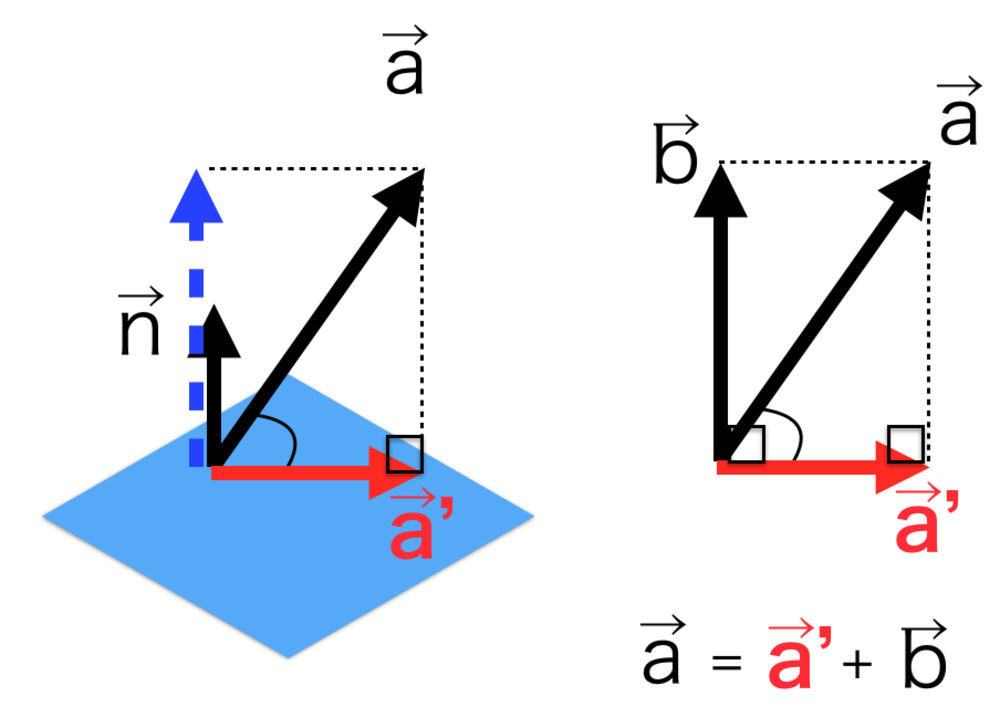
ベクトルをある平面に射影する方法についてまとめています. ベクトルAをある平面に射影するには、以下のように行います. 法線ベクトルnとする. 方法概要 1. 平面の法線ベクトルnに対象のベクトルAを射影します.(それをベクトルBとする) 2. 法線成分をベクトルAから取り除くために、ベクトルAからベクトルBを引きます.

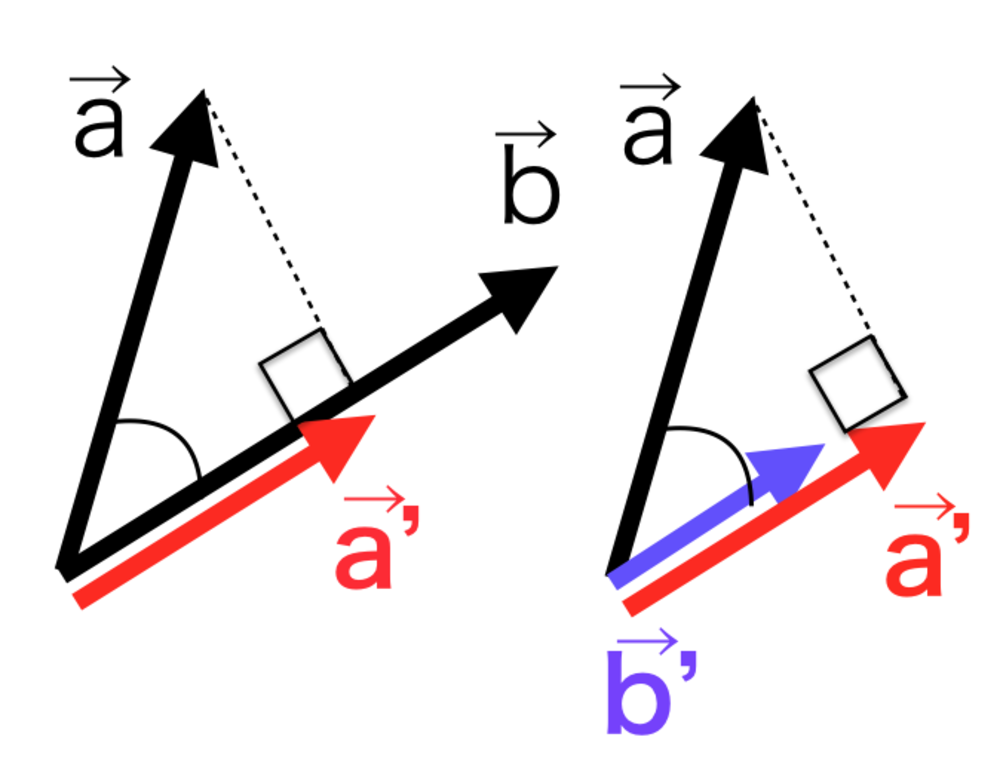
ベクトルを別のベクトルに射影する方法については、リンクを参照してください.

与えられたベクトルAと平面の法線ベクトルnから射影したベクトルBを求めます. $$\vec{B} = (\vec{A}\cdot\vec{n}) \vec{n}$$ この\(\vec{B}\)は\(\vec{A}\)の平面に垂直な成分です. この成分を元のベクトル\(\vec{A}\)から引きます. $$\vec{A'} = \vec{A} - \vec{B}$$ この\(\vec{A'}\)が射影したベクトルです.