-
 @ThothChildren
@ThothChildren
- 2018.8.5
- PV 4276
ベクトルを別のベクトルに射影したい
ー 概要 ー
特定のベクトルを他のベクトルに射影する方法についてまとめたページです.ベクトル同士の内積を行うことで簡単に求めることができます.
この章を学ぶ前に必要な知識
条件
- 同一の次元数の二つのベクトル
効果
- ベクトルをある方向に射影したベクトルを算出
ポイント
- 求めたいベクトルは片方のベクトルを数倍した大きさである
解 説
ベクトルを別のベクトルに射影したいときに使える手法について紹介します.
このベクトルは空間ベクトル(3次元)でも平面ベクトル(2次元)でも構いませんし、もっと次元数(n次元)の大きなベクトルでも同様です.
ベクトルを他のベクトルに射影するとは
あるベクトルAを別の方向につまり別のベクトルBに射影した時、
最終的に得られるベクトルは当然射影をしているのですからベクトルBと同じ方向です.
つまり、射影したベクトルはベクトルBと同じ方向 = ベクトルBを何倍かしたベクトル
ということになります.このベクトルBを何倍したかを求めることが今から行う計算です. | ベクトルを別のベクトルに射影したいとは |
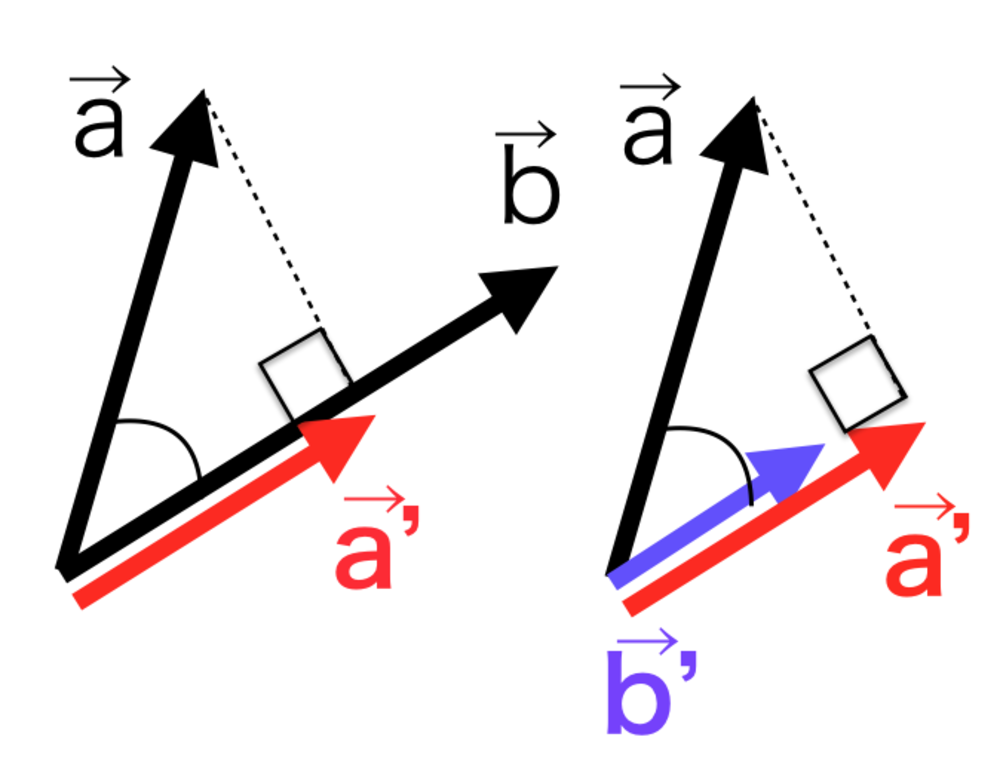
 | ベクトルA' が射影したベクトル.
これをベクトルAとベクトルBを使って求めたい.
求めたいベクトルA'は当然ベクトルB'と同じ方向を向いている. |
解く問題の整理をもう一度行います.
\(\vec{a'}\)が今回求めたい射影したベクトルです.上の話からこれはs倍した\(\vec{b}\)またはt倍した単位ベクトル(大きさが1のベクトル)\(\vec{b'}\)で以下のように書けます.このようにかけるのは射影したベクトルが\(\vec{b}\)や\(\vec{b'}\)と並行だからです.
$$\vec{a'} = s\vec{b} = t\vec{b'}$$
| いまから解く問題 |
さて、どうやってsまたはtを求めるかです.
射影しているので、\(\vec{a}\)と\(\vec{a'}\)のなす角\(\theta\)を使って以下の式が成り立ちます.
$$|\vec{a'}| = |\vec{a}| cos\theta $$
これは上の図からも明らかです.
ここでベクトルの内積が\(\vec{x}\)と\(\vec{y}\)を使って以下のようにかけることを利用します.
$$\vec{x} \cdot \vec{y} = |\vec{x}||\vec{y}|cos\theta $$
このときに\(\vec{y}\)の大きさ\(|\vec{y}|\)が1だったなら(yが単位ベクトルなら)以下のように簡単になります.
$$\vec{x} \cdot \vec{y} = |\vec{x}|cos\theta $$
これは先ほどみたベクトルaの式と同様です.
つまり、同様に考えれば\(\vec{a}\)と\(\vec{b}\)を使って以下のようにすることで\(\vec{a'}\)の大きさがわかり、単位ベクトル\(b'\)にその大きさをかければ\(\vec{a'}\)が求まります.
$$\vec{a} \cdot \vec{b'} = |\vec{a}|cos\theta =|\vec{a'}|$$
もし単位ベクトルにする前の\(\vec{b}\)を使うなら
$$\frac{\vec{a} \cdot \vec{b}}{|\vec{b}|} = |\vec{a}|cos\theta =|\vec{a'}|$$
となります.
単位ベクトル\(\vec{b'}\)が上記の大きさになったものが求めたい射影ベクトルなので、
$$|\vec{a'}| = \frac{\vec{a} \cdot \vec{b}}{|\vec{b}|} \vec{b'} = \frac{\vec{a} \cdot \vec{b}}{|\vec{b}|^2 }\vec{b} $$
| 解き方 |
この章を学んで新たに学べる
Comments


