-
 @ThothChildren
@ThothChildren
- 2018.7.15
- PV 259
画像の2次微分
ー 概要 ー
画像の2次微分も画像の1次微分と同様な考えで計算を行います.隣接画素の足し算引き算によって2次微分は計算することが可能です.
この章を学ぶ前に必要な知識
効果
- 画像の2次微分を算出
ポイント
- 画素同士の足し算引き算によって算出
解 説
以下の解説は、画像の1次微分がベースとなっているのでリンクを貼っておきます. | 画像の1次微分 |
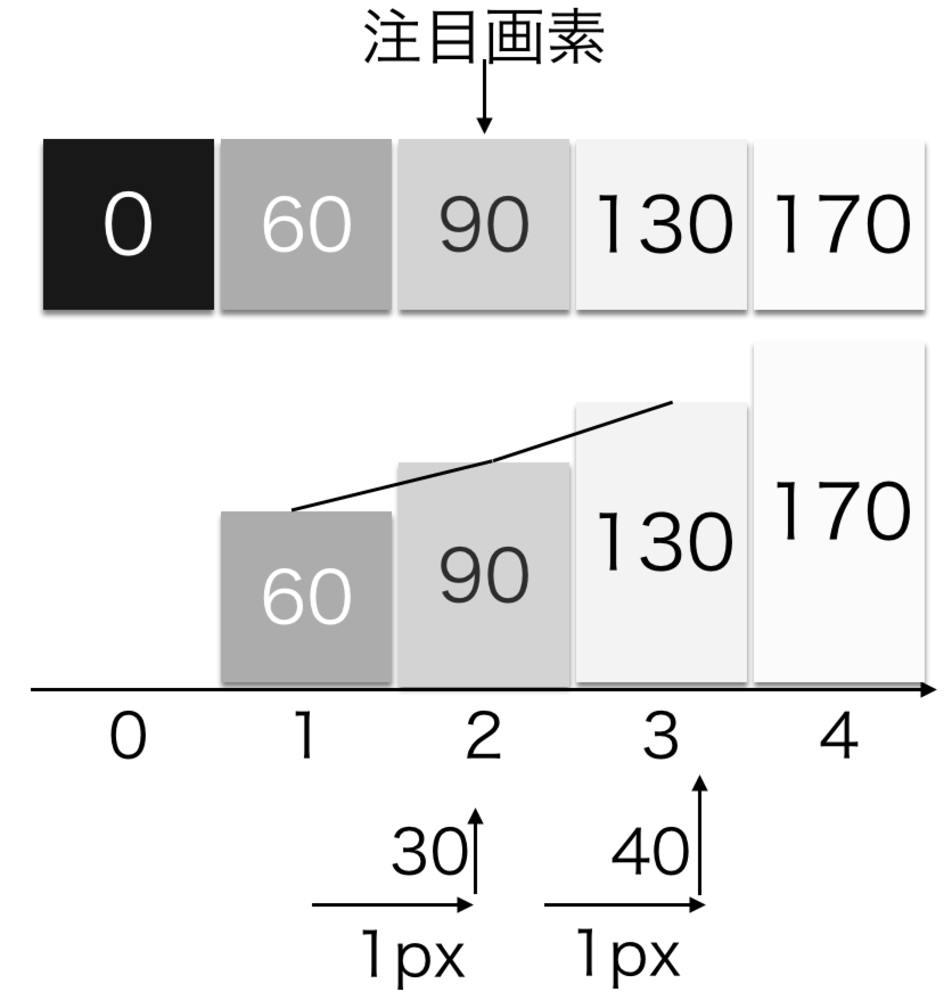
画像の2次微分では、注目画素の近隣画素を使用しながら求めることができます.
一次微分のときのように数式で表せれば、
$$f''(x) = \lim_{h \to 0}\frac{f'(x+h)-f'(x)}{h}$$
と表すことができます.
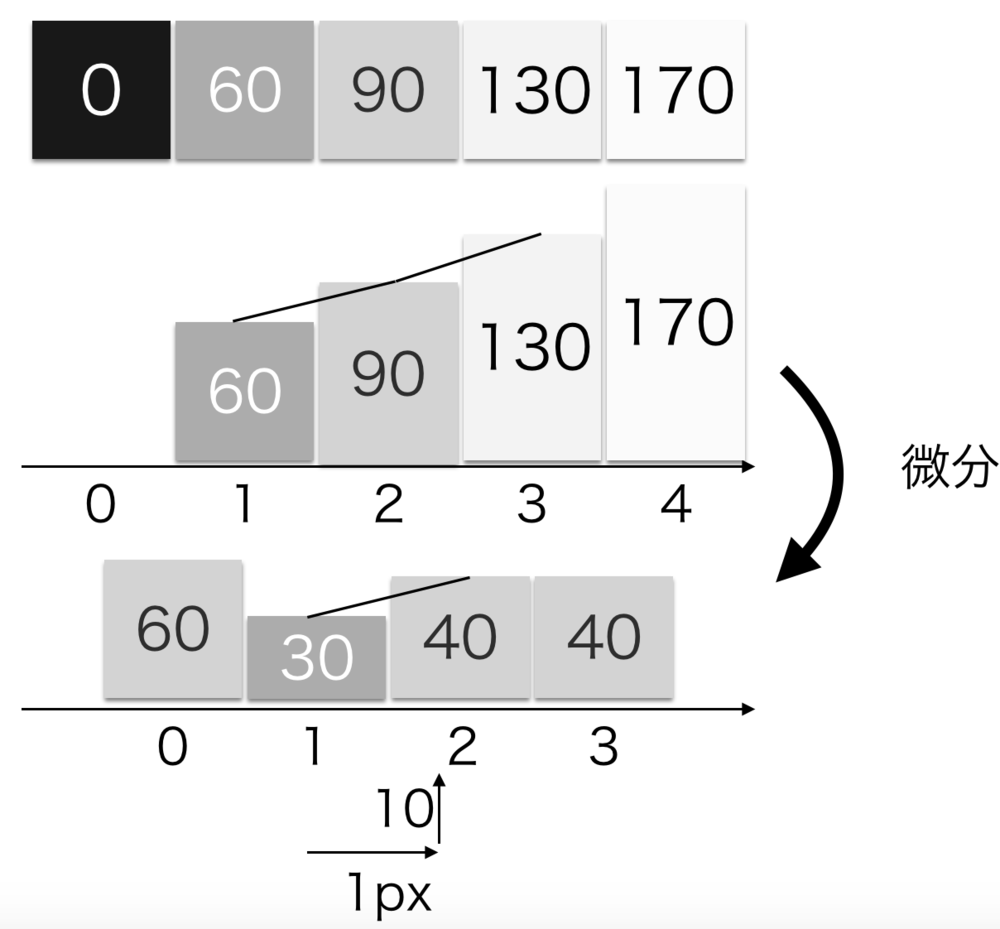
1次微分のときは、隣接した画素と引き算することだけで求まったので同様に考えれば、
x方向の2次微分は
$$I_{xx}(x,y) = \frac{I_{x}(x+1,y) - I_x(x,y)}{1}\\
= (I(x+1,y)-I(x,y))-(I(x,y)-I(x-1,y))\\
= I(x+1,y)+I(x-1,y)-2I(x,y)$$
y方向の2次微分も同様にして
$$I_{yy}(x,y)
= I(x,y+1)+I(x,y-1)-2I(x,y)$$
| 画像の2次微分について |
下記のような画像において2次微分を計算を行う.
$$I_{xx} = 130 + 60 - 2 \times 90 = 10$$
$$I_{yy} = 100 + 70 - 2 \times 90 = -10$$
と求まる | 画像の2次微分計算例 |
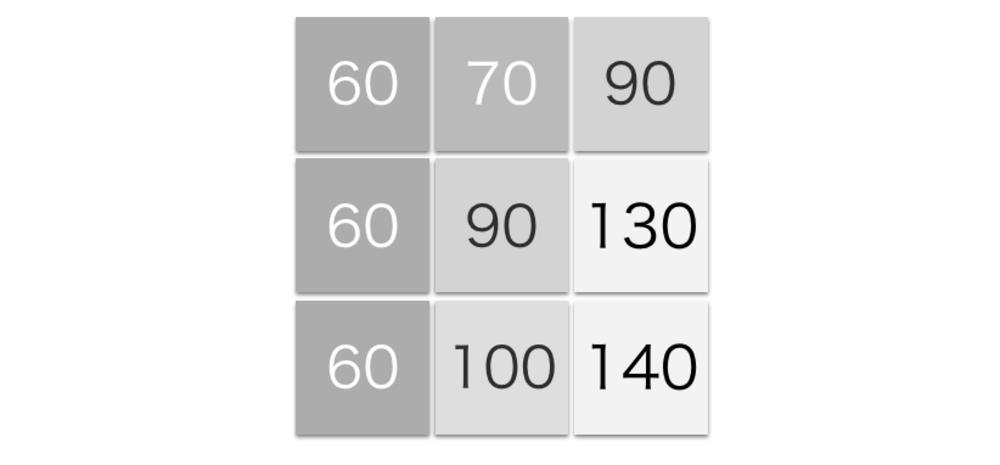 | 画像の2次微分の例 |
この章を学んで新たに学べる
Comments