この章を学ぶ前に必要な知識
条件
- 画像が入力
効果
- 画像の微分を計算
ポイント
- 画像の輝度は通常Iで表され、Ixがx方向の微分、Iyがy方向の微分を表す
解 説
画像の微分はコーナー検出やエッジ検出など様々な局所的な計算をする上で必要になります.ここではその計算方法についてまとめています.
そもそもですが、微分の計算は以下です.
$$f'(x) = \lim_{h \to 0 }\frac{f(x+h)-f(x)}{h}$$
これは微小に変化したf(x)を微笑に変化させた量で傾きを求める計算でした.
どうようのことを画像で行うとなると以下のようになります.
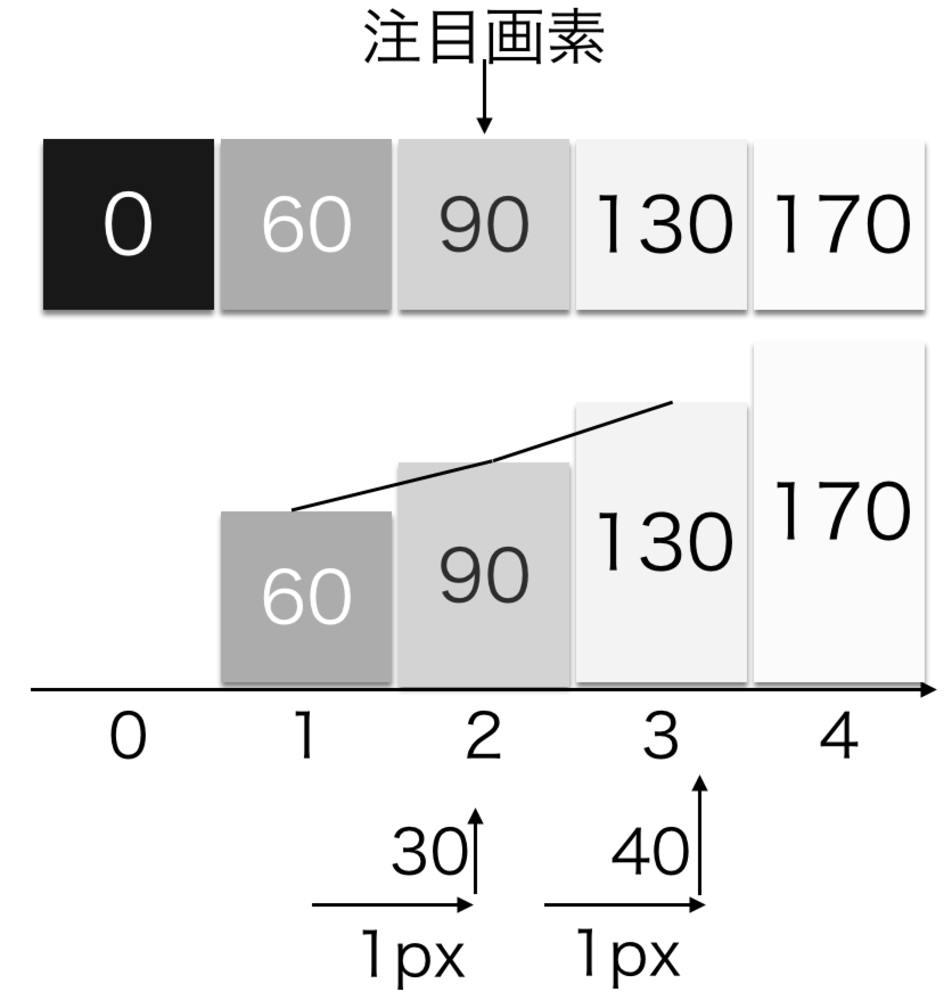
まずx方向について考えると | 画像の1次微分について |
 | 注目画素xはf(x)=90
注目画素の両隣はf(x+1)=130,でf(x-1)=60とここではなります.
画像は多分にノイズを含みやすいため,完全に隣接したf(x+1)とf(x)ではなくf(x+1)とf(x-1)を使用します. |
一番小さい移動量は1pxになります.そしてその前後の増減量は\(f(x+1, y)-f(x1, y)\)または\(f(x, y)-f(x-1, y)\)によって求めることができます.
1pxで上記の増減量があるため、x方向の微分値を\(I_x\)とすると
$$I_x = \frac{f(x+1, y)-f(x, y)}{1}=f(x+1, y)-f(x, y)$$
となります.
しかし、通常画素にはノイズが乗るため、両隣の傾きの平均をとって求めることが多く.
$$I_x = \frac{f(x+1, y)-f(x, y) +f(x, y)-f(x-1, y) }{2}\\
=\frac{f(x+1, y)-f(x-1, y) }{2}$$
と計算します.
同様にyの微分\(I_y\)は
$$I_y =\frac{f(x, y+1)-f(x, y-1) }{2}$$
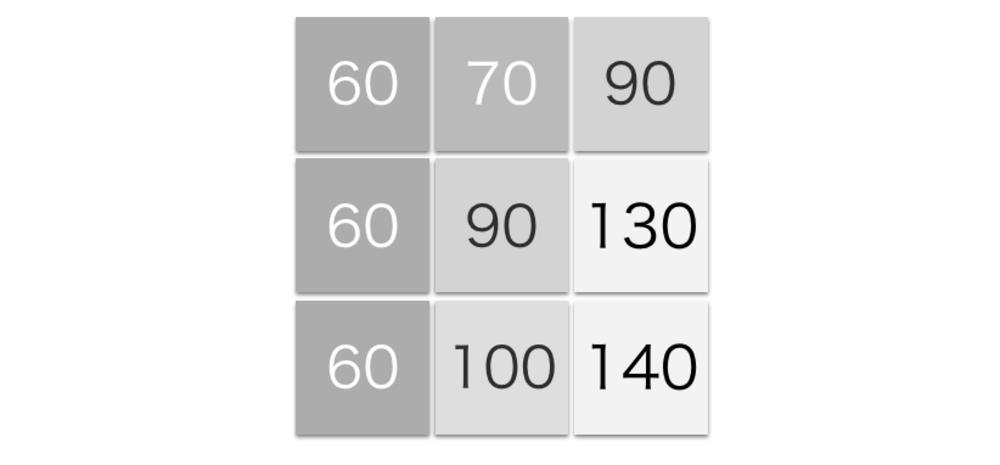
| 画像の1次微分の計算 |
以下のような画像の場合は、
$$Ix = \frac{130-60}{2} = 35$$
$$Iy = \frac{100-70}{2} = 15$$
と求まります. | 1次微分の計算例. |
 | 1次微分の画像例 |
この章を学んで新たに学べる
Comments
 @ThothChildren
@ThothChildren


