-
 @ThothChildren
@ThothChildren
- 2018.6.26
- PV 204
可能な限り正確に等高線を可視化したい
ー 概要 ー
ある関数の出力を一定になるように入力変数を変更するとき、その等高線を可視化する方法について紹介します.二変数を入力に1出力する関数において等高線を一つ描画することを前提に考えます.
この章を学ぶ前に必要な知識
条件
- x,yの2入力でzの一出力z=f(x,y)
- f(x,y)が微分可能
- 等高線を延ばす刻みステップ幅を決めておく
- 最初の点を与える(等高線上になくてもよい
- 最適化の閾値
効果
- c=f(x,y)の等高線を得る
ポイント
- f(x,y)=cを満たす点を一点ずつ見つけてくことで等高線を描く
- f(x,y)=cを満たす点はNewton法などの最適化手法によって求める
解 説
可能な限り正確に等高線を可視化する方法についてまとめたページになります.
ここでは2入力x,yを受け取りzを出力するようなz=f(x,y)の等高線の描画を想定しています.定数cとしてc=f(x,y)を満たすx,yの等高線を描く. | 可能な限り正確に等高線を可視化したい |
もし厳密でなく何となくな位置を簡単に求めたい場合は、
右の知識を参照 | 不正確でも単純な等高線を可視化したい |
1.y=g(x)と書き直せる場合 | |
c=f(x,y)の関数を変換することでy=g(x)に書き直せる場合は、とてもシンプルに等高線を描くことができる.yの値を求めつつxの値を小さい値から大きくしていくことで、等高線が完成する.
例えば, 1=f(x,y) = y+xのような場合などが上げられる.この場合やy=-x+1として、xの値を変えながら描画すればよい. | y=g(x)に書き直せる場合 |
2.複雑なためc=f(x,y)から変形しにくい場合 | |
先ほどのようにy=g(x)と書き直せない場合は、少し厄介になる.
このときは率直に等高線上の点を求められなくなるため、最適化手法を用いて満たす点を探索するほかない.
方針
そのため、基本的な方針は以下のようになる.
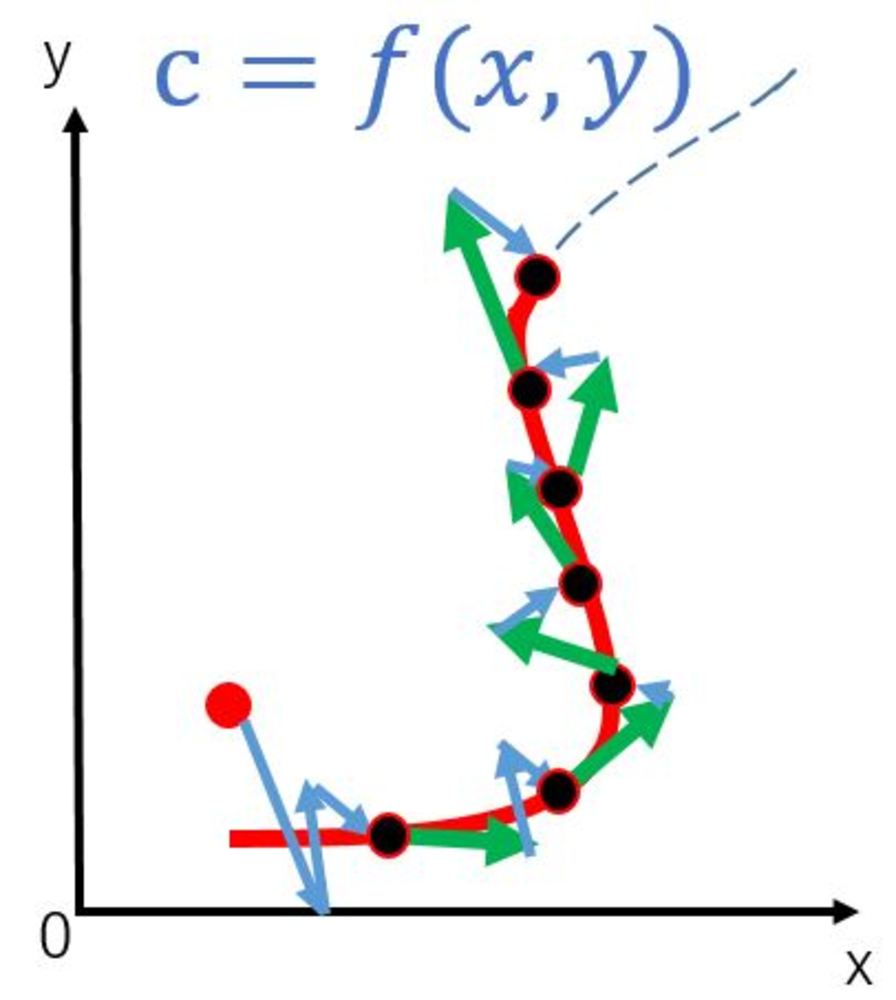
1. 点を与える.
2. 与えられた点を起点に等高線上の点を最適化で見つけ出す.
3. 等高線上の点が見つかればその点を等高線を描くための点として保持する.
4. 3.の点から指定したステップ幅はなれた点を与えて2.から繰り返す. | c=f(x,y)から変形が難しい場合 |
上記のような方針を進める中で、
2.の最適化ではNewton法等による手法で、点の位置を少しずつ更新しながら等高線上の適切な点を見つけ出すことになる.
ステップ幅と最適化の誤差の許容閾値次第で等高線の正確さが決まる. | 最適化に関して |
この章を学んで新たに学べる
Comments
Reasons
知識: 不正確でも単純な等高線を可視化したい
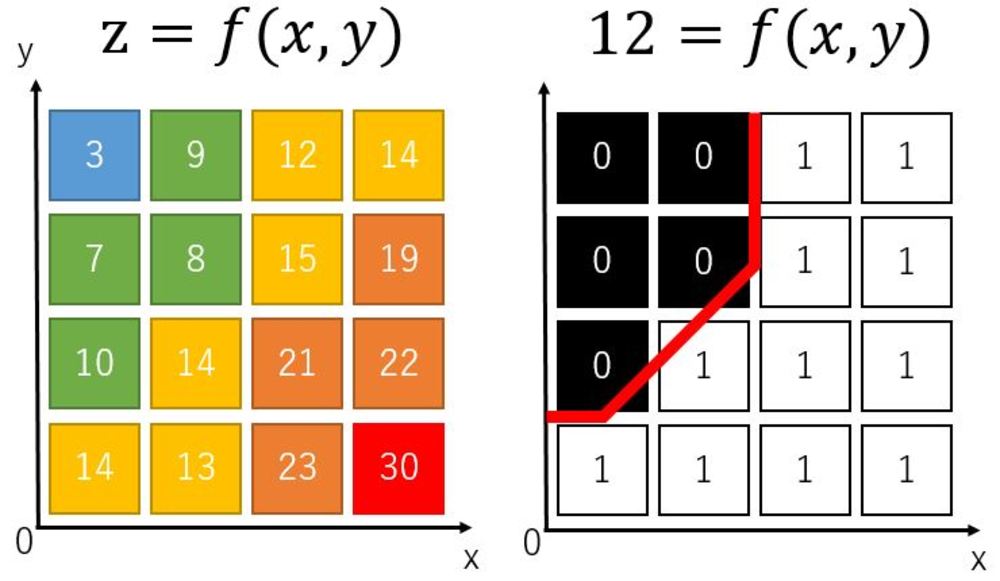
2Dグラフ上で間接的にでも関数の出力が同じになっている場所がどこなのか可視化したいときの手法についてまとめます.ここでは等高線そのものを可視化することはなく、入力の範囲内で全ての関数の出力値を求めて描画します.


