不正確でも単純な等高線を可視化したい

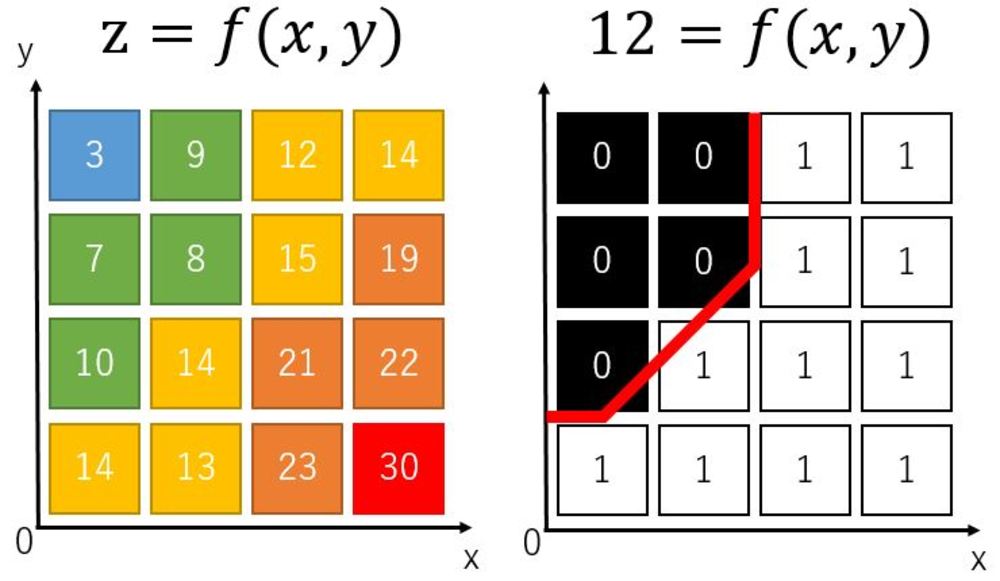
不正確でも単純な等高線を可視化する方法についてまとめた手法です. 注意ですが、 ここでは等高線を直接描画はしません. あくまで、全体の値を可視化することで等高線がどこにあるのか目で見れるようにするということにとどまります.どちらかと言えば「f(x,y)の出力をカラーにしたい」という方が正確かもしれません。 大まかな方針は、 x,yのサンプリングを行って各箇所での値を取得して、 それに適度な色をつけて描画します. 手順 1. x,yをどの程度の間隔でサンプリングするか決定 2. x,yの各点でのf(x,y)を算出 3. f(x,y)の出力値と求めたい等高線の値cとの差分で閾値処理.cより大きければ1,小さければ0. 4. グラフ上にて3.の出力値を元にMarching squaresなどを行いながら描画していく.

1.の工程では描画したい細かさに沿って、x,yのサンプリングする間隔を決定します. 時間は分割した数に比例して増えていくので注意です. 2.に関しては特に問題なく、1.で決めたサンプリングの間隔に合わせて全て計算していきます.グリッドサーチの要領で全てのx,yの組み合わせを計算します. 3.は2の工程で求めた値と求めたい等高線の値の比較を行うだけなので、ここも簡単です. 最後の4.の工程は上記にて引用したMarching Squaresを行うことで容易に描画することができます.