シンプルに逆行列を求めたい

シンプルに逆行列を求める方法についてまとめます. 正則行列は逆行列を持ち、 逆行列が存在する必要十分条件は行列の行列式が0でないことです. ここでは主に以下の手法について紹介します. ・掃き出し法 ガウスの消去法またはガウス・ジョルダン消去法とも言われる.(厳密には異なる) LU分解より計算が多くなるため、逆行列を求める場合通常こちらは使われない.最も基本的な手法. ・余因子行列による方法 ランクが低い行列で使用する分には使える.ランクが高い行列では計算が大変になる. ・LU分解による方法(コレスキー分解による方法) 上三角行列や下三角行列から逆行列が求めやすいことを利用.O(n^2)で解ける

掃き出し法は行同士を足したり引いたりすることで、逆行列を求める手法です.

$$Ax = y = Ey$$ $$ \begin{eqnarray} \left( \begin{array}{rrr} 1 & 7 & 11 \\ 2 & 5 & 4\\ 3 & 9 & 6 \end{array} \right) \end{eqnarray} \left( \begin{array}{c} x_1 \\ x_2 \\ x_3 \end{array} \right) = \left( \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{c} y_1 \\ y_2 \\ y_3 \end{array} \right) $$ $$ \begin{eqnarray} \left( \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{c} x_1 \\ x_2 \\ x_3 \end{array} \right) = A^{-1} \left( \begin{array}{c} y_1 \\ y_2 \\ y_3 \end{array} \right) \end{eqnarray} $$

逆行列の各要素は、余因子を行列式で割ったものであるという性質を利用して、逆行列の各要素を一つずつ計算していきます.

余因子はi行j列目に注目しているときに与えられている行列Aからi行目の全要素とj行列の全要素を削除して得られる行列の行列式です. 余因子の算出後は行列全体の行列式で割って、逆行列を求めるのみです.

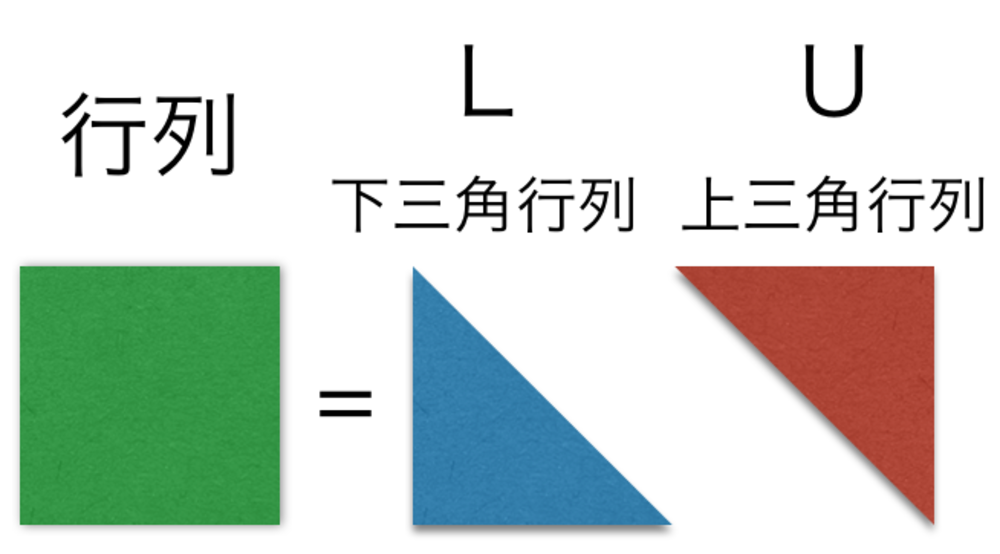
行列を上三角行列と下三角行列に分解することで、それらの逆行列を求めて、もともと求めたかった行列の逆行列を求めます. 上三角行列や下三角行列は容易に逆行列を求めることが可能です. LU分解の方法は右のリンクで確認してください.

$$A=LU$$ $$I=AA^{-1}=(LU)(LU)^{-1}$$ $$A^{-1}=U^{-1}L^{-1}$$