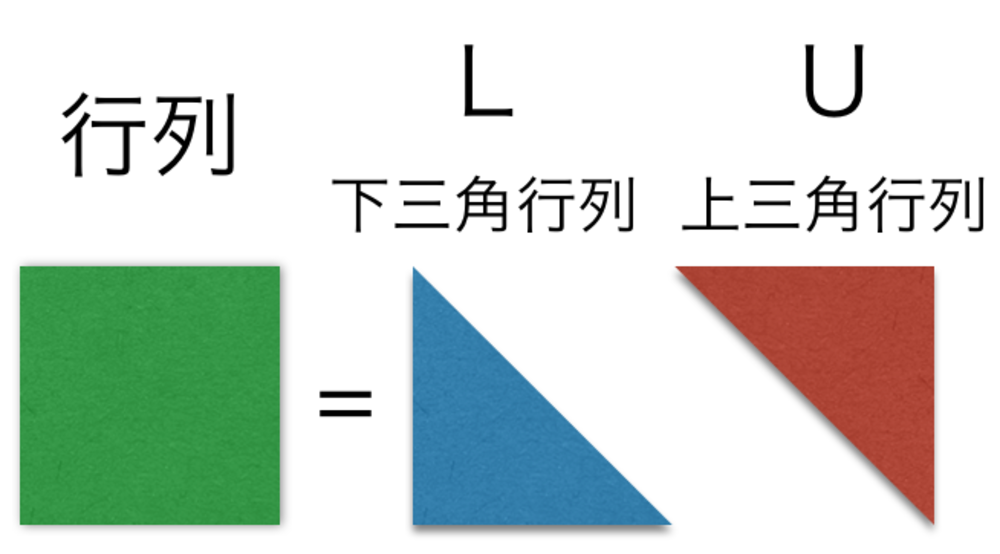
行列を分解して上下三角行列が欲しい

与えられた行列を分解して上三角行列と下三角行列を求めたいときの手法についてまとめる. 有名な手法としてLU分解(及びLUP分解. LU分解の特殊な形)がある. LU分解が可能な行列は限られていて容易な判断としては以下があげられる. LU分解またはLUP分解可能な行列 ・正方行列AはLUP分解可能. ・正方行列Aがさらに逆行列を持ち全ての主小行列式が非ゼロで逆行列がある場合,LU分解可能. ・正定値対称行列ならLU分解可能. またLU分解の特殊な形であるコレスキー分解は以下の条件で可能か判断できる コレスキー分解可能な行列 ・正定値対称行列

上記には書かなかったが、LU分解可能であることの必要十分条件に関して記述されている論文のリンクを右に記しておく.

上記の条件を守ったLU分解は以下の連立方程式を容易なものから解いていくことで実現することができる. Lの対角要素を全て1と仮定している.

$$A=LU$$ $$\begin{eqnarray} \left( \begin{array}{cccc} a_{ 11 } & a_{ 12 } & \ldots & a_{ 1n } \\ a_{ 21 } & a_{ 22 } & \ldots & a_{ 2n } \\ \vdots & \vdots & \ddots & \vdots \\ a_{ m1 } & a_{ m2 } & \ldots & a_{ mn } \end{array} \right)=\left( \begin{array}{cccc} 1 & 0 & \ldots & 0 \\ l_{ 21 } & 1 & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ l_{ m1 } & l_{ m2 } & \ldots & 1 \end{array} \right)\left( \begin{array}{cccc} u_{ 11 } & u_{ 12 } & \ldots & u_{ 1n } \\ 0 & u_{ 22 } & \ldots & u_{ 2n } \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & u_{ mn } \end{array} \right) \end{eqnarray} $$

$$a_{11} = u_{11}$$ $$a_{12} = u_{12}$$ $$\dots$$ $$a_{mn}=u_{1n}l_{m1}+\dots+u_{mn}$$

LU分解及びLUP分解はガウスの消去法と等価な計算.

正方行列で対角要素が0になった場合には、LU分解ができなくなってしまいます.そこで転置行列Pを求めることで正方行列ならいつでも分解できるようにします.

$$PA=LU $$

置換行列Pの求め方ですが、プログラムで解くときには直接求めることはしません. 左から列に注目していき、各列で最大の値が上にくるように行を交換することでPAを求めます. もちろんその結果からPを求めることは可能です.

$$\begin{eqnarray} A=\left( \begin{array}{rrr} 4 & 11 & 6 \\ 5 & 2 & 3 \\ 3 & 1 & 9 \end{array} \right) \end{eqnarray} $$ $$\begin{eqnarray} A'=PA=\left( \begin{array}{rrr} 5 & 2 & 3 \\ 4 & 11 & 6 \\ 3 & 1 & 9 \end{array} \right) \end{eqnarray} $$ $$\begin{eqnarray} P=\left( \begin{array}{rrr} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{array} \right) \end{eqnarray} $$

これスキー分解では以下のように分解できることを想定しており、 LU分解に置けるUをL^tに置き換えたにすぎません. なので平方根等を用いること以外、通常通り計算することができます.

$$A=LL^{ \mathrm{ T } }$$

$$L_{j,j}=\sqrt{A_{j,j}-\sum_{k=1}^{l-1}L_{j,k}^2}$$ $$L_{i,j}=\frac{1}{L_{j,j}}\sqrt{A_{i,j}-\sum_{k=1}^{l-1}L_{i,k}L_{j,k}}$$