-
 @ThothChildren
@ThothChildren
- 2018.6.14
- PV 358
Jaccard類似度でベクトル間類似度を求める
ー 概要 ー
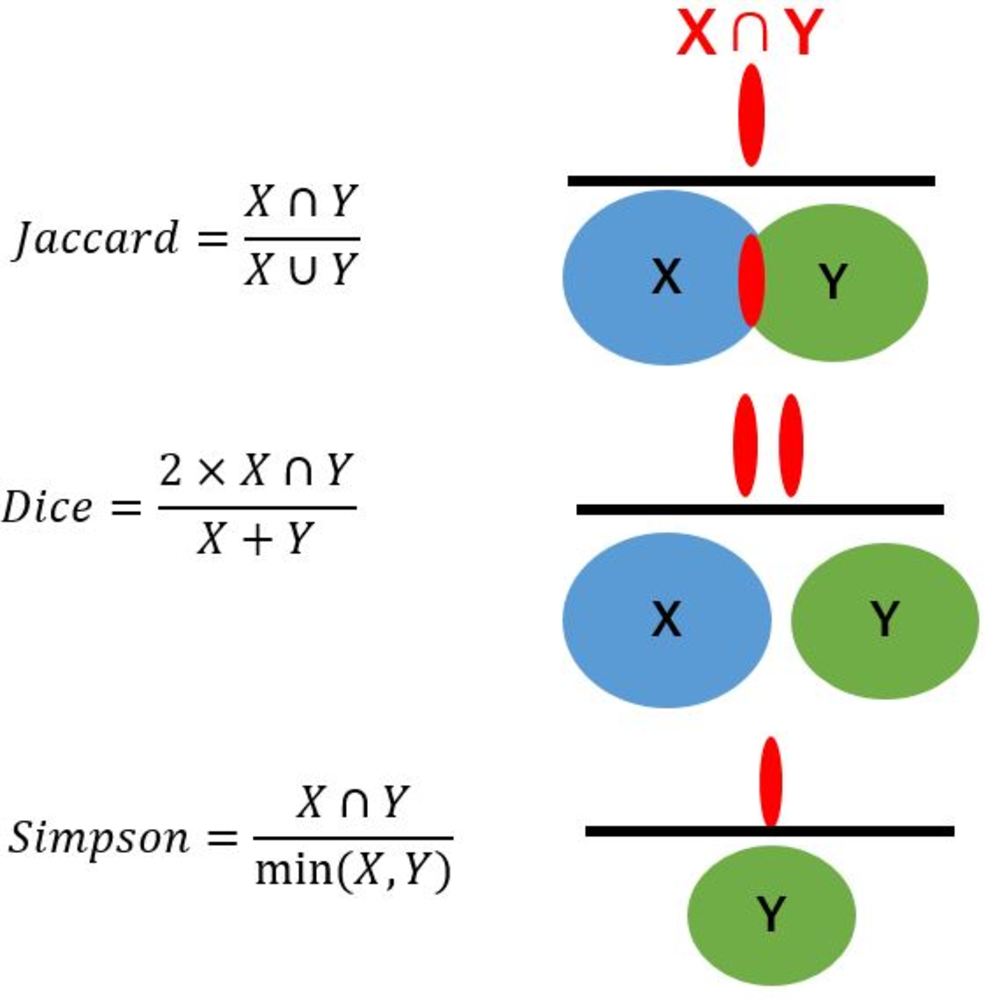
Jaccard類似度を使ってベクトル間距離を求める方法について紹介します.Jaccard類似度は集合の類似度として使用されることが多いが、ベクトルに対しても使用できます.通常のJaccard類似度は全てのベクトルの要素が0または1である必要がある.
この章を学ぶ前に必要な知識
条件
- 二つのベクトルが入力
- 要素が1または0ならJaccard類似度
- 要素が1または0と限らないなら一般化Jaccard類似度
効果
- 二つのベクトルの類似度を求める
解 説
Jaccard類似度でベクトル間距離を求める方法についてまとめます.
Jaccard類似度はそもそも集合の類似度で定義されていた技術です. | Jaccard類似度でベクトル間距離を求める |
右のページに集合の類似度の定義が記述されています. | 集合内同一要素の数で類似度を測りたい |
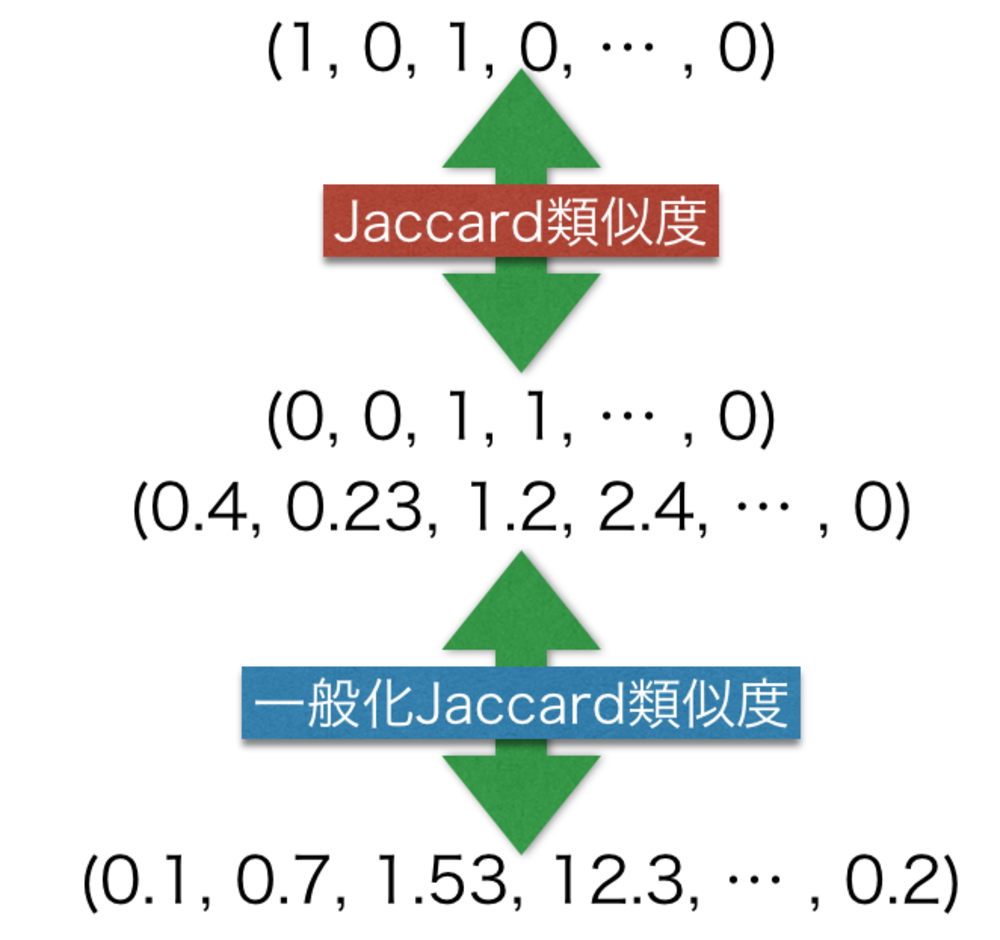
1.ベクトルの要素が0または1で構成されてる | |
ベクトルの要素が0または1で構成されている場合は、通常のJaccard類似度と同様の定義で計算することができます. | Jaccard類似度によるベクトル類似度の計算 |
$$Jaccard = \frac{|A\cap B|}{|A \cup B|}$$ | Jaccard類似度の定義 |
例えば\(\overrightarrow{ a }=(0,1,0)\)と\(\overrightarrow{ b } = (1,1,0)\)があるとき、以下のようになる.
$$Jaccard = \frac{|A\cap B|}{|A \cup B|} \\ = \frac{1}{2}$$ | Jaccard類似度の計算.
分母はベクトルaかベクトルbで1になっている数.
分子はベクトルaでもベクトルbでも1担っている数. |
2.ベクトルの要素が連続値の場合 | |
ベクトルの各要素の値が連続値の場合はそのままJaccard類似度を適用することはできないため、一般化Jaccard類似度を計算する必要があります. | 一般化Jaccard類似度の計算について |
$$Generalized Jaccard = \frac{\sum_{i}^n min(a_i, b_i)}{\sum_{i}^n max(a_i, b_i)}$$ | 分子が各要素の値の最小値の和で、分母が各要素の値の最大値の和.
完全に一致していれば1になります.隔たりが大きいほど値は小さくなります. |
例えば\(\overrightarrow{ a }=(0.2,0.6,0.3)\)と\(\overrightarrow{ b } = (1.0,1.2,0.1)\)があるとき、以下のようになる.
$$Jaccard = \frac{\sum_{i}^n min(a_i, b_i)}{\sum_{i}^n max(a_i, b_i)} \\ = \frac{(0.2+0.6+0.1)}{(1.0+1.2+0.3)} \\ = \frac{9}{25}$$ | 一般化Jaccard特徴量の計算 |
この章を学んで新たに学べる
Comments