-
 @ThothChildren
@ThothChildren
- 2018.5.15
- PV 835
全点通る滑らかな関数近似をしたい
ー 概要 ー
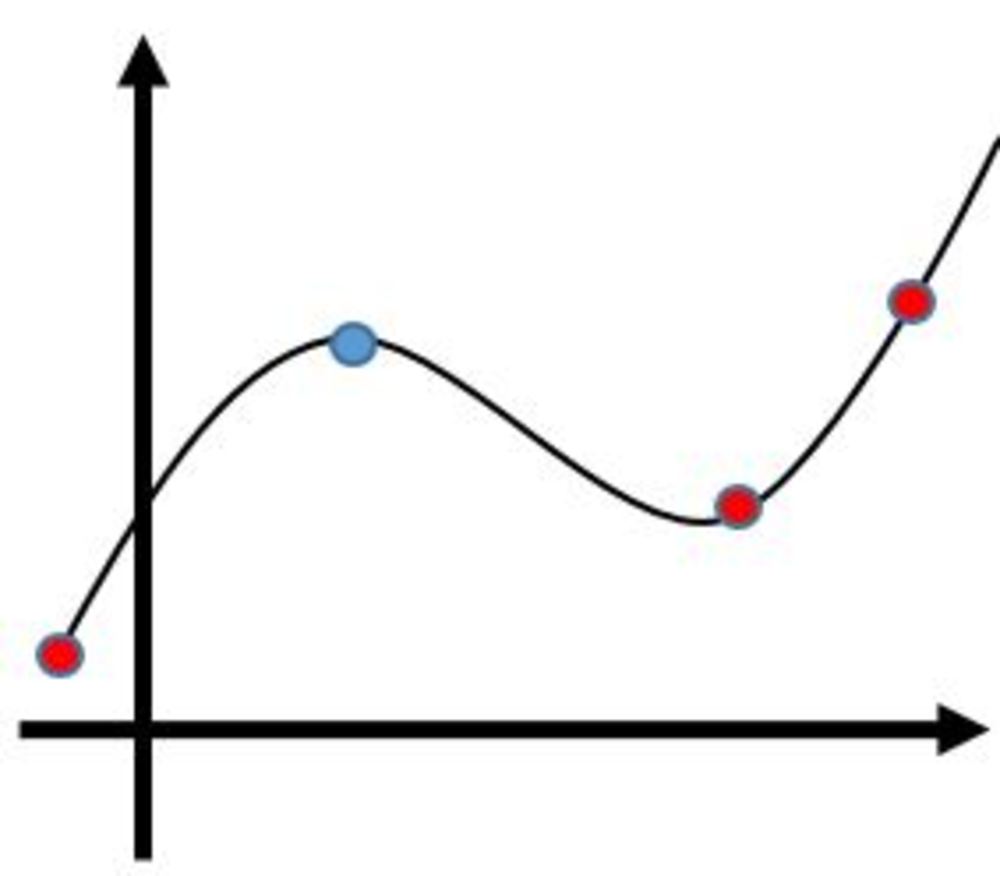
全点のデータを通りつつ滑らかな曲線による関数近似をする方法について記載します。多項式による近似を主に紹介します.
この章を学ぶ前に必要な知識
条件
- 通過したい2点以上の複数のデータ点
効果
- 全ての点を通った近似または補間関数を得る
ポイント
- 多項式による近似が主
- 設定次第では、点列にオーバーフィッティングする可能性が大いにあり
解 説
ここでは、複数のデータ点が与えられその全ての点を通る近似関数を推定する方法についてまとめます。近似とは行っていますが、補間に近いイメージでしょうか?
基本的な作戦は、複数の関数の足し合わせで滑らかな関数を作り出します。足し合わせるときにその係数をどのように求めるかなどが関数作成の際の主な作業になります。
主な方法は以下の通りです。
・多項式補間 (ラグランジュ補間、ニュートン補間)
・スプライン補間
・ベジェ補間
・カーネル法 | 全点を通る滑らかな関数近似の方法について |
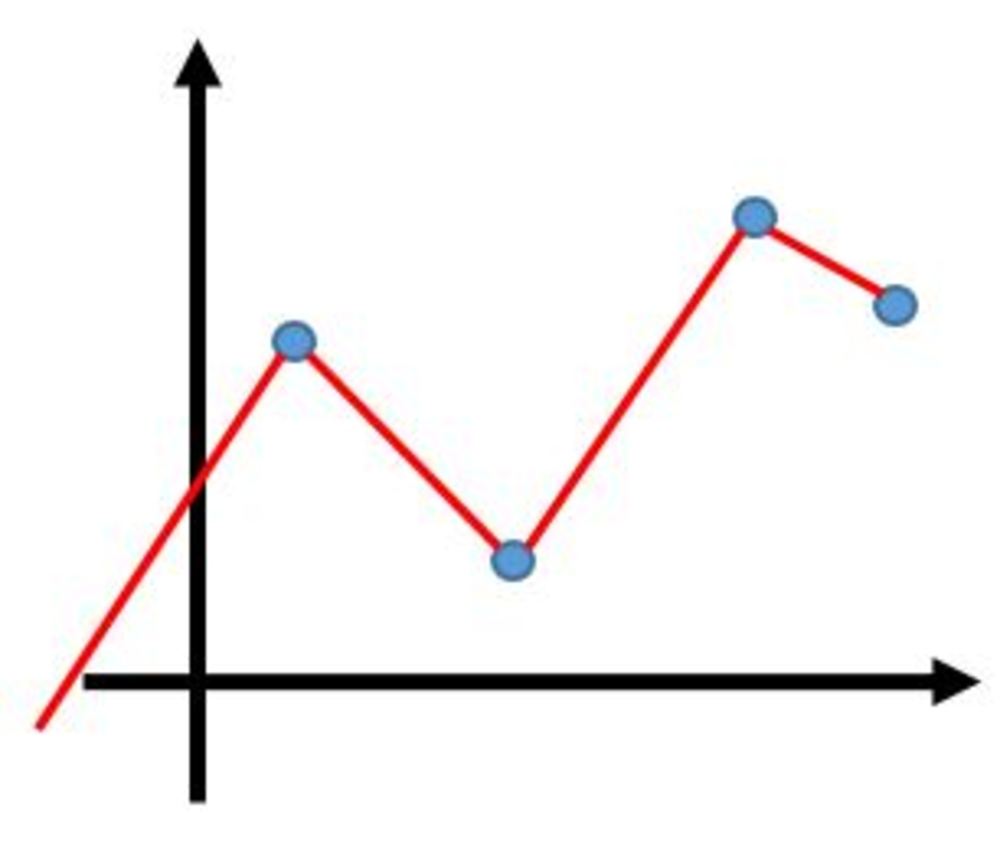
今回の方法では各データ点において傾きは連続になります。右のような折れ線関数等においては傾きは不連続になり、また関数を一つの式では表すことができません. | 全点通る滑らかでない関数近似をしたい |
1.単純な多項式補間 | |
多項式補間に関しては、「ルンゲ現象」の問題点が分かっており、それらを解消するのが、スプラインになります.
多項式補間の補間は結果的には一つの式に定まりますが、複数の算出方法があります.
実際の数値計算においては数値に誤差が乗ることで適切な値が出ないことがあるため、ラグランジュ補間またはニュートン補間を使用します。
そしてこれらはともにルンゲ現象になりうる補間となっています。
「ルンゲ現象」とは通常は補間点が多いほど精度がよくなるのに、特定の関数のときにおいて補間点が多いほど関数が暴れて誤差が大きくなるような現象のことを差します. | 多項式補間概要 |
1.1.ラグランジュ補間 | |
ラグランジュ補間を用いれば、指定した点を通る関数を得ることができます.
ラグランジュ補間では以下の式で表されるラグランジュ基底多項式の線形結合で表現されます.
このときの条件はどの点のxも同一ではないことです.
下の式でx = xpのときには、上の前提よりj=pのとき以外は全て0になるため、他の項は全てなくなるのがポイント | ラグランジュ補間概要 |
 | ラグランジュ基底多項式(Wikipediaより) |
 | 上記の多項式を重みとしてyjに掛け合わせた線形結合.これが多項式.
j = aのときを考えれば, la(x)はj=aのとき1となり、L(x) = yaとなり指定した点を通ることになる |
 | ラグランジュ多項式による補間例
両端において発散が見られるのはルンゲ現象によるもの |
ニュートン補間はラグランジュ補間と同様なものなので省略.
詳細はwikipedia参照 | 外部リンク ニュートン補間 Wikipediaより |
2.区間前後のみを参照してルンゲ現象のない補間 | |
スプライン補間を行うことで、ルンゲ現象を起こさずに全ての点を通る関数を用意することができます.このスプライン補間において関数に影響するものは特定の区間のところのみになり関数全体の影響は受けません。 | スプライン補間概要 |
スプライン関数は、
・値が連続になること
・次の関数との接続点で値が与えられたyと等しくなること
・次の関数との接続点で傾きが連続すること
・次の関数との接続点で二次微分が連続すること
を守るものとされます. | スプライン関数の定義 |
スプライン関数を求めるときには、S(x) = a + b*x+ c*x^2 + d*x^3のような3次スプライン関数を作成し、このパラメータを求めていきます.
これらは上記の定義と合わせれば連立方程式から導くことができます. | スプライン関数を求めるには |
 | スプライン関数(Wikipediaより) |
3.パラメータの次元がサンプル数と等しい補間 | |
多項式補間などにおいてはパラメータの数は使用する特徴量の次元数によって決まります.しかし、特徴量を増やしすぎた場合はとんでもなく計算に時間がかかってしまいます。
そこでカーネル法を用いて補間の関数近似を行うと、サンプリングした数がパラメータの次元になり、計算自体も簡単になります.
カーネル法は上記の多項式補間と少し異なり、以下の関数ようにカーネル関数を決めてそれを決めた上でαを決めていくことになります.下の式のように全点の値を使用して関数が定義されており、全点を通った関数が出力されます. | カーネル法概要 |
$$f(x)=∑_{n=1}^N \alpha_nK(x,x_n)$$
$$K(x,y)=∑_{m=1}^Mϕ_m(x)ϕ_m(y)$$ | α_nは係数
xが入力ベクトルでx_nが与えた制御点.
少なくとも与えられたxでf(x)は与えられたyと一致します.
下側がカーネル法の定義です. |
通常,過学習を防ぐために正則化項を最終的な解の式に加えます.これを加えることで過学習を防ぎ自然な関数にします.
しかし、それを加えると今回の「全点を通って」というのが守られないので、ここでは記述していません. | カーネル法の正則化について |
この章を学んで新たに学べる
Comments