-
 @ThothChildren
@ThothChildren
- 2018.5.15
- PV 511
全点通る滑らかでない関数近似をしたい
ー 概要 ー
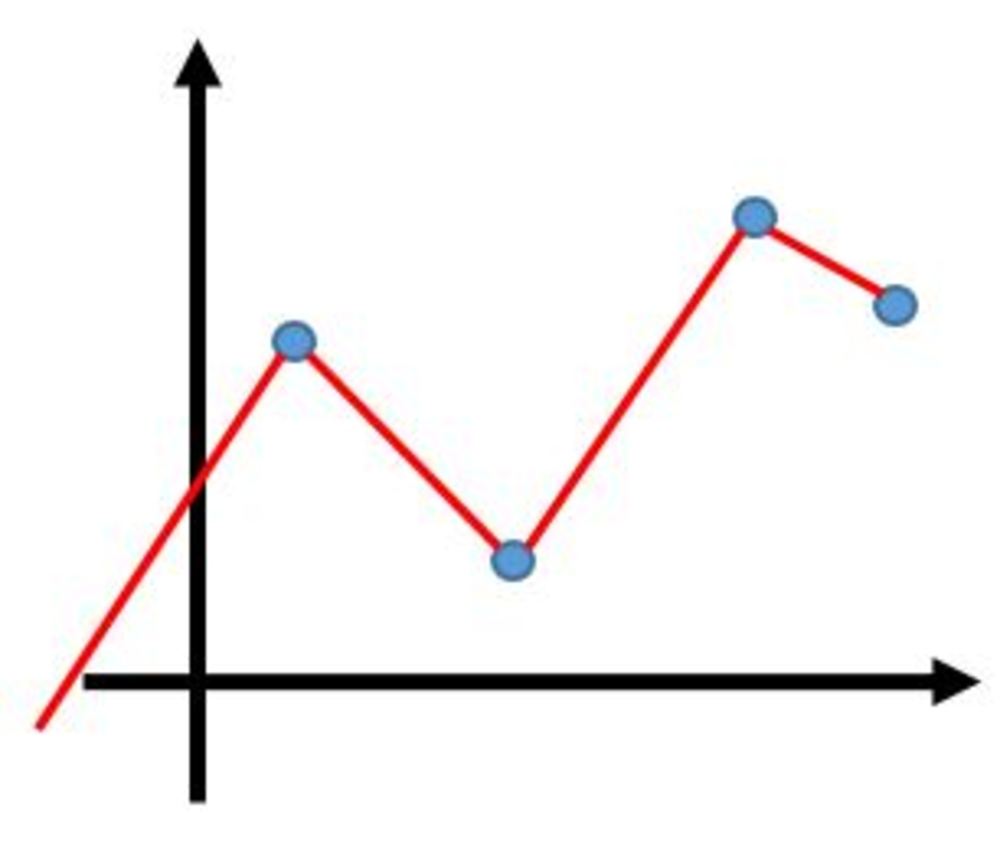
データの全点を通るが滑らかでない関数でもかまわない関数近似をする方法についてです。ここでは折れ線近似のみの紹介になります。
この章を学ぶ前に必要な知識
条件
- 複数のデータ点を用意
効果
- 点以外の部分の補間が用意に可能
- 全点を通る関数を得る
ポイント
- 各点において傾きが不連続
- 計算量がO(n)
解 説
全点を通って滑らかでない関数の近似をする方法は、折れ線近似のみになります。
折れ線近似は、すべての点を使いながら関数の補間をします.\(x_t\)から\(x_{t+1}\)までの間を線形の\(y=ax+b\)の形で補完することを繰り返し.間の数だけ補間の関数を用意して補間を行います.
| 全点の点群を通る滑らかでない関数を作る |
折れ線近似では各データ間でおのおのの補間曲線を考慮するため、
以下の特徴が挙げられます。
・データにノイズがあるときに周辺データを参照していないため外乱に弱く、誤った関数を推定しまいうる.
・各データ点で傾きが不連続になっているため、扱いにくい.
・関数の表記が区間ごとになってしまう. | 折れ線近似の特徴 |
この章を学んで新たに学べる
Comments


