-
 @ThothChildren
@ThothChildren
- 2022.10.9
- PV 344
高速フーリエ変換FFT
ー 概要 ー
高速フーリエ変換(FFT, Fast Fourier Transform)は与えられた時系列データから離散フーリエ変換を高速に処理する方法です. N個の離散的な時系列データからN個の離散的な周波数データへ変換します.
この章を学ぶ前に必要な知識
条件
- 入力も出力も離散的なデータ
- データの入力数Nは2の累乗であること
効果
- 離散フーリエ変換のO(N^2)をO(NlogN)に低減
ポイント
- 回転因子の性質をもとに計算すべき回数を減らす
- 計算量はNlog2(N)
解 説
高速フーリエ変換の図解したわかりやすい解説.
【数分解説|眺めて理解】高速フーリエ変換 FFT: 離散フーリエ変換を回転因子の特性を活かしてコンピュータでの計算を高速にし計算量をNlogNにする手法.【高速フーリエ変換4/4】
| |
1.回転因子の特性 | |
高速フーリエ変換と離散フーリエ変換を使った処理では、行列演算を行うことになります. 指数表現だと把握しにくいため、ここで
$$W_N^{t}=e^{2\pi i \frac{t}{N}}$$
で表現します. これを回転因子と呼びます.
$$W_N^{N}=1$$
$$W_N^{\frac{N}{2}}=e^{\pi i}=-1$$
となります.
| 回転因子の導入 |
離散フーリエ変換、高速フーリエ変換は、回転因子を使って行列を表現しています.
この回転因子で表現することで計算の省略の仕方を工夫することができます.
使うのは大体3つあります.
・周期性 : tがN増えると一周して同じ回転を表現する
・対称性 : tがN/2増えると半周して-1かけた値になる
・tが偶数しか取らずNが偶数の時なら、t/2とN/2の回転因子に等しい
上記を使って計算を簡単にするため覚えておいてください. | 回転因子の特性 |
2.高速フーリエ変換の処理 | |
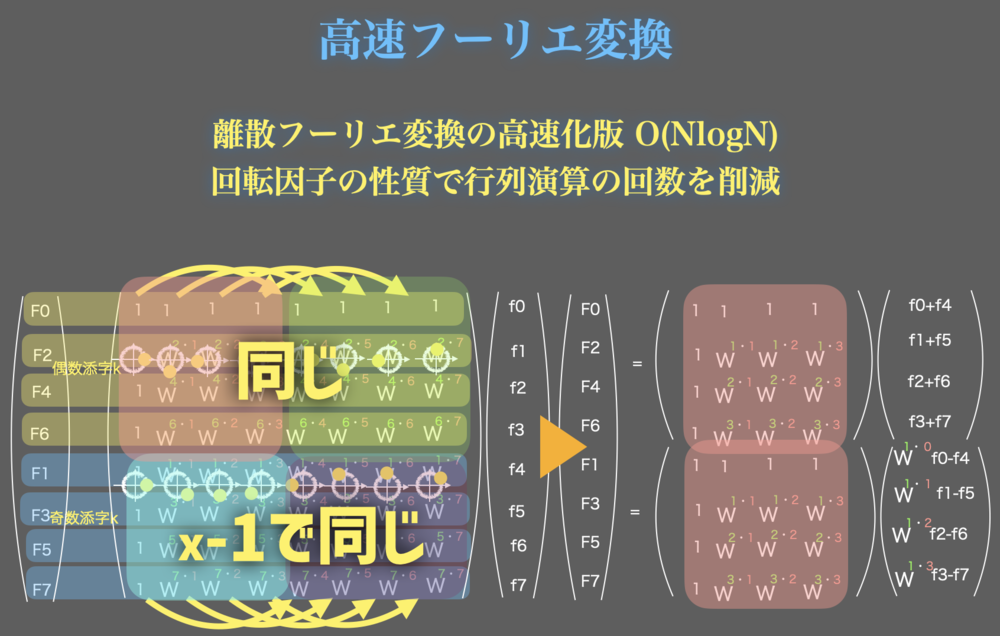
それでは、N=8の時の高速フーリエ変換をみていきます.
まずこの行列の偶数行目と奇数行目を入れ替えて上半分に偶数行列と下半分に奇数行列を持ってきます. この時小文字fの順番は変わらず、あくまで周波数の大文字Fがわの順番が変わることに注意してください. | N=8の時の高速フーリエ変換 |
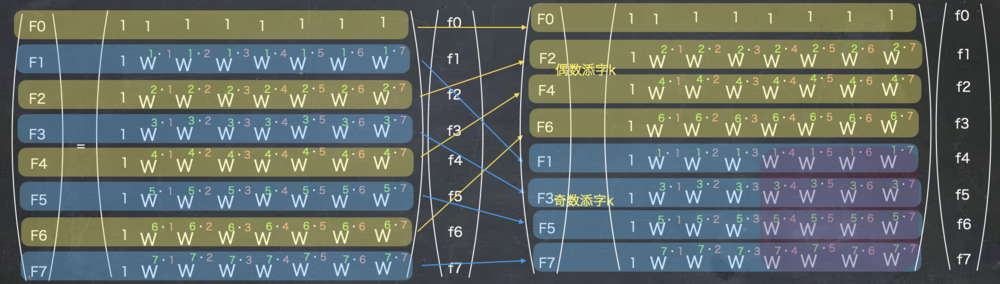 | |
上記のように分けたことで、偶数と奇数をそれぞれでまとめて扱えるようになりました.以後、上側偶数の計算、下側の奇数計算はお互いに影響しないため、それぞれで考えます.
以下のようにある行での回転因子の回転の仕方に注目してみました.
すると偶数の場合はNの半分ずらした位置で同じ回転因子になっていることがわかります. 一方で奇数の場合は半分ずらした位置では半周ずれているため、同じ回転因子になっていません.
Nの半分ずれているということは先ほどの対称性があるはずで、-1の大きさになるはずです.
偶数行番目では、kの値が偶数になり、またN/2をずらしているため、二つ合わせて必ずN倍の値の差分が出るため、一周したことに等しくなるためです.
奇数行番目ではkが奇数のため、N/2の倍数にしかなりません. そのためずらしたところでは対称性の-1倍した値になります.
| 偶数行目と奇数行目 |
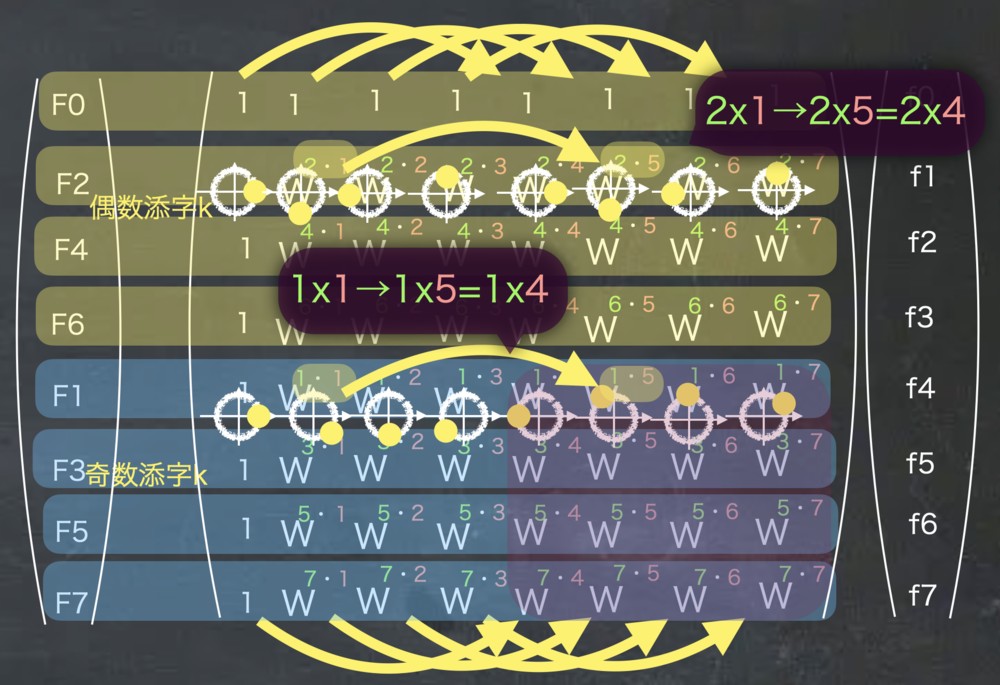 | 偶数行目と奇数行目での回転因子の状態の違い |
左半分側の全部の要素で右にN/2ずらした要素は、
・偶数行目では1倍
・奇数行目では-1倍
となるため、以下のようになります. | 行列をまとめる |
 | 偶数、奇数それぞれの右側の行列と左側の行列の関係 |
2.1.偶数行目の行列の計算 | |
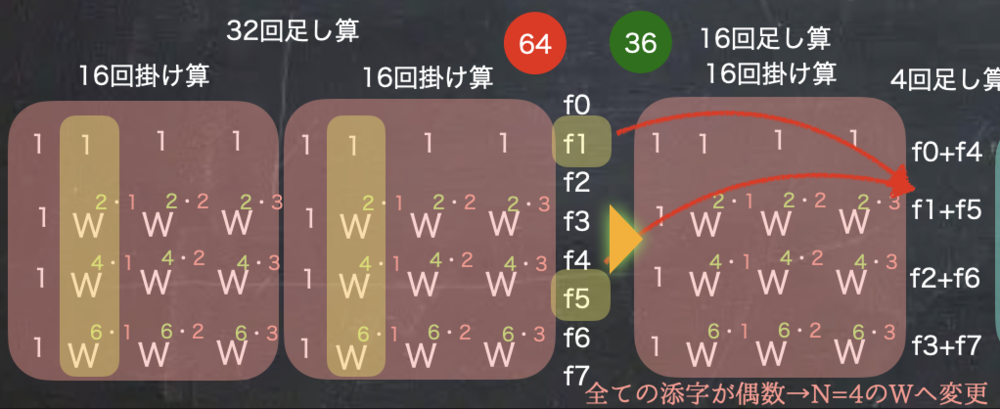 | 偶数行目の計算を削減 |
偶数行列目だけに注目してみると、係数が全く同じため、先に掛け合わせる方を足しても構いません. これによって掛け算2回してから足し算する処理が、足し算をして掛け算の処理となり、一回分掛け算が減っています.
これは行列の計算全体で数えても減っていることがわかります. | 計算の工夫 |
 | 係数を整理 |
高速フーリエ変換ではさらに4x4の行列の大きさで計算をしたいのですが、係数が8x8のようにkが増えていません. そこで、kとNの大きさを変えることで、係数を整理します. 上記のように元々全て2の倍数だったkでN=8だったのをkを2で割った値とN=4にすることで、8x8の時のような係数になりました. | 約分のような係数の整理 |
2.2.奇数行目の行列の計算 | |
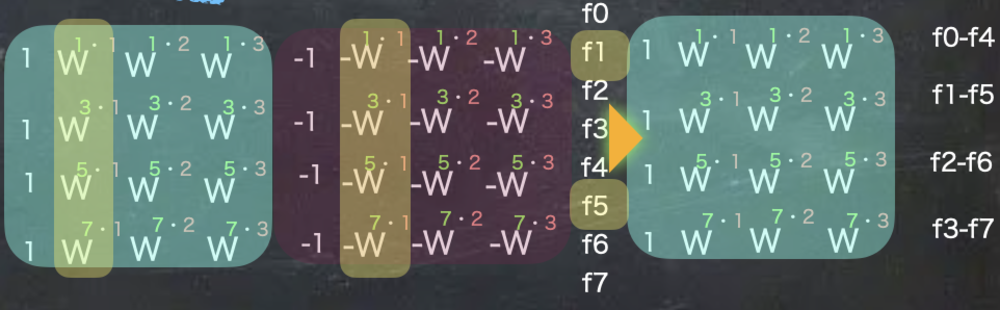 | 奇数行列も同様のまとめ方ができます
|
奇数行列目でも偶数行列と同様にまとめることができます.
ただし-1を掛け合わせているので、今回は足し算ではなく引き算になることに注意してください.
これで行列を共通化できましたが、偶数行列の行列とは係数が異なってしまっています.
これを同じにして4x4でも同様の計算を行えるようにことで今後の計算も高速化できます. | 奇数行列の計算の工夫 |
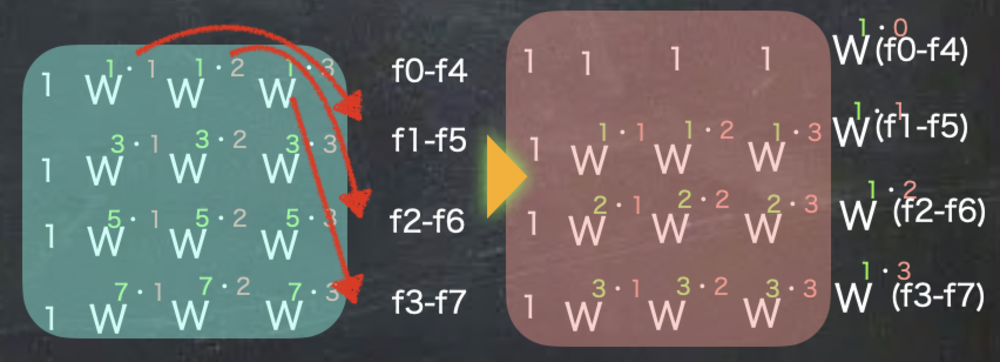 | 1行目をすべて1にするように引き算した項目にWを予め掛けてしまう. |
上の画像のように、1行目を8x8のように全て1にするため、既にかかっているWを先回りして引き算している項目に掛けてしまいます. 各要素を逆にWに割ります.
また、偶数行と同じように各添字を半分にしてNも半分にすると偶数行列と全く同じ係数の行列が得られました. | 奇数行列の計算の整理 |
2.3.N=4への分解 | |
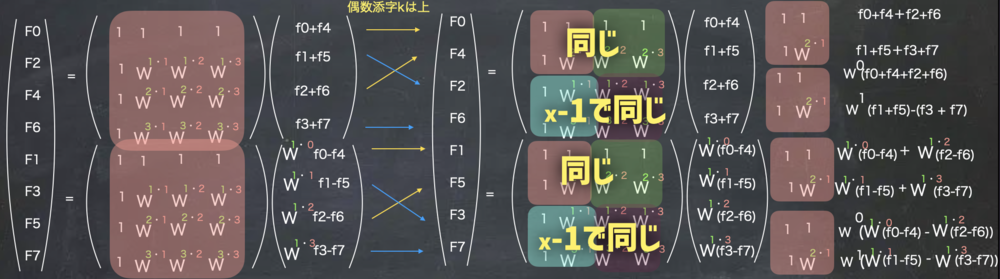 | 4x4での処理 |
これまでの処理によって、8x8の行列は上図左側のように整理されました
もはや上側の処理と下側の処理は完全に分かれたので、
それぞれで8x8の分解のようにさらに2x2の行列の分解していきます.
各項目を足したり、引いて回転させたりといった処理を行います. | N=4での処理. |
2.4.N=2の処理 | |
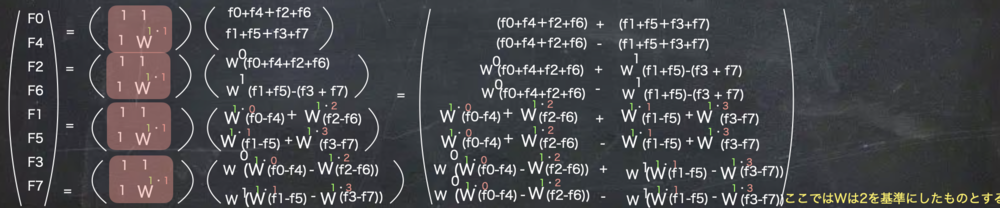 | N=2の処理 |
最後はN=2の大きさの処理ですが、ここまでくると既に分解のしようがないので、
そのまま足し算と引き算をするだけで良いです.
そうすると最終的に右のような計算列を得られます.
上記の式を見ると同じような計算が何度か現れているのがわかります.
これを可能な限り繰り返し行わないようにするのがバタフライ演算です. | 最終的な計算 |
3.バタフライ演算 | |
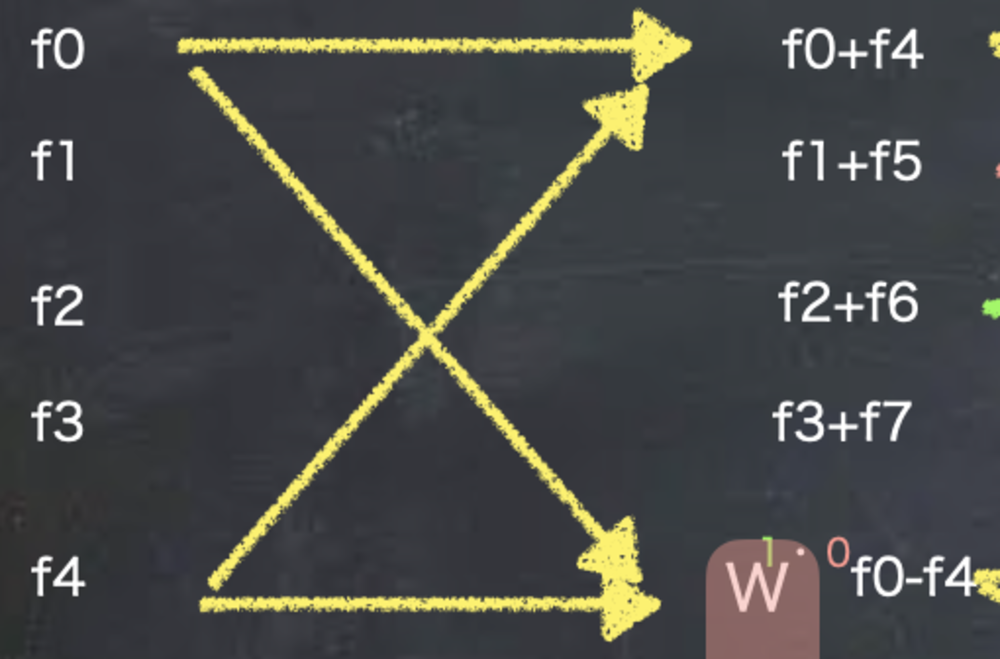 | f0とf4に注目した場合の処理.
足し算と引き算後の回転の掛け算が行われる. |
上記を繰り返すと同じ値を使い回して、それぞれの計算を効率よく行うことができます.このクロスする形が蝶のような形のため、バタフライ演算と呼びます.
| バタフライ演算 |
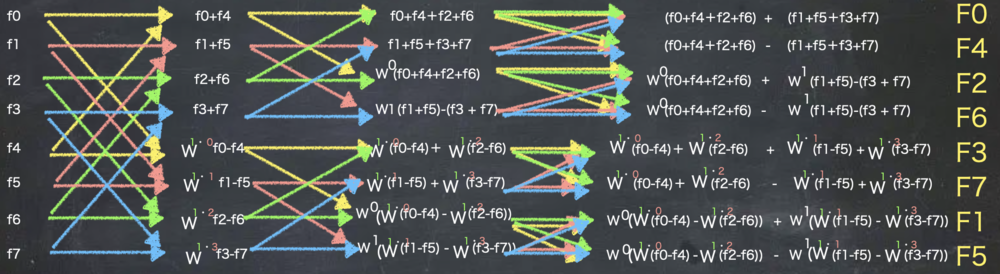 | バタフライ演算の繰り返し |
4.計算量 | |
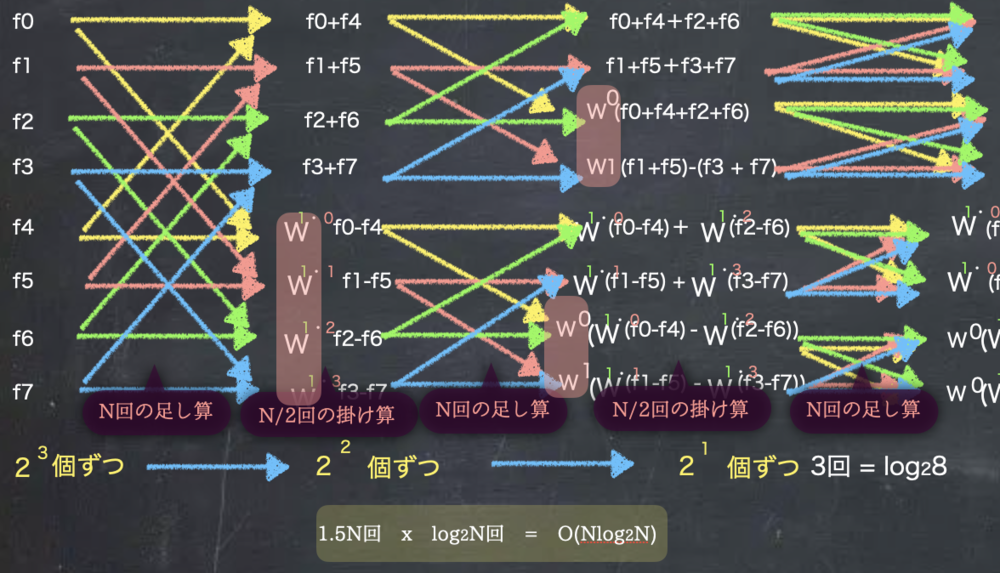 | 2の3乗が2の1乗になるまで分解され、
それぞれでN回オーダーの計算 |
Nが2のx乗とすると、上記のような段数はx回となるため、段数はO(logN)のオーダーです.
$$log_2N = log_2{2^x} = x$$
一方で一つずつの計算では、足し算と引き算の処理があるため、段数ごとにもO(N)のオーダーです.
つまり全体としては、段数xO(N)のオーダーとなるため
$$O(NlogN)$$
であることがわかります. | 計算量の求め方 |
5.ビットリバース | |
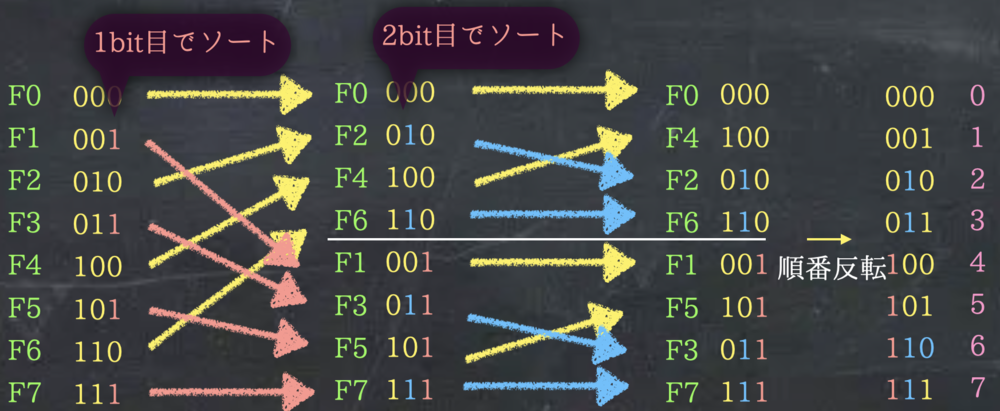 | Bit Reverse ビットリバースの処理 |
偶数行や奇数行を入れ替えているため、
大文字Fは計算結果が出てくる行が初めの行列から変わってしまっています.
そこでどこに出てくるかの位置を求めるのがbit reverse、ビットリバースの処理です.
初めにF0~F7を二進数にします.偶数と奇数で分けるのはすなわち末尾の1bitを見て並び替えていることになります. さらに次では、末尾から二つ目の1bitをみて並び替えていることになります.
これを行なっていくと、下の方には1のbitが右によっているものから並んでいきます.
このbitを110→011、001→100のようなbitの順番を逆転させると、数字になります.
ここから、2進数にしてbitの順番を逆転させて10進数に戻すとそれが出力される位置であることがわかります. F6→110→011→3行目で正しく出ています. | ビットリバース |
この章を学んで新たに学べる
Comments


