-
 @ThothChildren
@ThothChildren
- 2019.3.3
- PV 2136
パーティクルフィルタ
ー 概要 ー
パーティクルフィルタ(粒子フィルタ、モンテカルロフィルタ)は、複数の粒子にノイズをくわえながら観測データとモデルを元に内部状態を推定しく手法.非線形なモデルに対しても適用でき、粒子の数だけ精度はよくなるが、計算量もその分増える.実装が簡単で様々な分野で適用することができるのが特徴.
この章を学ぶ前に必要な知識
条件
- 一番それらしいという評価ができる尤度関数を設計しておく
- 粒子の数をあらかじめ決めておく
- システムモデル(x_t-1からx_tを予測する関数)を用意しておく
効果
- 逐次的に内部状態を推定することができる
- センサをもとに現在の位置情報を推定できる
- 点群や画像で物体を追跡できる
- 非線形なモデルでも推定可能
ポイント
- 時間計算量は粒子数をnとしたときO(n)
- 実装が容易
- リサンプリング→予測→観測→尤度計算の繰り返し
解 説
わかりやすいパーティクルフィルタの解説 | |
パーティクルフィルタ(Particle Filter, 粒子フィルタ、モンテカルロフィルタ)は、複数の粒子にノイズをくわえながら観測データとモデルを元に内部状態を推定しく手法.非線形なモデルに対しても適用でき、粒子の数だけ精度はよくなるが、計算量もその分増え、粒子数がNのときに時間計算量はO(N)となる.
実装が簡単で様々な分野で適用することができるのが特徴.
パーティクルフィルタでは、任意の分布を粒子の分布の密度で近似できるため、
非線形のモデルにも適用できている.
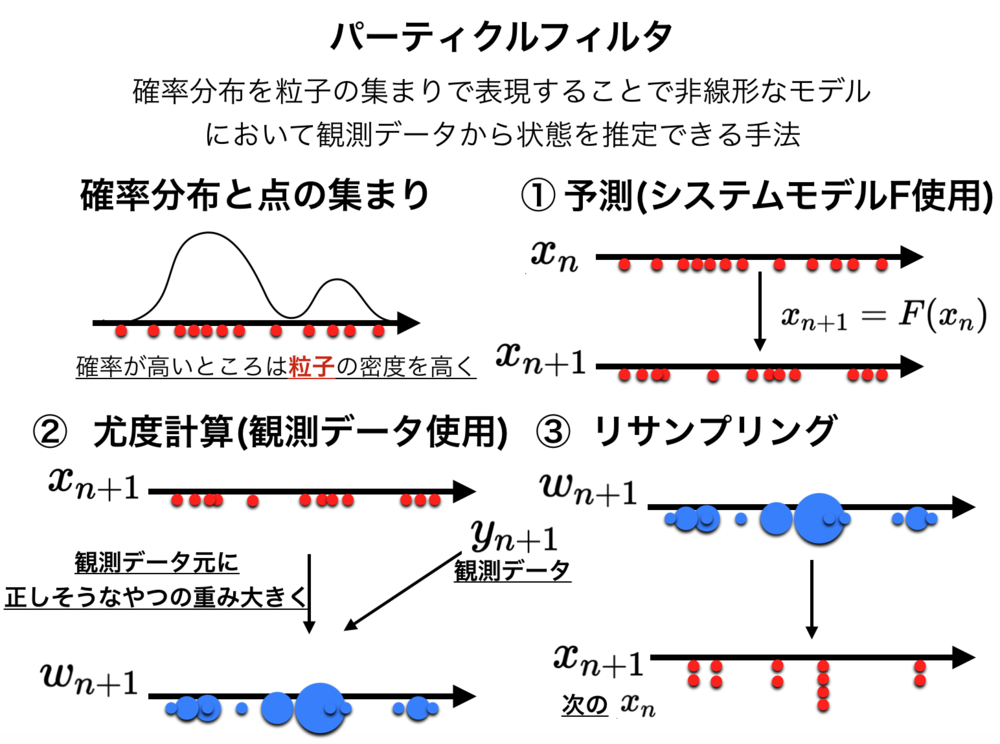
以下の絵がパーティクルフィルタの処理の流れの概要です. | パーティクルフィルタとは |
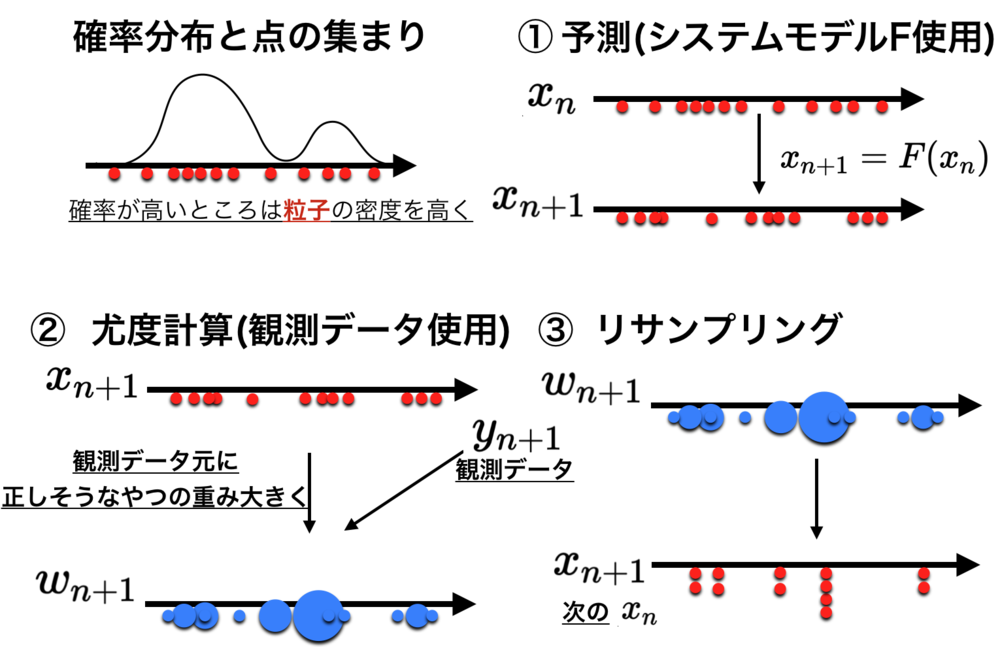 | パーティクルフィルタの処理の流れ
①→②→③→①→②→...
と逐次的に処理をしていく.
あらかじめ必要な関数は、
①の予測するためのシステムモデルの関数
と
②の観測データと各粒子からそれぞれの尤もらしさを計算し、正規化した重みを算出するための尤度関数
になります.
リサンプリングした状態では重みの多いところで同じ値が多いので、①の予測時にノイズを加えます. |
上図のワンセットを繰り返していくことで、モデルの状態を推定し続けます.
この場合推定しているのはもちろん\(x_n\)です.
左上に描いているように確率分布で確率が高いところにはたくさんの粒子をばら撒くことでその粒子の偏り方(濃度)で分布を近似しています.
変数
\(x_n\)が状態(未知, 求めたい)
\(y_n\)が観測されるデータ(既知)
\(w_n\)が重み(尤度を元に全粒子の尤度で正規化したもの)
を扱い、あらかじめ決めておいた関数
関数
\(F(x)\) : 次の\(x_n\)を予測するためのシステムモデル関数(ここでノイズも付与)
\(H(x,y)\) : 予測した\(x_n\)と観測した\(y_n\)を元に観測したデータから考えて尤もらしいと考えられるものに高い尤度を与える尤度関数(上図では\(H(x,y)\)は書いていません.)
でモデルを推定行きます.
それでは各段階についてです.
①予測
初期化したばかりの場合は、均一に粒子を撒きます.
今回の図の状態はすでに何度か推定を行なっていて、リサンプリングした後の状態です.
リサンプリングによって得られた\(x_{n}\)を元にまず予測をします.
予測は\(x_n\)と\(F(x)\)を元に\(x_{n+1}\)を計算します.この過程でノイズも入れます.
$$x_{n+1} = F(x_n, noise)$$
②尤度計算
今回予測したデータ\(x_{n+1}\)と観測したデータ\(y_{n+1}\)を使って\(H(x, y)\)から尤度計算を行います.観測したデータが与えられたときにそれぞれの予測データはどれくらいありえるのかを計算します.
その値を元に全体で正規化しつつ重みを計算します.
$$w_{n+1} = H(x_{n+1}, y_{n+1})$$
重み正規化
$$w_{n+1} = \frac{w_{n+1}^{(i)} }{\sum_{i}^p w_{n+1}^{(i)}} $$
③リサンプリング
②で得られた重みに応じてパーティクルの移動を行います.
重みが小さいものを削除して、重みが多いところにその重みに応じたパーティクルが配分されるようにします.このとき同じ値になるパーティクルができますが、①のときにノイズを付与するので気にする必要はありません. | パーティクルフィルタ詳細. |
それぞれの段階では多数のパーティクルが自身の値を持っているだけで、
「結局どこにいると思うの?」という推定値が提示されていません.
そこで複数の方法がありますが、一つの方法として
「重みつき平均値」を取る方法が採用されることがあります.
$$\bar{x} = \sum_{i=0}^p w_{n+1}^{(i)} x_{n+1}^{(i)} $$
単純に重みに応じて各パーティクルの値を平均するという手法です.他にMAPで行う場合もあります. | 状態推定で推定値を計算 |
パーティクルフィルタの二次元マップ状での様子.
赤い点がそれぞれの粒子です.集まっているところほど確率が高いということになります.
観測する時間が長くなるほど、間違いが減っていっているのがわかります. | |
別の例です.
歩きながら分岐しては間違っているものは消えていくというのを繰り返しているのがわかります. | |
こちらはKinectから得られる3次元点群データを使った場合の点群トラッキングです.
赤い点がパーティクルとして表示されています. |
この章を学んで新たに学べる
Comments


