グレンジャー因果検定

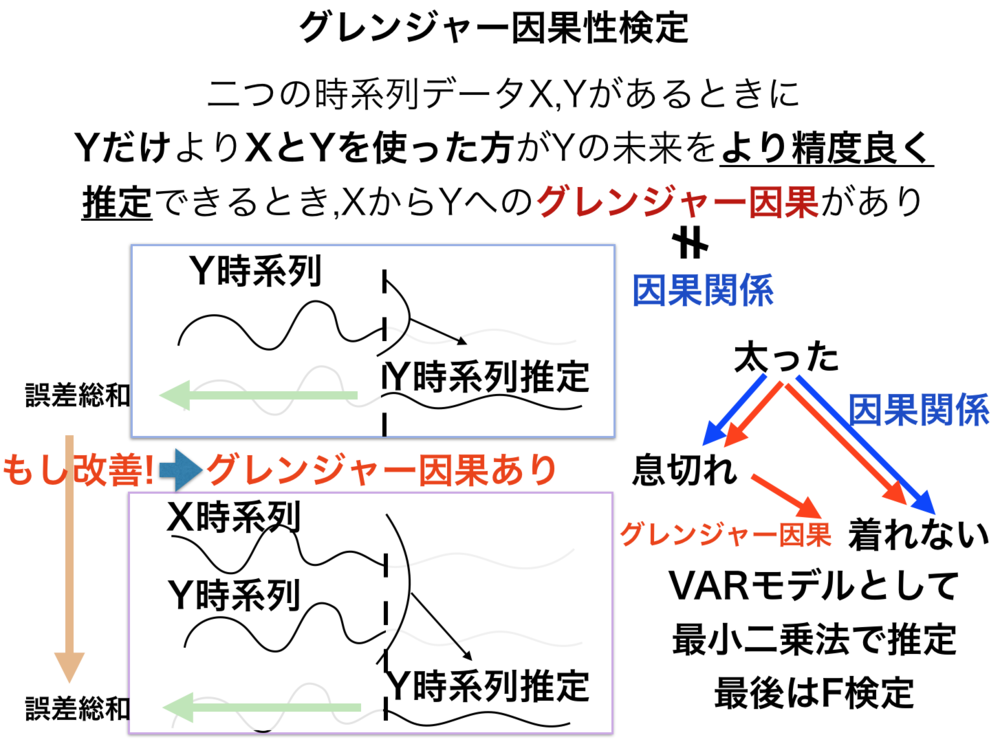
グレンジャー因果検定はある二つの時系列データが与えられたときにその時系列間にグレンジャー因果性があるかどうかを判定する検定. グレンジャー因果は本当の因果関係ではなくあくまで片方のデータ列を使うことでもう片方のデータ列単体でそのデータ列の未来を推定するよりもっと良く推定できる関係.例えば、「太った」ことで時間差で「息切れやすく」なり、さらに時間差で次第に(「太った」が原因で)「昔着れた服が着れなくなった」という事実があったとすると、「体重の時系列」と「息切れ時間の時系列」から将来の「息切れ時間の時系列」を精度よく推定できると考えられるのでここにはグレンジャー因果があると言える. 「息切れやすくなった」と「昔着れた服が着れなくなった」は因果関係はない(どちらも「太った」が原因)がグレンジャー因果性があり、「太った」と「息切れやすくなった」は因果関係もグレンジャー因果性もある. 因果関係があるものには必ずグレンジャー因果性があるが、グレンジャー因果性があっても因果関係があるとは限らない. どのようにグレンジャー因果性があるかを測るか 上記のようにグレンジャー因果性は、二つの時系列が与えられた時にもう一つの時系列の未来を推定するのに役に立つかどうかを計測しようとしています. 結果から言えば、具体的には以下のようにグレンジャー因果性を計測します. 二つの時系列XとYがあるときに、「Yの未来をYだけで推測したときの間違いの大きさ」に対してXも考慮した「Yの未来をXとYを使って推測したときの間違いの大きさ」が有意に小さくなれば、XからYへのグレンジャー因果性が存在するとする.

二つの$x, y$の時系列データがあるとして$x$から$y$へのグレンジャー因果性があるかどうかを検定する.(また、多変量でも構わないがここでは一変量とする) 時系列は定常を想定するが、そうでない場合はなんらかの変換をしておく. 1. まず、$y$単体でVARモデルの推定を行い、データと予測値の残差平方和$SSR_y$を計算する. 過去$(t -1)$~ $(t-p)$の$p$ 個分の$y$のデータを使って$y_t$を最小二乗法(OLS)で推定する. $$y_t = a_0 + a_1 y_{t-1 } + \cdots + a_p y_{t-p } + error$$ 上記で推定されたモデルを使って、残差平方和$SSR_y$を計算 2. 次に、$x,y$の両方を使ってyのVARモデルの推定を行い、データと予測値の残差平方和$SSR_{xy}$を計算する. 過去$(t -1)$~ $(t-p)$の$p$ 個分の$x, y$のデータを使って$y_t$を推定する $$y_t = a_0 + a_1 y_{t-1 } + \cdots + a_p y_{t-p } + b_1 x_{t-1 } + \cdots + b_p x_{t-p } + error$$ 上記で推定されたモデルを使って、残差平方和$SSR_{xy}$を計算 3. F統計量を$SSR_y, SSR_{xy}$から算出し、F検定 $$F = \frac{SSR_{y} - SSR_{xy}}{SSR_{xy}/(T-(2p+1)) }$$ Tは全データ量.