-
 @ThothChildren
@ThothChildren
- 2019.2.7
- PV 355
Burrows–Wheeler変換
ー 概要 ー
Burrows–Wheeler変換(ブロックソート圧縮)は、情報を一切失うことなく文字列の順番を変えることで後工程で圧縮を行いやすくするデータ圧縮の前処理.繰り返し表現が増えたりするため、MTF変換や連長圧縮などと組み合わせてさらに圧縮しやすくします.もちろん可逆圧縮の処理になります.
この章を学ぶ前に必要な知識
条件
- データ圧縮の前処理として行う
効果
- データ圧縮を行いやすい文字列になる
- 一切情報量は落ちない
- 終端記号を用いればデータ量も増えない.もし終端がない場合は元の場所を示す番号の保持が必要
ポイント
- このあとにMove-To-Front変換や連長圧縮を繋げて行うことが多い
解 説
Burrows–Wheeler変換(ブロックソート圧縮)は、情報を一切失うことなく文字列の順番を変えることで後工程で圧縮を行いやすくするデータ圧縮の前処理.繰り返し表現が増えたりするため、MTF変換や連長圧縮などと組み合わせてさらに圧縮しやすくします.もちろん可逆圧縮の処理になります.
適切に実装すれば線形時間で動くアルゴリズムとなります.
また終端文字列を持つような入力文字列の圧縮であれば、元のデータから何もデータを増やさずに圧縮しやすい文字列への変換が可能です.
通常の符号化(変換)のアルゴリズムは単純ですが、復号化(逆変換)はややこしいかもしれません. | Burrows–Wheeler変換(ブロックソート圧縮)とは |
 | ブロックソートの概要図.
変換は容易ですが、
逆変換は少し手間な処理になります. |
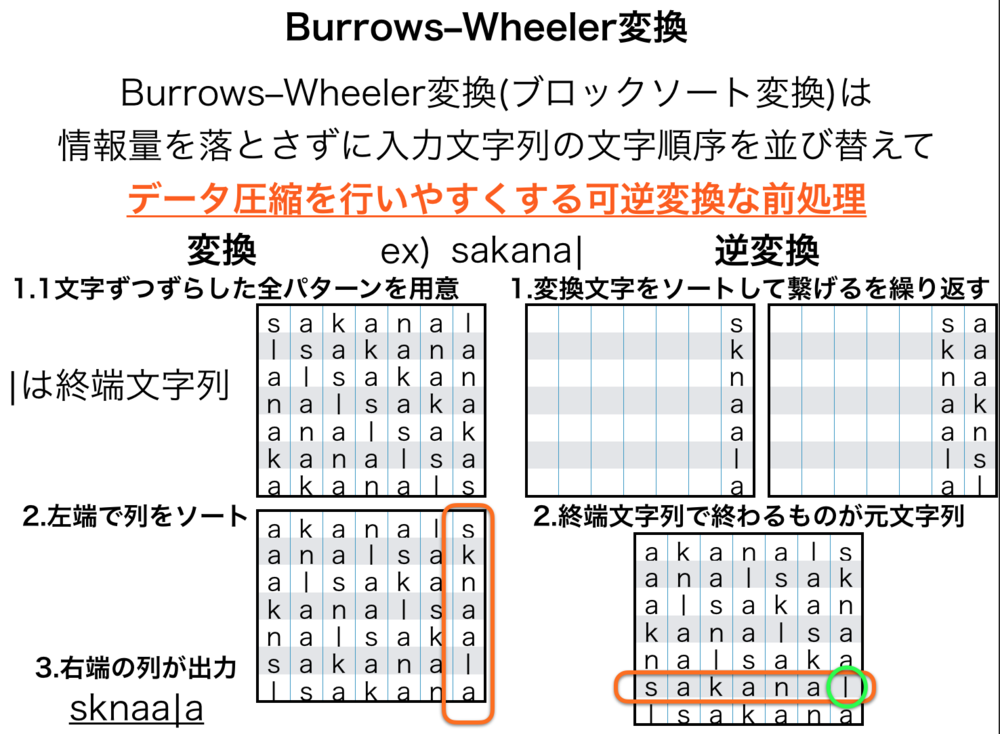
Burrows–Wheeler変換の変換時の処理.
上図の左側の処理を行うときについてです.
手順
1. まず、入力文字列を順繰りに一文字ずつずらした文字列を作り表にします.
今回入力文字列を"sakana|"(|は終端記号)とした場合は、それを一文字ずらした"|sakana"が次の行のデータになります.その次は"a|sakan"というように表を完成させていきます.
2. 次に一番左の行の値を元に各列を並び替えます.
今回の場合は、"s|anaka"を元にこの辞書式ソートに合わせて他の列も一緒にソートします.
3. 左端の行を取り出す
今回の場合はオレンジ色で囲まれた"sknaa|a"が変換後の文字列になります.
どの行も同じ文字列の文字を使って構成されており、今回の出力文字もsakana|に並び替えることができます.また出力文字を辞書式ソートをすれば、当然左端の行と同じ文字列も得られます.
逆変換ではこれを利用します. | Burrows–Wheeler変換 |
今度は与えられた変換後の文字列"sknaa|a"を使って元の"sakana|"を導く作業になります.
上で書いたようにポイントは、"sknaa|a"を辞書式ソートをすれば"aaakns|"が得られそれは隣接する列でありまた左端の列であるということです.
文字を一文字ずらすことで表を作ったので右端の行の文字列と左端の行の文字列は繋がるはずです.
それでは手順です
逆変換の手順
1. 出力文字列(ex. sknaa|a)を右端の行として入力します.
2. 現状の行の中で左端の行を元にソートします.
3. 左端の行の左に新しく出力文字列(ex. sknaa|a)を挿入します.
4. 2と3を繰り返して表が完成するまで繰り返します.
以上で表が完成します.この時、右端の文字が終端文字で終わっているものが正しい文字列になります.
もし終端文字を使わない場合は、変換時に表の上から何番目のデータを記録しておく必要があります.そうするとデータが増えてしまうことになります. | Burrows–Wheeler変換の逆変換 |
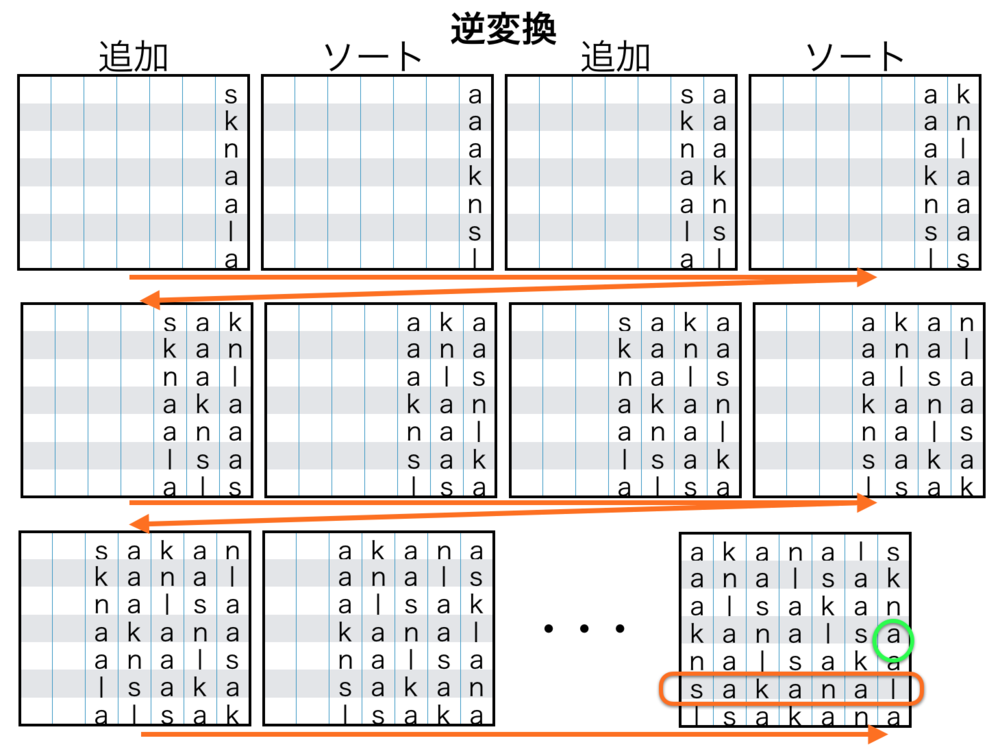 | 逆変換の処理順序 |
Burrows–Wheeler変換によってなぜ文字列が繰り返されるようになるのかについて簡単に触れる.
同じようなフレーズが複数含まれた長い入力文字列に与えられた場合、例えばそれが英語の"the"が複数含まれているときを考えるとする.上記の変換処理を行うと"he"で始める列が多数含まれてそれらがソートされたときに"he"で始まる列が左端に連続すると同時に、対応する列の右端においても"t"で終わる部分が連続することとなる.これを出力文字列とした場合に、その文字列の中にtが連続することとなる.
つまり、頻出フレーズがある場合それらはソートによって左端にも右端にも集められるため同じ文字列が連続することになる.
そのため、フレーズが頻出するようにするためには繰り返しフレーズの登場しやすい入力文字列は長くなっている方が好ましい. | Burrows–Wheeler変換でなぜ圧縮しやすく文字が繰り返しやすくなるのか |
この章を学んで新たに学べる
Comments


