算術符号は、与えられたデータを0~1の有理数に割り当てることで符号化する.頻度に応じて有理数のとれる幅を変更することで、頻出するものほど短い表現を、滅多に現れないものほど長い表現になるようにできている.テキスト圧縮や画像圧縮において用いられている.
以下に具体的な処理を示す. | 算術符号とは |
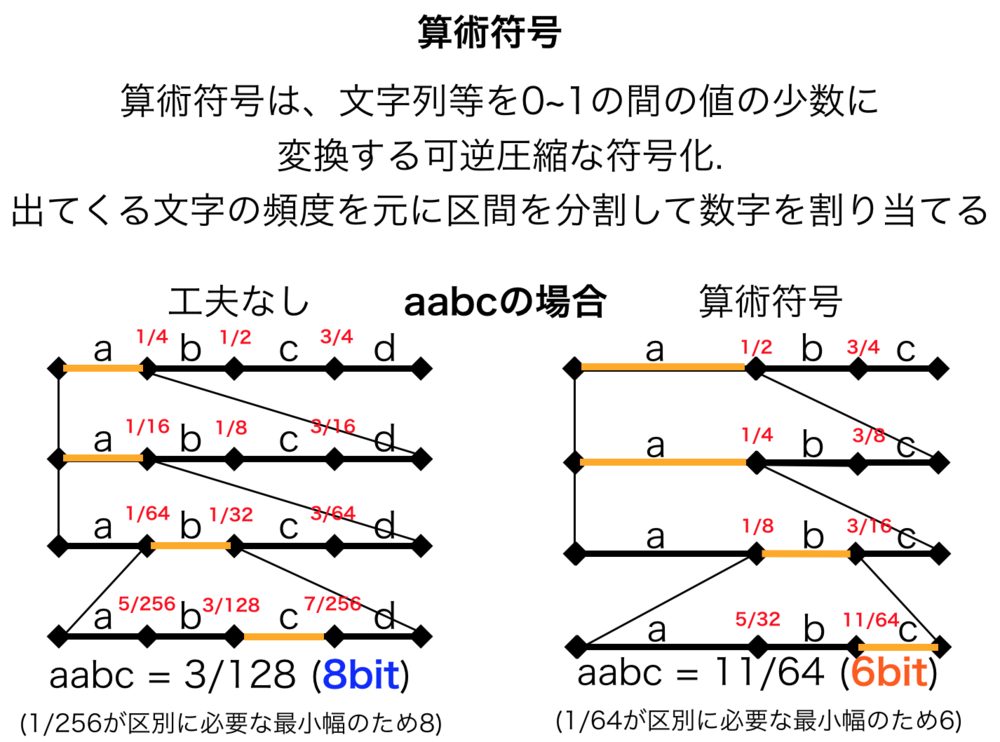
| aabcの文字列を算術符号化した場合の図
左側は特に工夫なく行なっている場合.
単純な符号化をしているだけで、常に8bitに全ての語句を変換している.
一方で、右側の算術符号においては、出現が0であるdには一切符号をつけず、頻度の少ないものにも符号を減らすことでより効率的な符号化を可能にしている. |
算術符号の符号化は上の図のように行う.
算術符号化手順
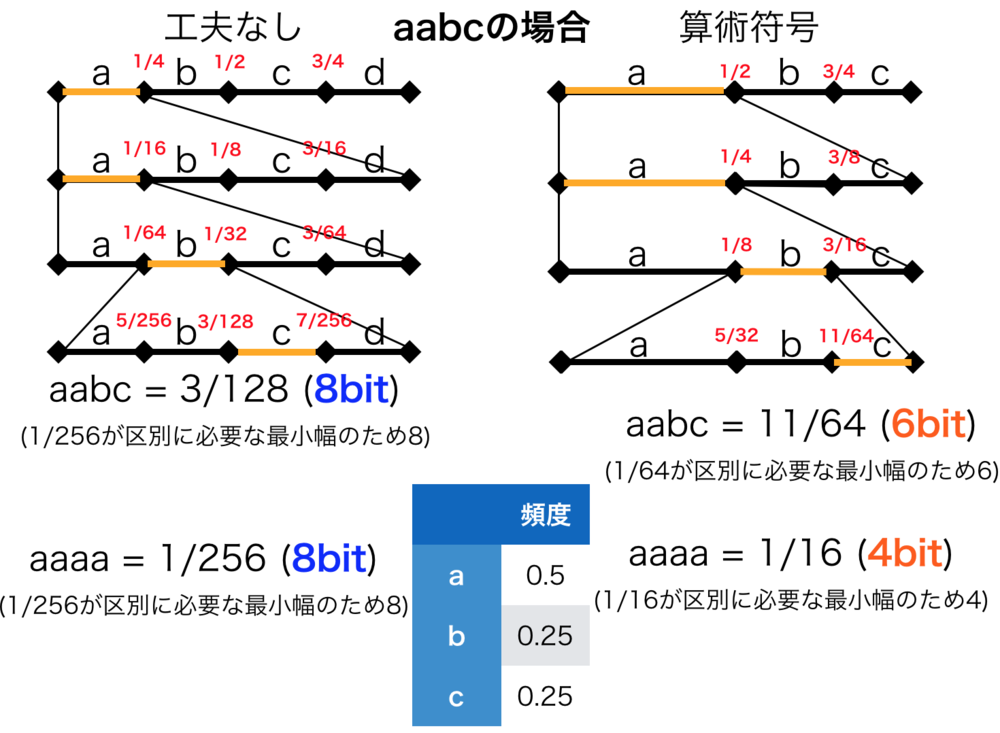
1. まず事前に各文字の頻度を求めておく.(今回はa:0.5, b:0.25, c:0.25としている)
2. 1.で求めた頻度を元に数直線上に各頻度の大きさに合うように区間を引く
3. 与えられた文字列(aabc等)の先頭の文字から一つずつ文字を選択して、区間を選択しては、その区間を再度頻度に応じて区分することを繰り返す.
(今回の例ではaを選択した後は、aa,ab,acの区間からaaを選択し、その後aaa,aab,aacから区間aabを選択する)
4. 文字列分選択を終えたら、その区間の最大値と最小値を得て、対応する符号化を行う.
4.において「区間の最大と最小を2で割った値を対応する符号」とする場合や「最小の値を対応する符号」とする場合がある.
最小の値を対応する符号とすると今回の場合は"aabc" = "11/64"となります.
区間の幅の逆数に対して\(log_2\) をとったものが精度に必要なbit数になります.
今回"aabc"であった場合は、幅が\(\frac{3}{16} -\frac{11}{64} = \frac{1}{64} \)なので
$$log_2(\frac{1}{\frac{1}{64}}) = log_2(64) = 6(bit)$$
が必要な桁数ということになります.
この必要な桁数は符号化する語句によって異なります.
例えば上図のように"aaaa"の場合は\(\frac{1}{16} \)が幅になるため\(4bit\)になることがわかります.
このように算術符号を用いた場合は必要なbit数が入力文字列によって変動し、頻出語句ほど数直線での区間の幅が長くなり、必要bit数が減少することで、全体として短い表現を出すことができます.
| 算術符号の符号化 |
算術符号の復号化は難しくありません.
符号化と同様に頻度の表と数直線を使います.
算術符号の復号化
1. 与えられた値を元にどの区間に含まれているかを繰り返し求めていくことで復号.
以上です.
今回の例で言えば、
11/64の場合, 1/2より小さいため、一つ目はaとわかります.
また11/64は1/4よりも小さいため、二つ目はaとわかります.
次は11/64は1/8より大きく3/16より小さいためbとわかり、
同様にして最後がcとわかります.
ただひたすら区間の中でどの割合にあるかを見つけることで符号化された元の文字列を求めることができます.
しかし、一つだけ工夫が必要になります.
何も情報がない場合は、いつ復号化を止めればよいかわからず、cのあとも永遠にaaaaaaaaaとで続けてしまいます.
そこで、多くの場合二つの対策を取ることになります.
・符号化終了記号を文字列および頻度表に入れておく
・あらかじめ符号化された文字数を決めておく.
上記どちらかの対策を入れておけば、永遠にすることなく復号化することが可能です. | 算術符号の復号化(Decode) |
ハフマン符号では、各文字の頻度を求めてその一つの文字に対してそれぞれ符号化を行なっていた.そのため一文字に対して必ず1bitを使わなくてはならない.
しかし、ただ単純にaを0,bを1とするより、例えば"aaa"を0,"bbb"を1といったように語句をひとまとめに符号化した方がより効率的な圧縮ができることがある.つまり,"aaa"を0とできるならば、3文字に対して1bitを割り当てることができ、よりよい符号化となる.ところが、ハフマン符号ではそれを一般的に行うことが難しかった.
一方で算術符号においては、語句の一つ一つに符号化をすることができ、その文字の出現頻度に応じて符号長さを決めることができるようになった.これによって一文字あたりに必要なbit数を下げることを実現している. | |
 @ThothChildren
@ThothChildren