-
 @ThothChildren
@ThothChildren
- 2018.11.4
- PV 1205
ドロネーの三角形分割
ー 概要 ー
ドロネーの三角形分割は、いかなる三角形の外接円も他の点を内包しない性質を持つ分割の仕方である.どの隣接する三角形を統合してもその外周は凸包となる.また、三角形の3つの角度の最小値が最大になるような分割を行う.

この章を学ぶ前に必要な知識
条件
- 平面状にちらばった点群.それを元に三角形分割.
効果
- 点を元に領域を三角形分割することができる
- ドロネー図の三角形の中心を結ぶとボロノイ図
- 細長い三角形を防ぐ(鋭い角度を持たない三角形のみとなる)
ポイント
- ポアソン過程によってばらまかれている点では平均6つの三角形に一つの点は隣接する.
- 分割で生成された如何なる三角形の外接円も他の点を内包しない
- どの隣接する三角形を統合してもその外周は凸包となる
- 薄く潰れたような細長い三角形をSliver Triangleと呼ぶ.
解 説
ドロネーの三角形分割は、いかなる三角形の外接円も他の点を内包しない性質を持つ分割の仕方である.この図はドロネー図とも呼ぶ.
ドロネー図の三角形の特徴
・どの隣接する三角形を統合してもその外周は凸包となる.
・三角形の3つの角度の最小値が最大になるような分割を行う.(あまりに高さのない細い三角形を防ぐ)
・ポアソン過程によってばらまかれている点では平均6つの三角形に一つの点は隣接する.
・ドロネー図の三角形の中心を結ぶとボロノイ図 | ドロネーの三角形分割 |
 | ドロネー図.(Wikipediaより引用)
外接円がうっすら書かれているがどの外接円にも3点以外が含まれていない( |
ドロネー図では、二つの隣接した下のような三角形を見たときに、共通の辺に接していないαとγの角度の合計は180度より小さくなることが知られています.
このとき、辺を直行する方向に結び直すとドロネー図の三角形の条件を満たすようになります.
この操作をFlip処理と言います. | Flip処理とは |
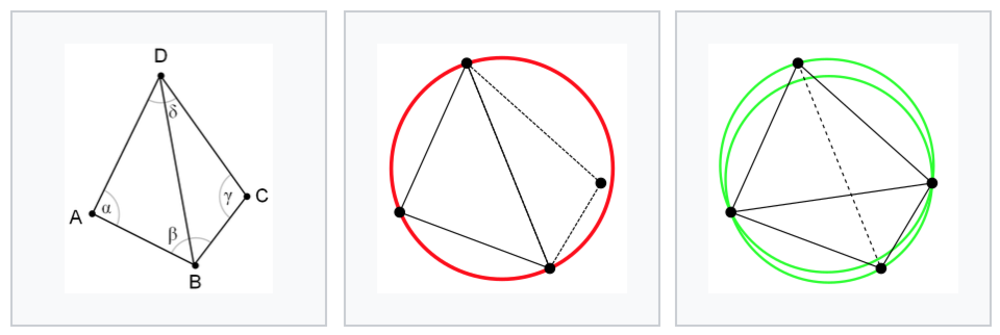 | Wikipediaより引用.
左端が最初の分割状態だったとする.αとγの合計は180度を明らかに越すため、これはドロネー図の三角形の条件を満たしていない.(中央の図でも確認できる)
そこで直交する線を引き直すことによって、新しい分割となりドロネー図を満たす図形となる. |
1.ドロネー三角形分割の各種アルゴリズム | |
1.1.Flipによるドロネー三角形分割 | |
Flipによるドロネー三角形分割は非常に単純になっています.
1. まず適当に三角形分割を行う.
2. 以下の図の要領でドロネーの三角形の条件(外接円に他の点を含まない)を守っていない三角形に対して、上記Flip処理を行う.
時間計算量としては点の数をnとして、O(n^2)となってしまいます. | Flipによるドロネー三角形分割 |
1.2.分割統治法によるドロネー三角形分割 | |
与えられた点群を二つに分割していき、二点ずつ統合していく方法による分割統治法のドロネー三角形分割.
O(n log(n))の時間計算量になり早いことが知られる. | 分割統治法によるドロネー三角形分割 |
この章を学んで新たに学べる
Comments


