-
 @ThothChildren
@ThothChildren
- 2018.11.4
- PV 667
可操作度
ー 概要 ー
可操作度は特異点を避けたいときに指標となる特異点との距離に当たるような数値を求められる.特異点において可操作度の値は0となる.ヤコビ行列Jを用いて求めることが可能.
この章を学ぶ前に必要な知識
条件
- ロボットのリンク、関節およびヤコビ行列
効果
- ヤコビ行列と特異点からの距離の指標を持つことが可能
ポイント
- ヤコビ行列を用いて可操作度を計算
解 説
可操作度は特異点を避けたいときに指標となる特異点との距離に当たるような数値を求めることができ、ヤコビ行列による逆運動学を解く上で参考になる値.
ヤコビ行列Jを用いて求め、特異点において可操作度の値は0となり、離れているほど大きな値になる.
| 可操作度とは |
ヤコビ行列による逆運動学についてはこちら | ヤコビ行列による逆運動学 |
可操作度の解説の前に可操作空間、冗長空間について整理する.
まずある現在位置\(r\)と関節角度\(\theta\)を用いて、以下の関係が成り立つ.\(J\)はヤコビ行列.
$$\dot{r} = J(\theta)\dot{\theta_1} $$
ここにおいて、上記方程式を解くことで得られる\(\dot{\theta_1}\)を使って実現可能な\(\dot{r}\)を集めたものを可操作空間と呼ぶ.すなわち今の位置から実現できる全ての\(\dot{r}\)を集めたもの.
一方で上記と異なる以下の式から\(\theta_2\)を求める
$$0= J(\theta)\dot{\theta_2} $$
こちらの式はどのような\(\theta_2\)を与えてもエンドエフェクタの速度に影響しない集まりとなる.これを冗長空間と呼ぶ.
上記二つの式を足すと、
$$\dot{r} = J(\theta)(\dot{\theta_1} +\dot{\theta_2} )$$
となり、やはり、影響がないことがわかる.
重要な性質として
$$Dim (\theta) = Dim(Kasousa) + Dim(Jyocyo) $$
| 可操作度の前の前提 |
可操作空間の次元の数が小さいほど、可操作空間が縮退して、より特異点に近い状態になる.一つの指標にはなるが、それでは離散値になるため、距離に近い概念として可操作度を導入する.
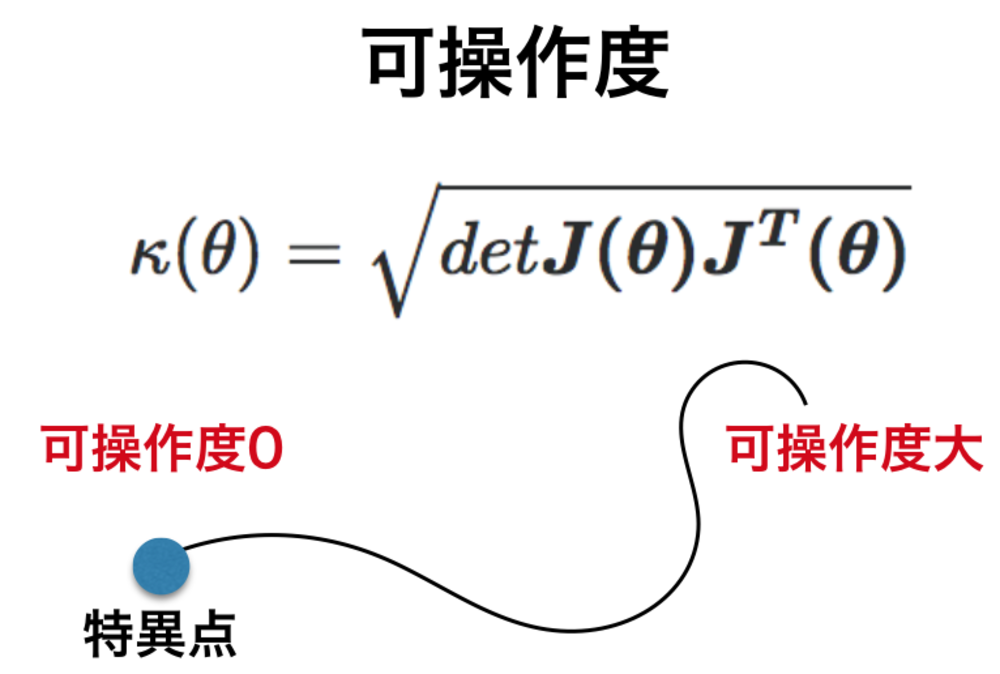
可操作度:
$$\kappa(\theta) = \sqrt{det \boldsymbol{J(\theta)J^T(\theta)}}$$
この値によって求めれば、可操作度は特異点で0それ以外で正値をとる. | 可操作度の式 |
この章を学んで新たに学べる
Comments
Reasons
知識: ヤコビ行列による逆運動学
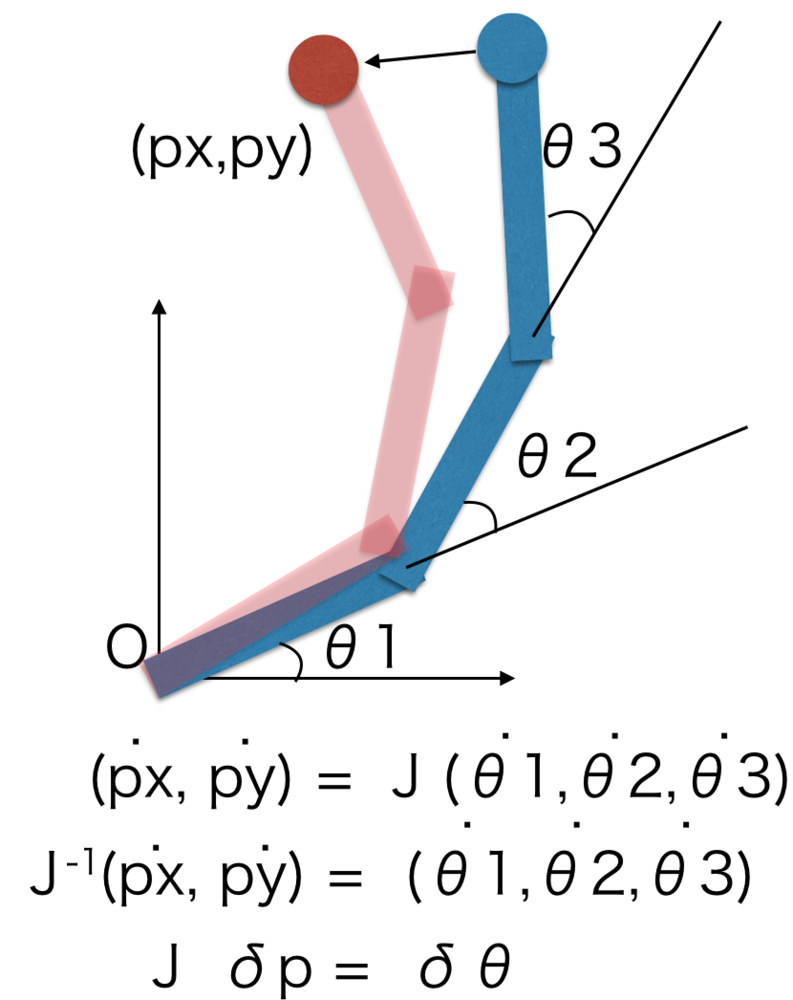
関節角度と手先位置のp=f(θ)の関係からδθ=J^-1()δp(Jはヤコビ行列)を導きこの勾配を利用して近似的に関節角を探索する方法についてまとめます.一般的に逆運動学は解析的に解けないため、このような繰り返し計算による解の導出を行います.ヤコビ行列による逆運動学はその中でも最も有名な手法です.


