球面状の距離を求めたい

球面状の二点間距離を求める方法についてまとめます.正確さを犠牲にするか計算速度を犠牲にするかで3種類の方法があります.どれも円弧距離 d = rθを利用します. ・Great-Circular Distance : シンプルに二点の間の弧度θを求めてrθで求める. ・Haversine Formula : θの計算における丸め誤差をより改善(現代の64bit浮動小数演算精度ではあまりGreatCircularと大差ない). ・Vincenty Formula : 真反対にある点同士では不正確なHarversine Formulaを改善

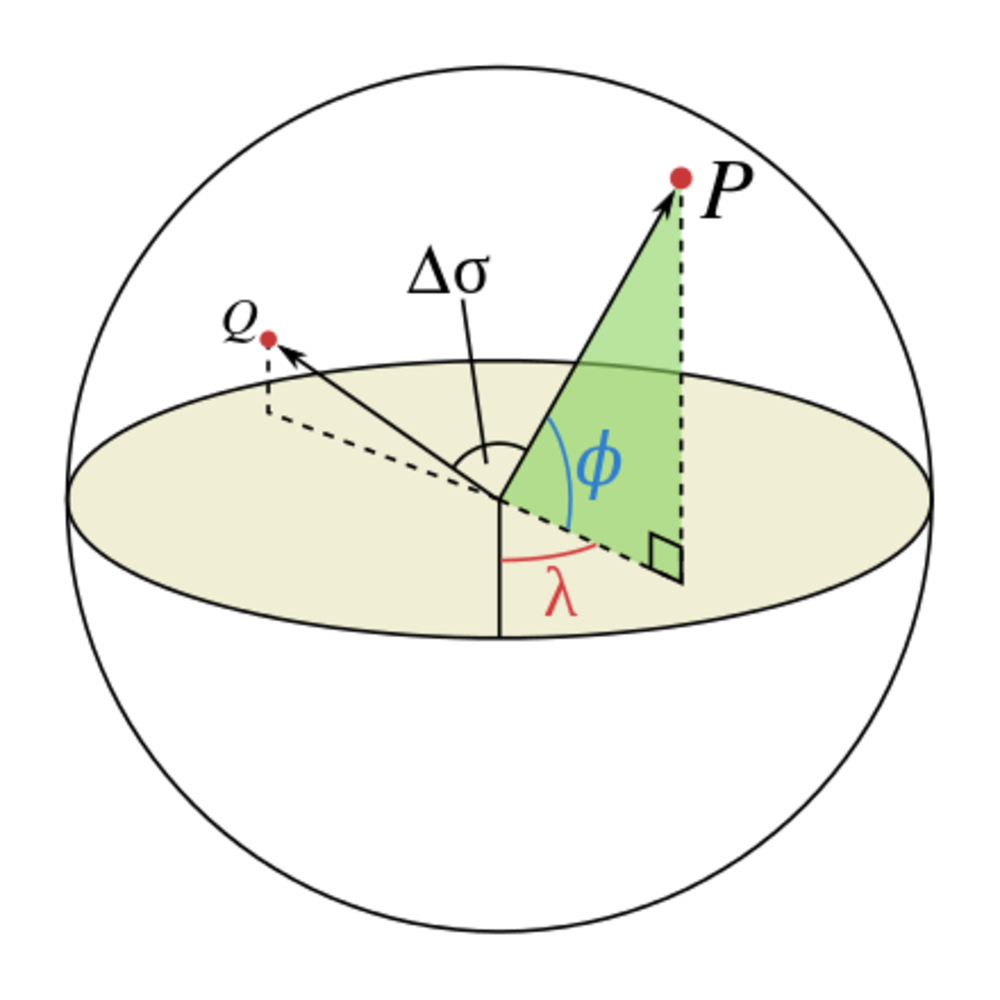
二点両方とも緯度経度の角度で位置を与えられるものとして、 \(\phi_1,\phi_2 \)は緯度、\(\lambda_1,\lambda_2\)は経度を表すものとする.

Great-Circular Distanceにおける弧度\(\theta\)(二点を通る断面で見たときのなす角度)の求め方は以下の式. $$\theta = arccos(sin\phi_1\cdot sin\phi_1+cos\phi_1\cdot cos\phi_1\cdot cos(\Delta \lambda ) )$$ この式と半径\(r\)から求める球面状の距離\(d\)は、 $$d = r\theta $$

Haversine Formulaは上記の式の精度を改善した以下のような式を提案した. $$\theta = 2arcsin\sqrt{sin^2 (\frac{\Delta \phi}{2})+cos\phi_1\cdot cos\phi_1\cdot sin^2 (\frac{\Delta \lambda}{2} )} $$ この式と半径\(r\)から求める球面状の距離\(d\)は、 $$d = r\theta $$

Vincentyはさらに以下のようなより正確な式を与えた. $$\theta = arctan (\frac{\sqrt{(cos\phi_2 \cdot sin(\Delta \lambda))^2 + (cos\phi_1\cdot sin\phi_2 - sin\phi_1 \cdot cos\phi_2 \cdot cos(\Delta \lambda )}} {sin\phi_1 \cdot sin\phi_2 + cos\phi_1 \cdot cos\phi_2 \cdot cos(\Delta \lambda )})$$

Vincenty法は、かなりの精度で回転楕円体としての地球上の二点間の距離を求めることができ、頻繁に使用される.