-
 @ThothChildren
@ThothChildren
- 2018.10.21
- PV 426
トポロジカルソート
ー 概要 ー
トポロジカルソートは、依存関係のある複数の要素を依存関係の順序を崩さずに並べるソート.プログラムに依存関係があるときや仕事の順序の決定などにトポロジカルソートは用いられる.
この章を学ぶ前に必要な知識
条件
- 依存関係のある複数要素
- 依存関係をたどると一周する"閉路"が存在しないこと
効果
- 依存関係を守った順序で並べられる
- コンパイラのコンパイル順番や依存関係のある仕事をこなす順番を決められる
ポイント
- トポロジカルソートの解は複数ある
- 依存関係をグラフにしたときにハミルトニアン路があれあば解は一つ
- 手法によっては閉路があるかないかを判定可能
- 時間計算量はO(N+E) (Nはノード数, Eはエッジ数)
- 複数の解が幾らかをかぞえあげる方法は動的計画法によって実現する
解 説
トポロジカルソートは、依存関係のある複数の要素を依存関係の順序を崩さずに並べるソート.ノード数をNとしエッジ数をEとして、時間計算量はO(V+E)で完了する.
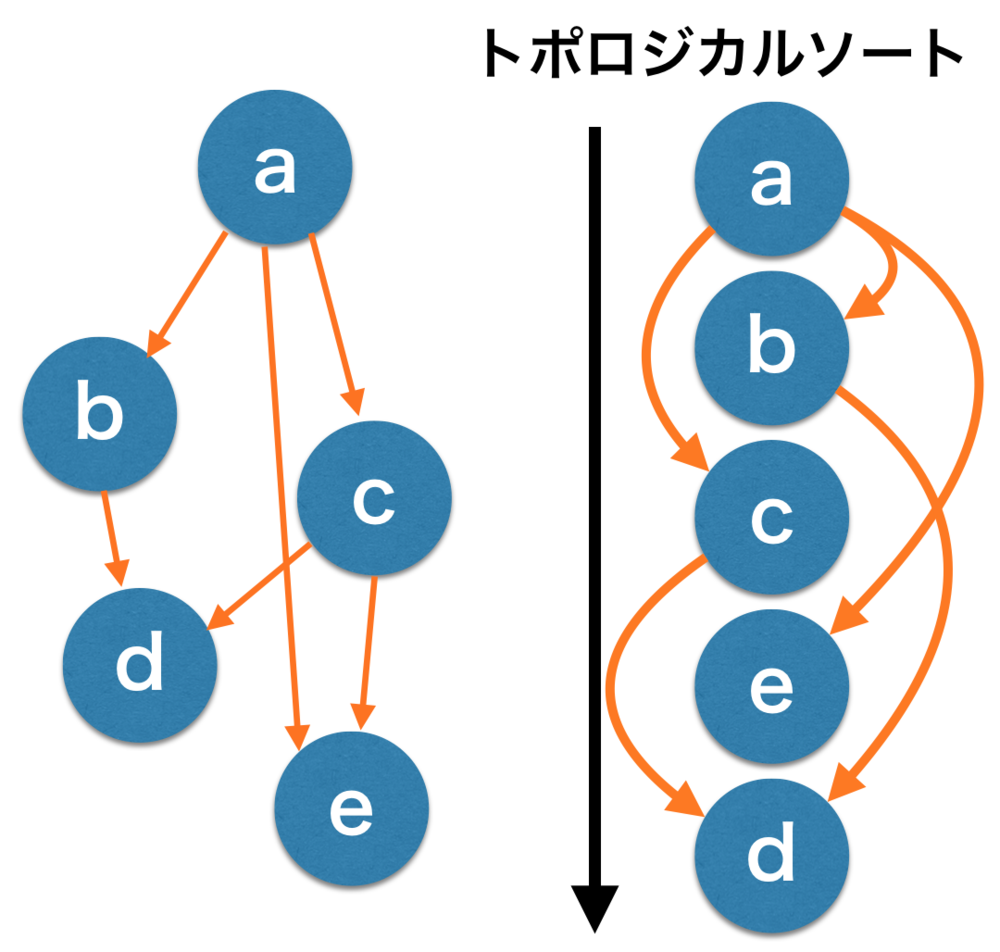
プログラムに依存関係があるときや仕事の順序の決定などにトポロジカルソートは用いられる. | トポロジカルソートとは |
 | トポロジカルソート概念図 |
1.トポロジカルソートのアルゴリズム | |
トポロジカルソートのアルゴリズムについて解説します.
この問題は解決する方法は主に二つあります(片方はベースが探索です).どちらも線形時間の処理すなわちO(V+E)の時間計算量になります.
・Kahnの方法(トポロジカルソート)
解がなければ循環がある.特定のノードの依存先を求めにくい
・Tarjanの方法(深さ優先探索)
こちらは循環があるかは別に確認が必要.特定のノードの依存先を求めやすい | トポロジカルソートのアルゴリズム |
1.1.Kahnの方法(トポロジカルソート) | |
Kahnの方法はいたってシンプルな方法です.
誰にも依存されていないノードはどんどん追加していいので、そのノードから追加します.
すると、新しく誰にも依存されていないノードが出てくるので、先ほど追加したノードの後ろに追加していきます.
あらかじめ用意する
・誰にも依存されいてないノードリスト
それでは、以下に流れを説明します. | Kahnの方法について |
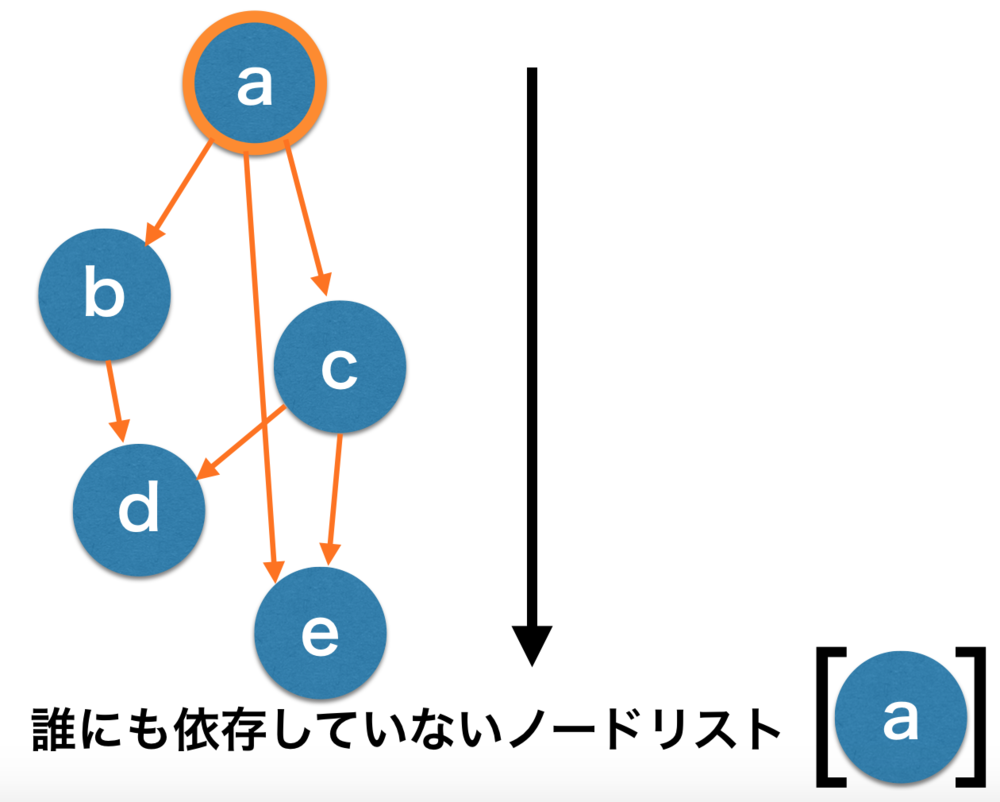 | まず初めの状態です.
誰にも依存していないノードはAだけです. |
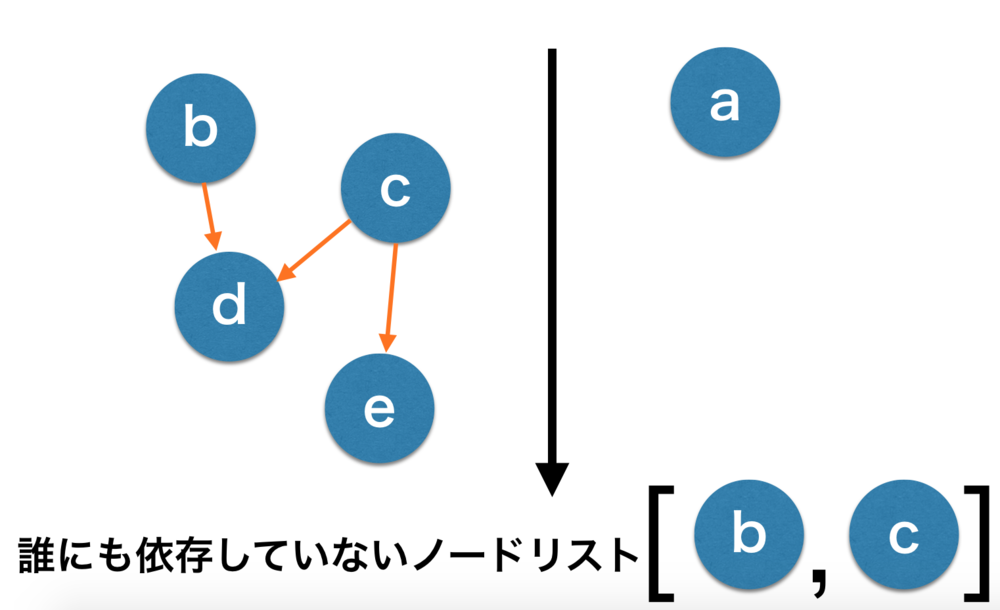 | aをソートの列の先頭に移動させて、
グラフからaとそこから伸びていたエッジを消します.
また、次に誰にも依存していないノードリストを作り直します. |
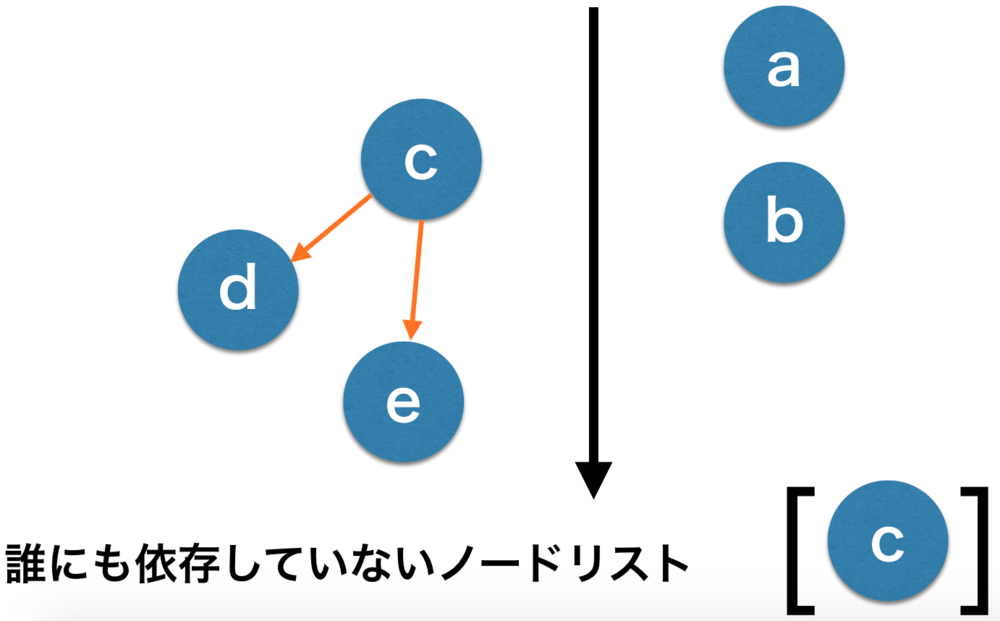 | 次はbをリストに追加しました.
ここでは、cでもbでもどちらでも構いません.
たまたまbを選択しました. |
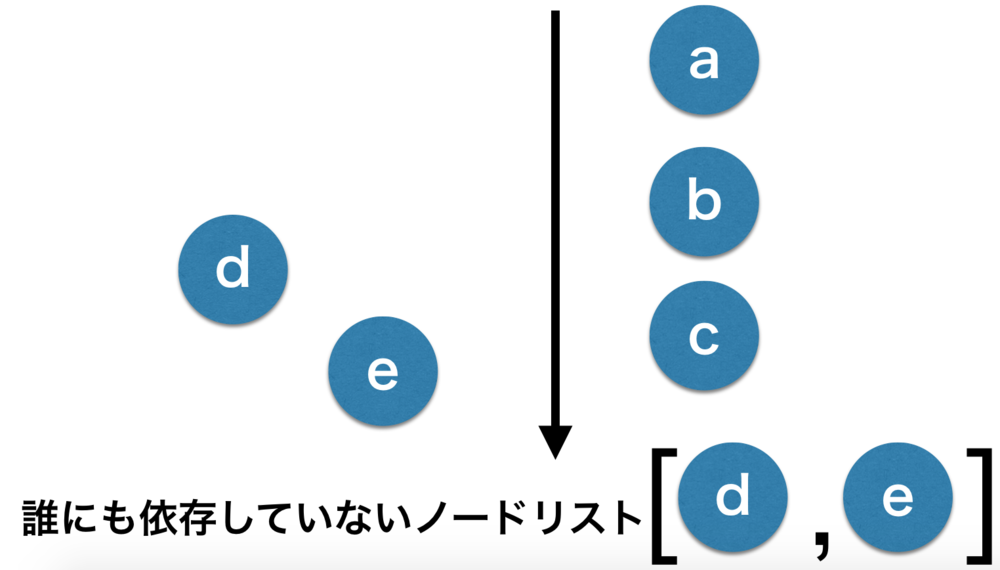 | 次にCを加えます.
するとノードリストが更新されます.
最後のd,eだけです. |
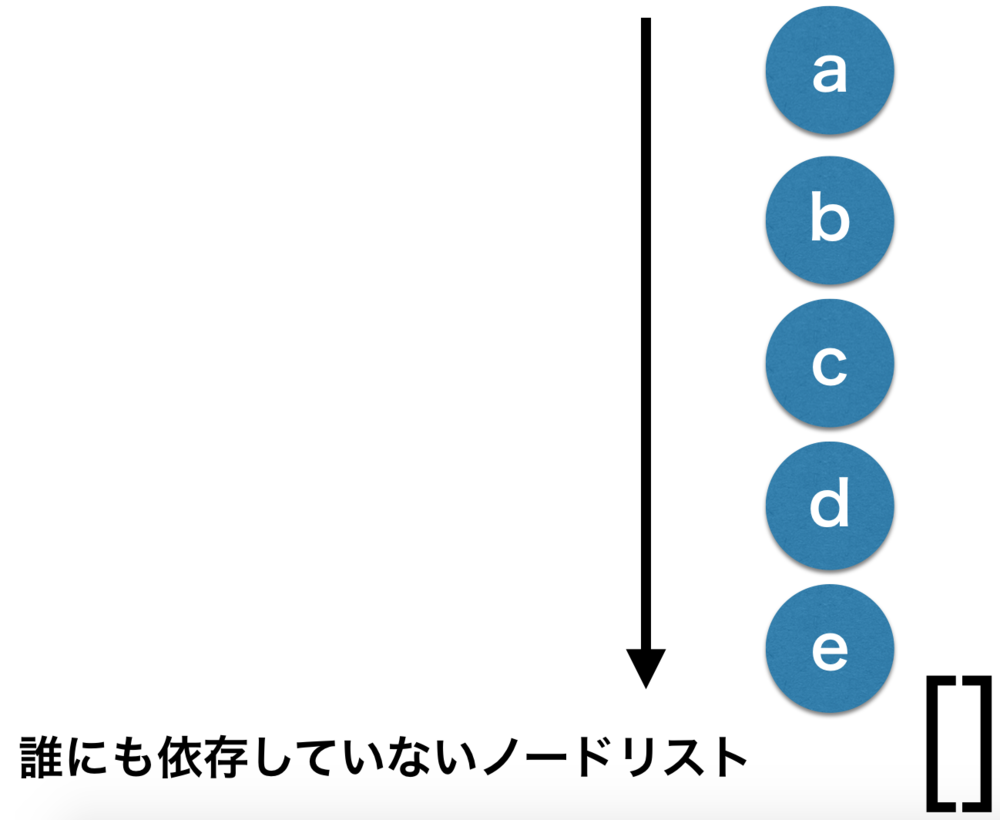 | これで終了です. |
1.2.Tarjanの方法 | |
Tarjanの方法は、深さ優先探索です.
グラフの上から深さ順に沿って、深く潜った帰り際に見つけたノードを登録していくことになります.必ずノードを追加していくときは、リストの先頭に加えます.
リストへの登録するときにはそのノードに依存している全てのノードは登録されていることになります.(深さ優先探索の性質) | Tarjanの方法 |
深さ優先探索に関してわからない場合は、リンクを確認ください. | 深さ優先探索 |
2.トポロジカルソートそのほか | |
解が複数あることに関しては先に述べた通りです.さきのkahnのソートの説明でもb,cやd,eはどちらを先に加えても構いませんでした.
複数解があるかどうか
解が複数あるかどうかはひとつ知る方法として、グラフの中にハミルトニアン路が含まれているかどうかがあります.もし含まれているなら1つしか解はありません.ないなら解は二つ以上あります.
全ての解を列挙したい
トポロジカルソートの列挙(トポロジカルソートの数え上げ)は、動的計画法(DP)を用いて行うことができます.
| トポロジカルソートの解について |
トポロジカルソートの数え上げについてはリンク先の参照ください. | 外部リンク トポロジカルソートの数え上げ |
トポロジカルソートを用いることでDAG(有効非循環グラフ)の最短経路をO(V+E)のオーダで求めることができます. | トポロジカルソートの応用例 |
この章を学んで新たに学べる
Comments
Reasons
知識: 深さ優先探索
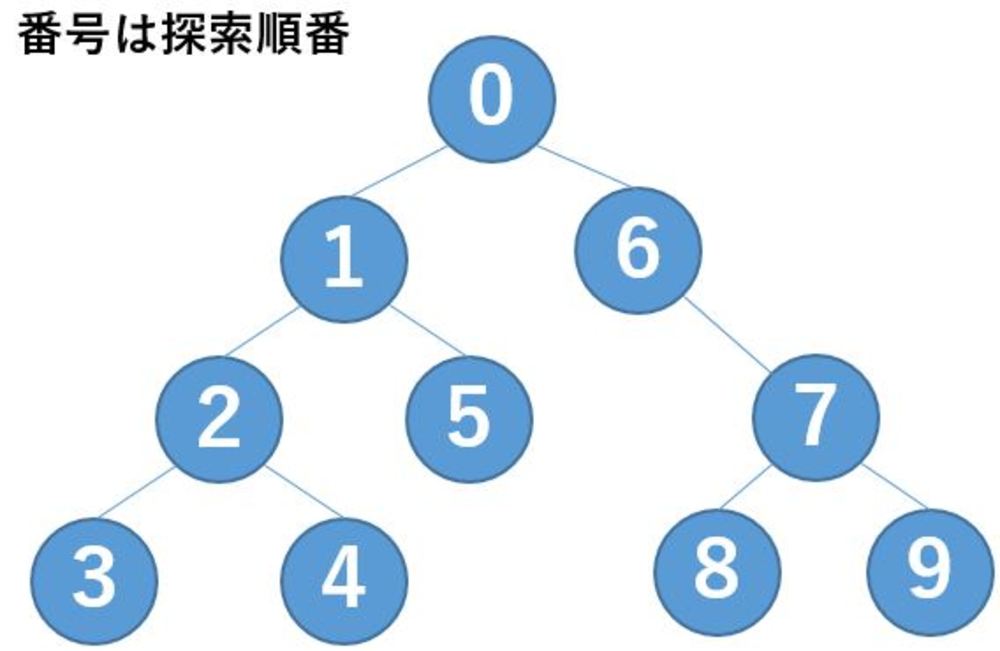
深さ優先探索はグラフデータの中でスタートのデータからとりあえずグラフの分岐がなくなるまで探索し、なくなったら少し戻って次の候補を探していく探索.データが深いところにありうる場合には幅優先探索でなくこちらを使用します.際限なく深くなりそうなときは最大深さを決めて途中で打ち切る場合もあります.通常幅優先探索より空間計算量ははるかに小さくなる.


