-
 @ThothChildren
@ThothChildren
- 2018.10.21
- PV 1515
Lucas Kanade法
ー 概要 ー
Lucas Kanade法は、金田らによって提案されたオプティカルフローの実現手段として代表的な手法の一つ.
この章を学ぶ前に必要な知識
条件
- 複数枚の入力画像
- 微小な時間に微小な移動しかないことが前提
効果
- 画像間のオプティカルフローを効率よく求めることができる
ポイント
- 大きな移動にも対応できるように画像サイズをピラミッド常に変化させて探索
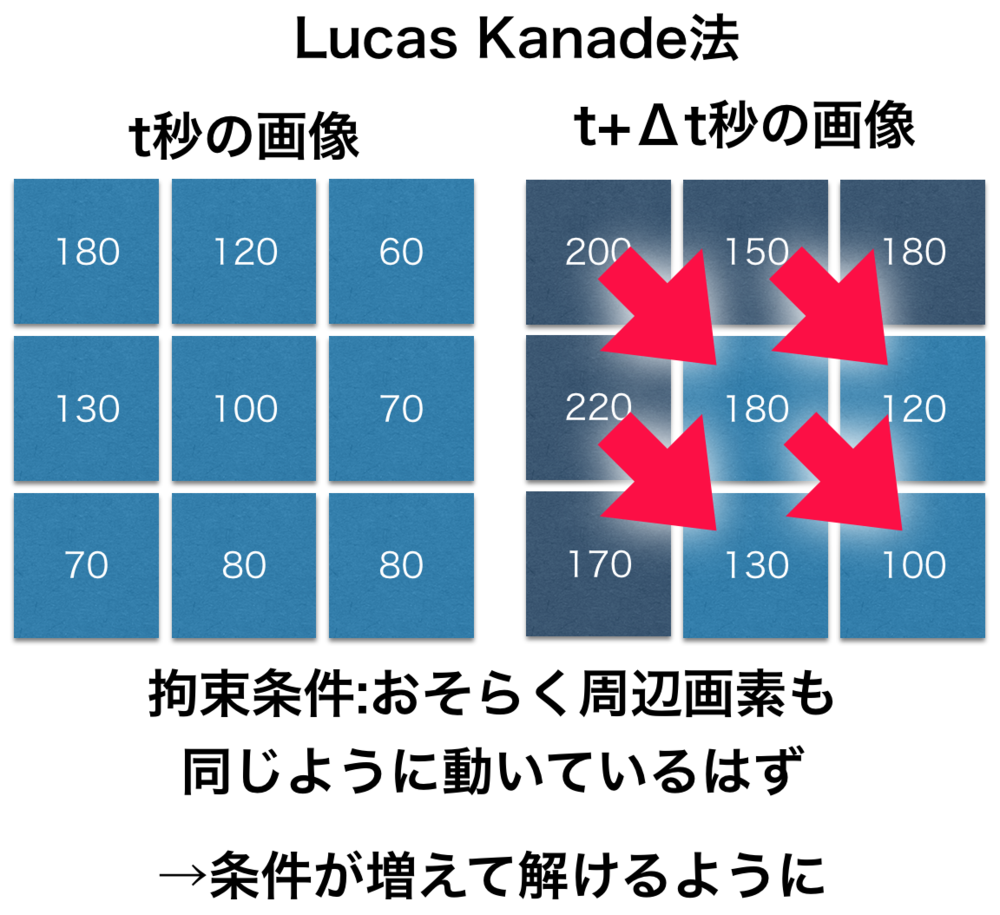
- 周辺の画素も同様の動きをするという拘束条件で式を追加し、解を求めた
解 説
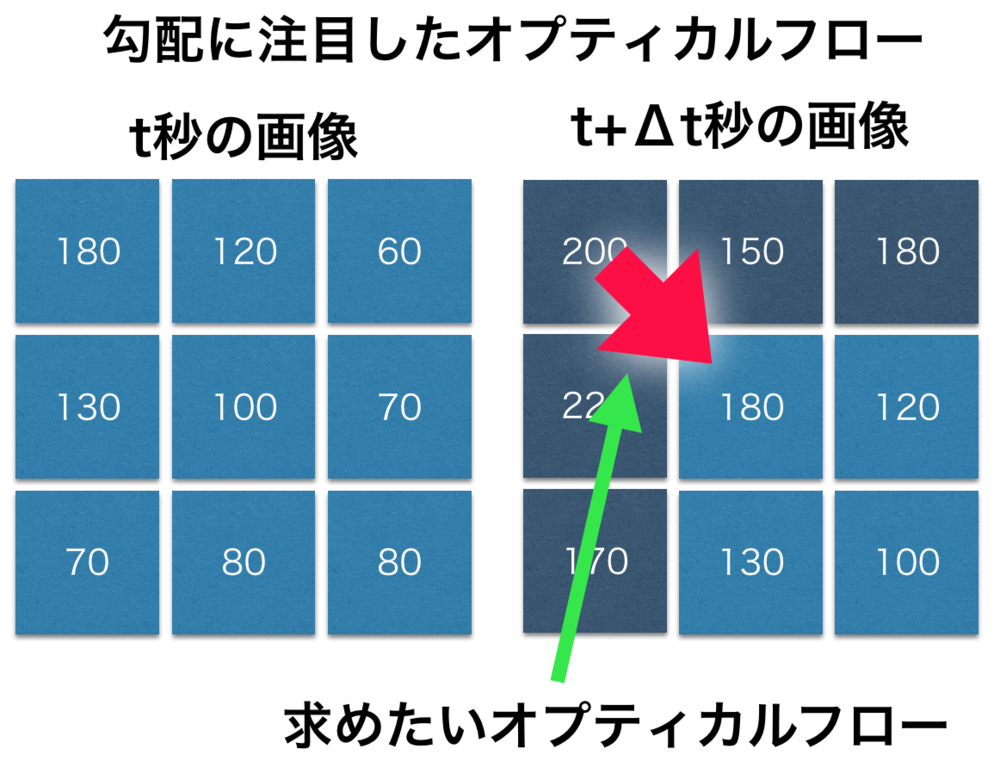
先に右の「勾配に注目したオプティカルフロー」を理解した上でこちらを読んでください.続きになっています. | 勾配に注目したオプティカルフロー |
Lucas Kanade法は、金田らによって提案されたオプティカルフローの実現手段として代表的な手法の一つ.勾配に注目した手法で、画像中を全探索して求める方法より計算量を抑えて求めることができる.
勾配に注目したオプティカルフローでは、不定な数が2つあり、式が1つしかなかったため、他に拘束条件とそれによって記述できる式が必要だった.
Lucas Kanade法では、
「周辺の画素も同じような動きをする」という拘束条件を導入することで解決. | Lucas Kanade法について |
$$0 = I_x \frac{\Delta x}{ \Delta t}+ I_y \frac{\Delta y}{ \Delta t} + I_t$$
\(I_x, I_y, I_t\)は注目画素のx偏微分、y偏微分、t偏微分です.
この\(\frac{\Delta x}{ \Delta t},\frac{\Delta y}{ \Delta t}\)が求めたいオプティカルフローでした.
この式は一つの画素に注目した式でしたが、
これを周辺の画素でも\(\frac{\Delta x}{ \Delta t},\frac{\Delta y}{ \Delta t}\)を共通なものとして複数の式にします.煩わしいので、\(\frac{\Delta x}{ \Delta t},\frac{\Delta y}{ \Delta t}\)を\(u,v\)と置き換えてまた注目している画素を\(p,q\)として式を書けば,以下のような連立方程式です.画素とその周辺8個に注目したものとします.
$$
\begin{eqnarray}
\left\{
\begin{array}{l}
0 = I_x(p,q) u+ I_y(p,q) v+ I_t(p,q) \\
0 = I_x(p+1,q) u+ I_y(p+1,q) v+ I_t(p+1,q) \\
0 = I_x(p-1,q) u+ I_y(p-1,q) v+ I_t(p-1,q) \\
0 = I_x(p,q+1) u+ I_y(p,q+1) v+ I_t(p,q+1) \\
0 = I_x(p+1,q+1) u+ I_y(p+1,q+1) v+ I_t(p+1,q+1) \\
0 = I_x(p-1,q+1) u+ I_y(p-1,q+1) v+ I_t(p-1,q+1) \\
0 = I_x(p,q-1) u+ I_y(p,q-1) v+ I_t(p,q-1) \\
0 = I_x(p+1,q-1) u+ I_y(p+1,q-1) v+ I_t(p+1,q-1) \\
0 = I_x(p-1,q-1) u+ I_y(p-1,q-1) v+ I_t(p-1,q-1)
\end{array}
\right.
\end{eqnarray}
$$
とんでもない式になりましたが、これを行列の形に直せば
$$
\begin{eqnarray}
\left(
\begin{array}{rrr}
I_x(p,q ) & I_y(p,q) \\
I_x(p+1,q ) & I_y(p+1,q) \\
\vdots \\
I_x(p-1,q-1 ) & I_y(p-1,q-1) \\
\end{array}
\right)
\left(
\begin{array}{rrr}
u \\
v
\end{array}
\right)
=
-
\left(
\begin{array}{}
I_t(p,q) \\
I_t(p+1,q) \\
\vdots \\
I_t(p-1,q-1)
\end{array}
\right)
\end{eqnarray}
$$
ちょっと騒々しいので文字で置き換えて
$$
\begin{eqnarray}
A\left(
\begin{array}{rrr}
u \\
v
\end{array}
\right)
=- b
\end{eqnarray}
$$
この方程式をとけば良いわけです.
2個しか不明な変数ないのに、さっきまで足りなかった式が一気に9個に増えても意味ないのではと思われるかもしれませんが、
現実問題全てを綺麗に満たせる\(u,v\)はありません.それは今まで様々な無理やりな仮定を置いていたため、微妙にそれぞれにもっとも適したu,vがずれるためです.
| Lucas Kanade法の詳細 |
さて、それではどのように上記式を求めるかと言えば,
もっともそれぞれの式の誤差を小さくする最小二乗法がもっとも一般的です.
そのときにどのような解が与えられるかは、すでにわかっており以下のような式が解であることがわかっています.
$$\begin{eqnarray}
\left(
\begin{array}{cccc}
u \\
v \end{array}
\right)
= -(A^TA)^{-1}A^Tb
\end{eqnarray}$$
これで特定の画素に注目したオプティカルフローが求まります. | Lucas Kanade法の詳細のラストパート |
詳細の説明は終わったので再度全体の流れを確認します.
1. まずオプティカルフローの求まりやすい特徴的な点を画像から見つける.
のっぺりている箇所や周りでも同じような画素が多いところは特徴点に不安定になるので選ぶべきではないためです.
2. 求めた特徴点に関して以下オプティカルフローを求める.
3. 前後の画像を用いて、注目している画素とその周りのIx,Iy,Itを求める.
4. それらから上記のu,vを求める最小二乗法を求める.その解がオプテキカルフローです.
これだけです. | Lucas Kanade法の全体の流れ |
 | Lucas Kanade法の概念の図解です. |
この章を学んで新たに学べる
Comments