Thue-Morse列

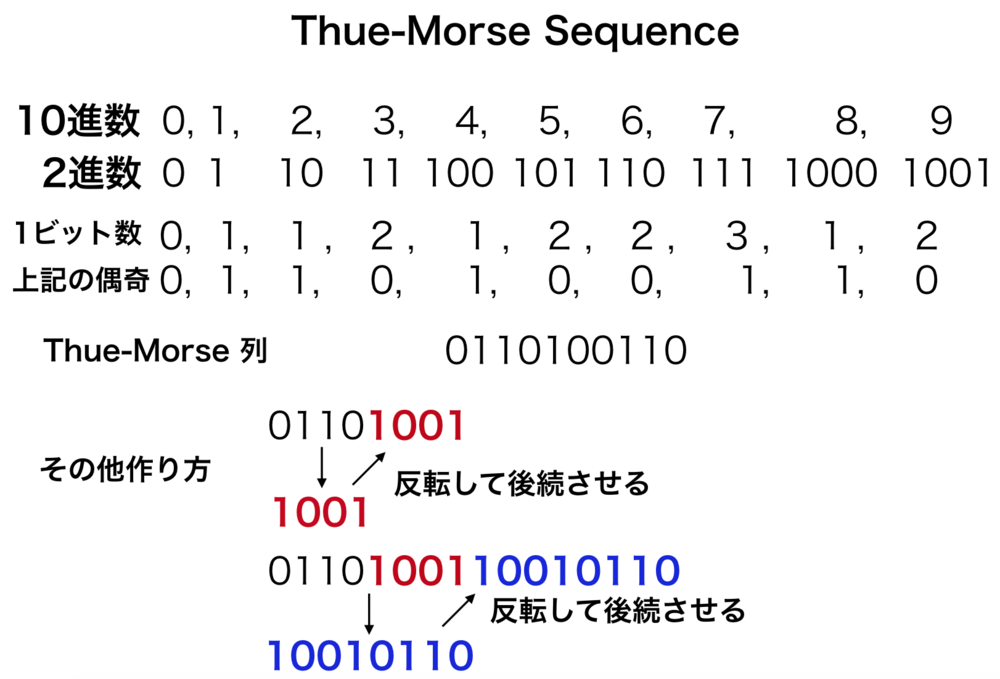
Thue-Morse列は、数を数え上げていくときにその数字を2進数で表記した時の1の偶奇を並べた列. すなわち、0,1,2,3...の数字を二進数表示にして、0, 1, 10, 11, ...その1の数が偶数個ある場合は0、奇数個ある場合は1とする. 特徴 ・列の中に現れるいかなる長さのパターンも3回以上連続しない.

Thue-Morse Sequenceの作り方は、先に述べた厳密な定義以外に、他二つの作り方がある. まず置換ベース. 文字列の置換を繰り返して作成 ・0を開始. ・0→01, 1→10に置換する. 上記ルールで行うと $$0\rightarrow01\rightarrow0110\rightarrow01101001\rightarrow0110100110010110$$

次はビット操作ベース ビット操作によって作成 ・\(T(n-1)\)があったら $$T(n) = T(n-1) NOT(T(n-1))$$ 自身をビット反転させたものを自身の後ろに繋げる. すなわち\(T(n-1) = 0110\)なら $$T(n) = 0110\ 1001$$ のようになる.

先手が有利になってしまう操作があり、それを交互に行うと最後まで先手が有利なことが多い. そこでどちらかが有利にならないようにThue-Morse Sequenceの順番にする方法などがあります(Fair Share Sequence).共有しているリソースなどがあるときなどにも先手必勝にならないようにすることができます.

他に参考になりそうなリンクを貼っておきます.