-
 @ThothChildren
@ThothChildren
- 2018.10.18
- PV 426
De Bruijn列
ー 概要 ー
De Bruijn列(ドゥブリュエイン列)はある文字または数字の集まりから指定長さの組み合わせを考える時に、それらの組み合わせを必ず一つ含む列."a,b"を使った3文字の列を考えると、"aaa","aab","aba","baa","bbb","bba","bab","abb"なので"aaababbbaa"がDe Bruijn列.

この章を学ぶ前に必要な知識
条件
- 文字または数字の組み合わせを決めておく("a,b,c"や"0,1")
- 何文字の組み合わせにするか決めておく("aaa"なら3,"010101"なら6)
効果
- Enter操作を含まない総当たり攻撃で効率よく試す列を得る
- 指定の文字と数字で指定の長さの全組み合わせを必ず一つを含む列を得る
- 通常の総当たり攻撃の1/n(組み合わせの長さ)の処理時間になる
- 回転角度を符号化する際にも使用できる
ポイント
- de Bruijn グラフ(ドゥブリュエイングラフ)を作成し、そのハミルトニアン路を求めるとDe Bruijn列(ドゥブリュエイン列)を得る
解 説
De Bruijn列(ドゥブリュエイン列)はある文字または数字の集まりから指定長さの組み合わせを考える時に、それらの組み合わせを必ず一つ含む列.
例
"a,b"を使った3文字の組み合わせを考えると、"aaa","aab","aba","baa","bbb","bba","bab","abb"なので
"aaababbbaa"がDe Bruijn列.
この中に確かに(aaa, aab, aba, bab, abb, bbb, bba, baa)の8通り全て一度だけ含まれている
| De Bruijn列(ドゥブリュエイン列)とは |
De Bruijn列の作り方は幾らかあるがここでは、
De Bruijnグラフを作成して、ハミルトニアン路を見つける方法を紹介.
アルゴリズム
ここではk文字("0","1"ならk=2)を使ってn文字("01011"ならn=5)の長さの組み合わせを作る場合を考える.
以下例は、2文字4文字の組み合わせを想定.下の図に対応.
1. まず(n-1)の組み合わせを列挙
000, 000, 001, 011, 111, 111, 110, 101, 011,110, 100, 001, 010, 101, 010, 100, 000.
2. これらをノードにしたDe bruijnグラフを作成.
3. このグラフを元に点を一度しか通らないハミルトニアン路を見つけ出す.
4. 見つけたハミルトニアン路に沿って文字列を集めると,
(000 → 000 → 001→ 011→ 111→ 111→ 110→ 101→ 011→
110→ 100→ 001→ 010→ 101→010→ 100→ 000)
5. 上記4.の数列の先頭の数字を集めていくとDe Bruijn列となる.
DeBruijn列 : 0000111101100101000
| De Bruijn列の作り方 |
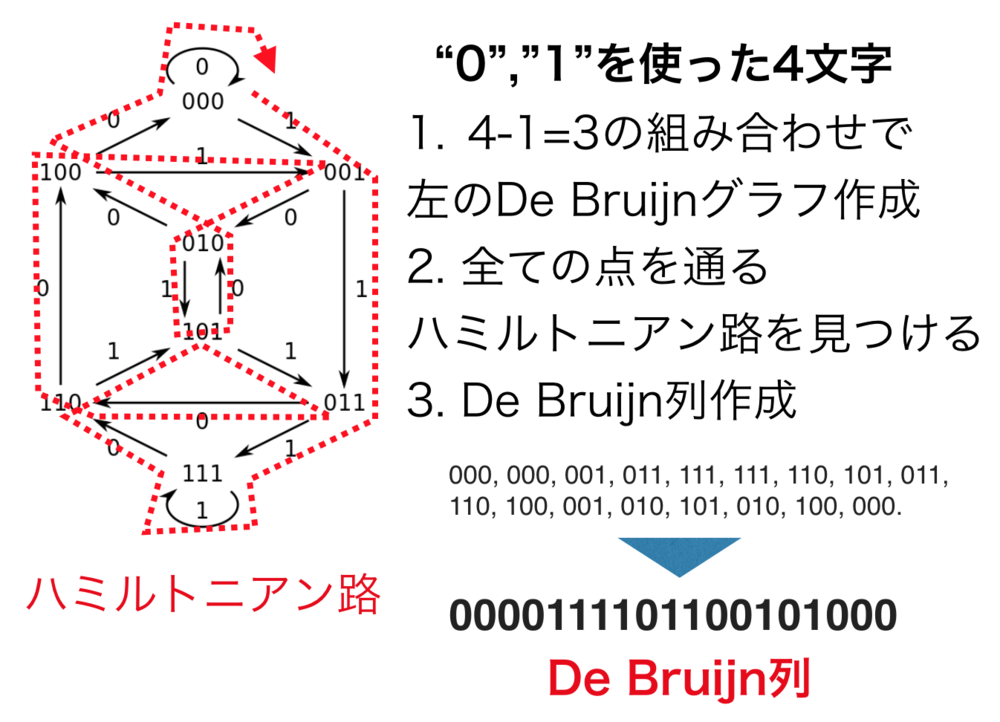 | アルゴの図解.
図はWikipediaより引用.
|
Brute Force(総当たり攻撃)にて
仮に一度決定するごとに入力のし直しがないのならば(入力した末尾の文字列で判定. Enterキーを押さないなら)、入力回数を減らし、総当たり攻撃の効率を高めることができる.
ほかには、「回転角度を示す符号」にするや「最上位の1が立っているビット」を見つける際などに役に立つ.
| De Bruijn列の使い時 |
この章を学んで新たに学べる
Comments


