-
 @ThothChildren
@ThothChildren
- 2018.10.15
- PV 596
Kittlerによる二値化フィルタ
ー 概要 ー
Kittlerによる二値化フィルタは、背景と前景に二つの異なる正規分布を仮定して平均的に誤り率を下げるように閾値を調整する二値化フィルタ.大津の方法では、片方の分布が偏っている場合は閾値が極端に寄ってしまっていたが、Kittlerの方法ならその問題が起こらない.
この章を学ぶ前に必要な知識
条件
- 入力画像はグレースケール画像
- 閾値の設定は不要
- 前景と背景が正規分布に従うと仮定できる
効果
- 出力画像は二値化画像
- 大津の方法より柔軟な閾値を選択できる
ポイント
- 閾値を引いた時にクラスの分類をなるべく間違わないような閾値を選択
解 説
Kittlerによる二値化フィルタは、背景と前景に二つの異なる正規分布を仮定して平均的に誤り率を下げるように閾値を調整する二値化フィルタ.人手であらかじめパラメータを決める必要はない.
Kittlerの方法
0. 任意の閾値を指定する.
1.「背景の正規分布」と「前景の正規分布」を求める.
閾値に従って、背景グループと前景グループのピクセルでまとめる.
各グループの値から、平均と分散と比率を求める.
2. 1.で求めた値から下記の評価値を計算する.\(T\)は閾値,\(w_1,w_2\)は比率,\(\sigma_1,\sigma_2\)は分散.
$$J(T) = w_1(T)log(\frac{\sigma_1(T)}{w_1(T)})+w_2(T)log(\frac{\sigma_2(T)}{w_2(T)})$$
3. 閾値を変えながら2の評価値が最小になる閾値を求める.
大津の方法では、片方の分布が偏っている場合は閾値が極端に寄ってしまっていたが、Kittlerの方法ならその問題が起こりにくい. | Kittlerによる二値化フィルタとは |
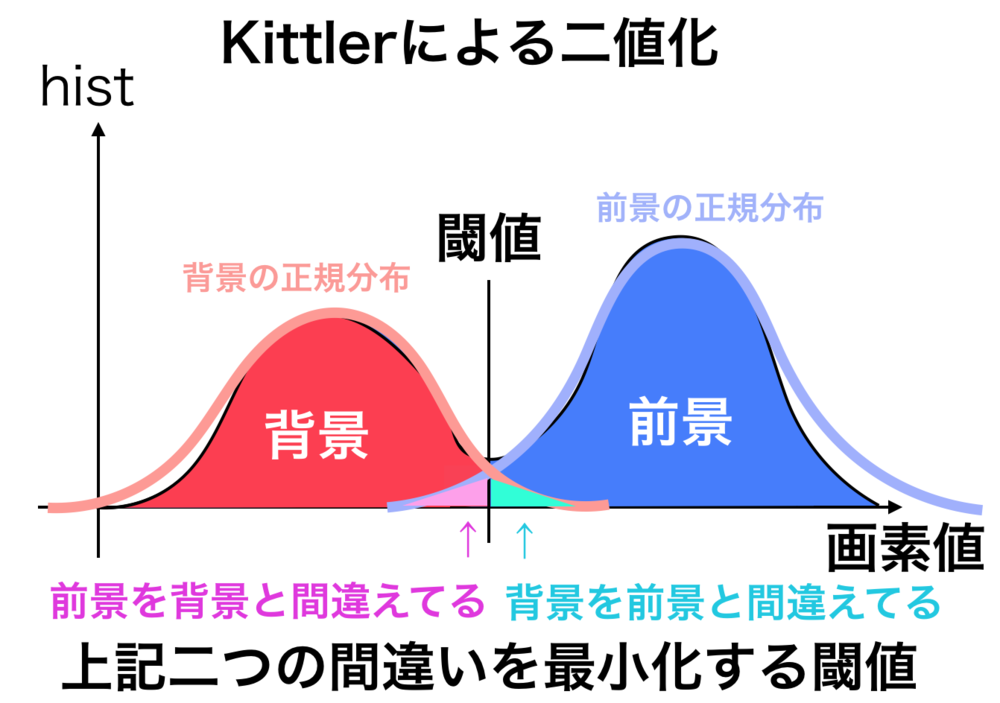
 | Kittlerによる二値化の図
二つの誤りの部分を最小にするような閾値を選択する必要がある.
|
この章を学んで新たに学べる
Comments


