RRT

RRT(Rapidly-exploring Random Tree)は高次元空間における探索を効率的に比較的高速的に行うことのできる探索手法. これを用いて自由度の高いロボットアームの軌道探索や経路探索などが行われることが多い. アルゴリズムがシンプルで実装も容易だが、パスを求めた場合などは最適な経路に修正する必要がある.最適なパスとは限らない. また、障害物などの判定も容易で、制限も入れやすいのも特徴.

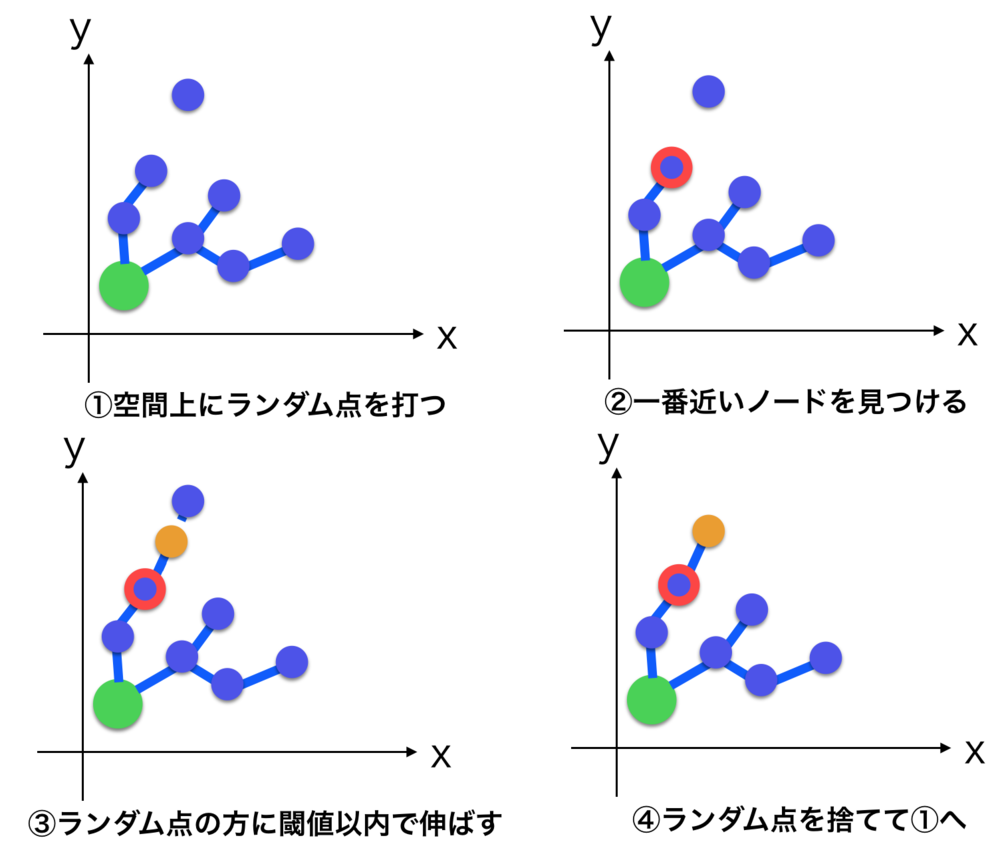
RRTのアルゴリズムは以下のようにシンプルになっている. 事前 q_init：初期位置 tree : 探索してノードを加えるツリー distance_max : ノードを加えるときの既存ノードからの最大距離. K : 探索するノードの数 アルゴリズム 1. 初期のノードを用意する. 2. 以下3.~6.をK回繰り返す. 3. ランダムq_randな点を空間からサンプリングする. 4. 3.で得たランダムな点q_randにもっとも近いノードq_nearをtreeから探す 5. q_nearからq_randに枝を最大distance_maxで伸ばし新しいノードq_newを作る. 6. q_newをtreeに加えて、q_randは捨てる.

RRTはランダムな点を打ち、もっとも近いノードから枝を伸ばすことで、 まだ未探索の領域を優先して探索するようになっている. これはボロノイ面積に比例して新しい点が作られるためである. また、スタートからゴールまでのパスの探索をするようなタスクにおいては、 ランダム点を取るときに一定の割合でゴールを点として選択することで、ゴールにバイアスをかけた探索を行うようにすることがある. また、狭いパスを通らなくてはならないような探索においては探索が難しくなる欠点もある.

ボロノイ図とは、空間をもっとも近い点で分割した図形のこと. 今回のRRTでは新しい点をもっとも近い点に割り当てることになるため、ボロノイ領域の面積が大きい点がRRTで新しい点を選ぶときに当然その領域が選ばれやすくなる.

実際にRRTを体験できるページへのリンクを貼っておきます. こちらでどのように障害物を配置してもランダムに枝を伸ばして、RRTがパスを見つけているのを見れるかと思います.