この章を学ぶ前に必要な知識
条件
- 二つの平面の法線ベクトル
効果
- 二つの平面間のなす角度が求まる
ポイント
- 平面のなす角度は二つの平面の法線ベクトルがなす角度に等しい
解 説
平面と平面が交わるときになす角度、交わる角度は簡単に求めることができます.
二つの平面が交わる角度はその法線ベクトルのなしている角度に等しいです.
法線ベクトルとは平面から垂直な方向を示しているベクトルです.これは平面の係数から求めることが可能です. | 平面と平面のなす角度 |
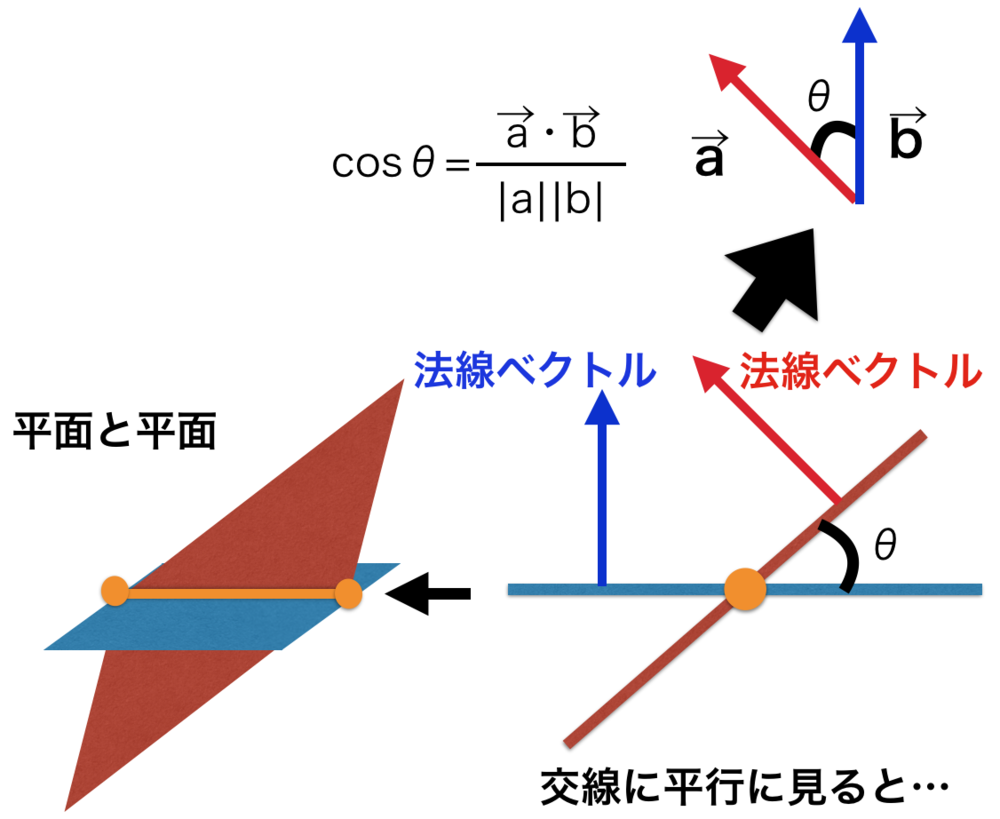
 | 平面と平面のなす角度のイメージ図 |
上記の図のように、平面と平面が交わっている交線と平行に見てみるとあたかも二つの直線が交わっているのと同じように見えます.
この二つのなしている角度を求めればよいことになります.
そのとき平面の二つの法線ベクトルのなしている角度が、二つの平面のなしている角度になることが簡単にわかります.
そうなると法線ベクトルのなしている角度を求めることになりますが、
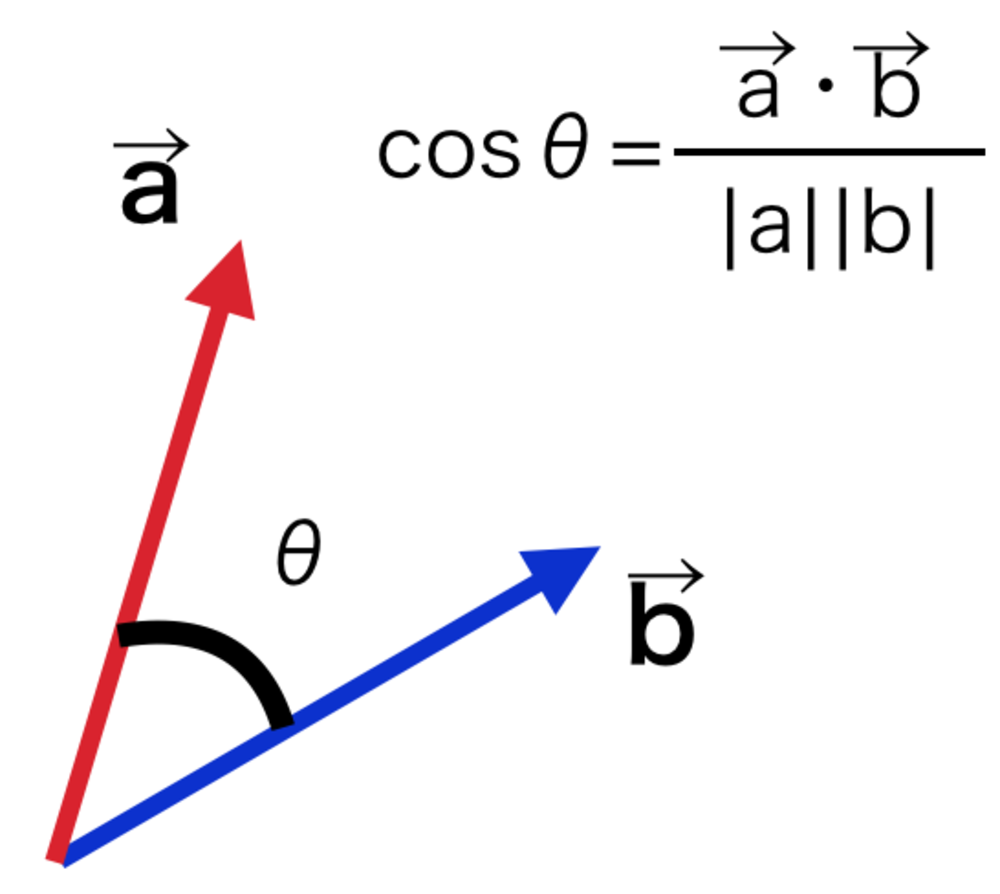
これはリンクにあるように、ベクトルの内積から求めることができます. | ベクトルのなす角度 |
1.例題 | |
それでは二つの平面のなしている角度を求める例を見てみましょう.
$$1 = x - y + z$$
$$5 = 2x + y + 3z$$
の二つの平面があるとします.
この時法線ベクトルはそれぞれの係数から、
$$(1, -1, 1), (2, 1, 3)$$
とわかります.
この法線ベクトルの内積から\(\theta\)を求めれば、平面のなす角度です.
$$cos \theta = \frac{\vec{a}\cdot \vec{b}}{|\vec{a}||\vec{b}|} = \frac{1\cdot2 +(-1)\cdot1+1\cdot3}{\sqrt{1^2+(-1)^2+1^2}\sqrt{2^2+1^2+3^2}} = \frac{4}{\sqrt{42} }$$
あとは\(cos\theta = \frac{4}{\sqrt{42}}\)は\(\theta\)がいくらか求めればなしている角度が求まります. | 二つの平面のなしている角度を求めてみる. |
この章を学んで新たに学べる
Comments
 @ThothChildren
@ThothChildren