-
 @ThothChildren
@ThothChildren
- 2018.9.10
- PV 580
リヤプノフの安定性
ー 概要 ー
リヤプノフの安定性に関してまとめているページです.主な用語としては、安定、漸近安定、一様安定、大域的漸近安定と呼ぶ状態がある.安定性は複数の定義のされ方があるため、「リアプノフの意味で安定」と明示的に呼ぶことがある.
この章を学ぶ前に必要な知識
条件
- システムが特定の方程式f(t,x)で記述できる
- いかなる時間でも(任意のt)でf(t,x)=0となるxを平衡点
- 図のδの大きさの円は点の初期位置が含まれる場所
- 図の黒点は、方程式に従い時間とともに移動している点
効果
- 任意の時間でεに点が収まるための初期位置δが存在:安定
- 上記の安定のときにδが初期の時間に関係ない:一様安定
- 上記の安定のときに無限時間が経つと点が平衡点に収束:漸近安定
- 上記の漸近安定と異なり、任意の初期位置から初めても平衡点に収束する:大域的漸近安定
ポイント
- 平衡点から少し離れているときに点がどのように動くかを見極める
解 説
リヤプノフの安定性に関してまとめています.
主な用語としては、
・平衡点
・安定
・漸近安定
・一様安定
・大域的漸近安定
と呼ぶ状態があります.
安定性は複数の定義のされ方があるため、「リアプノフの意味で安定」と明示的に呼ぶことがあります. | リヤプノフの安定性について |
あるシステムが
$$f(t,x)$$
と書くことができるとします.
この時に、任意の時間で
$$f(t, x_e) = 0$$
を満たす\(x_e\)を平衡点と呼びます.少なくとも平衡点ではバランスがとれることが保証されるが、システムによってはほんの少しずれるともう平衡点に戻らないものや平衡点からずれても再度平衡点に戻るようなものもあり、システムの特性に依ります.
ある時間\(t_0\)からある点\(x_0\)から始めた時に、その\(x\)にある点は方程式に従って、少しずつ遷移していきます.その移動が時間が経つにつれて(無限時間たったとして)どのようになって動いていくか(軌跡を描くか)を考察します. | リヤプノフの安定性の前提 |
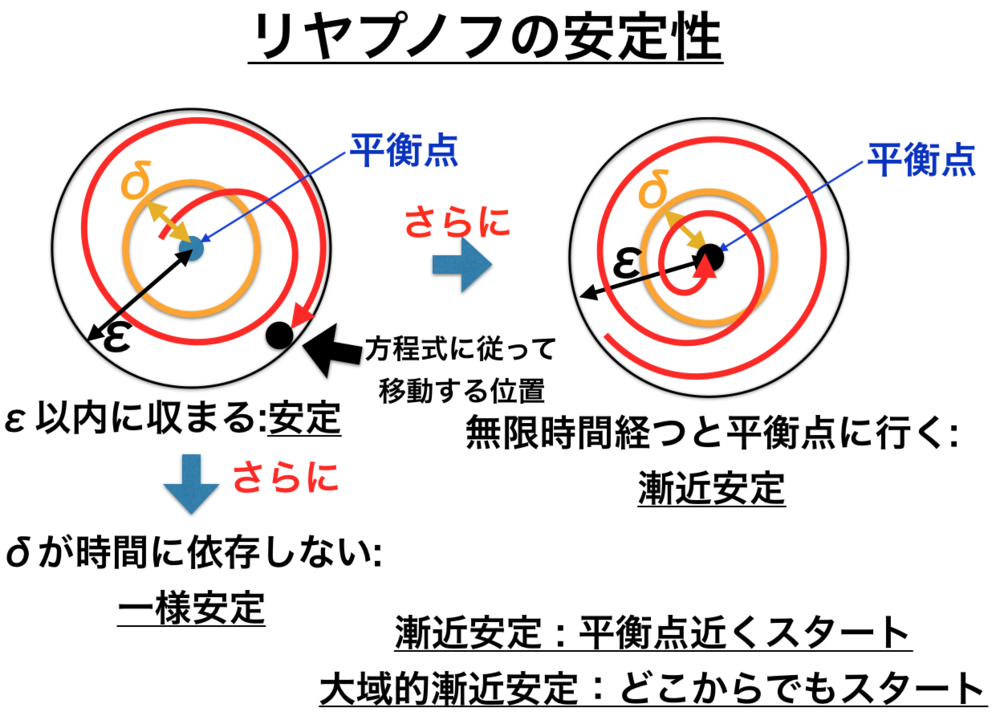
 | リヤプノフの安定性に関してまとめた図
黒い点が移動した跡が赤い軌跡として表示されている.
"安定"というのがベース.
δが時間依存しないと一様安定
平衡点の近くから始めて無限時間経って平衡点に収束するなら漸近安定
任意の場所から始めて無限時間経って平衡点に収束するなら大域的漸近安定
|
上記に書いてある通りですが、今一度記しておきます.
安定
任意の開始時刻\(t_0\)から\(x(t_0)\)がある\(\delta\)に含まれている時に任意の時間\(t\)においても\(x(t)<\epsilon\)となるような\(\delta(\epsilon,t)\)が存在する.
(εを決めたら、それに収まるように\(t_0\)に始まる領域δがいつでもあるよということ)
一様安定
上記の安定を守りつつ、\(\delta(\epsilon )\)で\(\delta\)を決められる.開始時間は関係ないときにこれを一様安定という.
漸近安定
上記の安定を守りつつ、十分平衡点に近いところから\(x_0\)を始めたとして、\(t\rightarrow \infty \)のときに、\(x(t)\rightarrow x_e\)(平衡点)となるとき、これを漸近安定と呼ぶ.つまり時間が経ったら平衡点に収束するということ.お盆に入れたボールがいずれ盆の底に向かう状態.
大域的漸近安定
漸近安定では平衡点の近いところという条件があったが、そうではなくいかなる場所から始めても平衡点に収束するとき、これを大域的漸近安定と呼ぶ.これはすなわちこのような平衡点が1点しかないことを示してもいる.
| リヤプノフの安定性のまとめ |
この章を学んで新たに学べる
Comments


