-
 @ThothChildren
@ThothChildren
- 2018.9.8
- PV 246
垂れた紐をモデル化した曲線が欲しい
ー 概要 ー
両端を持った時に垂れた紐をモデル化した曲線についてまとめたページです.垂れている紐の任意の位置での力学的な釣り合いの式から垂れている紐をモデル化することができ、一般的にカテナリー曲線(懸垂線、懸垂曲線)と言います.
この章を学ぶ前に必要な知識
条件
- 対称的に紐の両端を持っている
- 紐の線密度は場所によらず一定
- 紐がのびることはない
効果
- 垂れた紐をモデル化した曲線はカテナリー曲線(懸垂曲線、懸垂線)
- 曲線はcoshで表される
ポイント
- 懸垂線は原点付近は放物線で近似可能
- 懸垂線の方程式は力学的な釣り合いの式から導出可能
解 説
両端を持った時に垂れた紐をモデル化した曲線は一般的にカテナリー曲線(懸垂線、懸垂曲線)と言います.
垂れている紐の任意の位置での力学的な釣り合いの式から垂れている紐をモデル化することができます.
この曲線は、条件が以下のときに成立します.
・紐がどの点でも線密度が均一
・紐が伸び縮みしない
・紐の両端を同じ高さで対称的に持っている
| 垂れた紐をモデル化した曲線が欲しい |
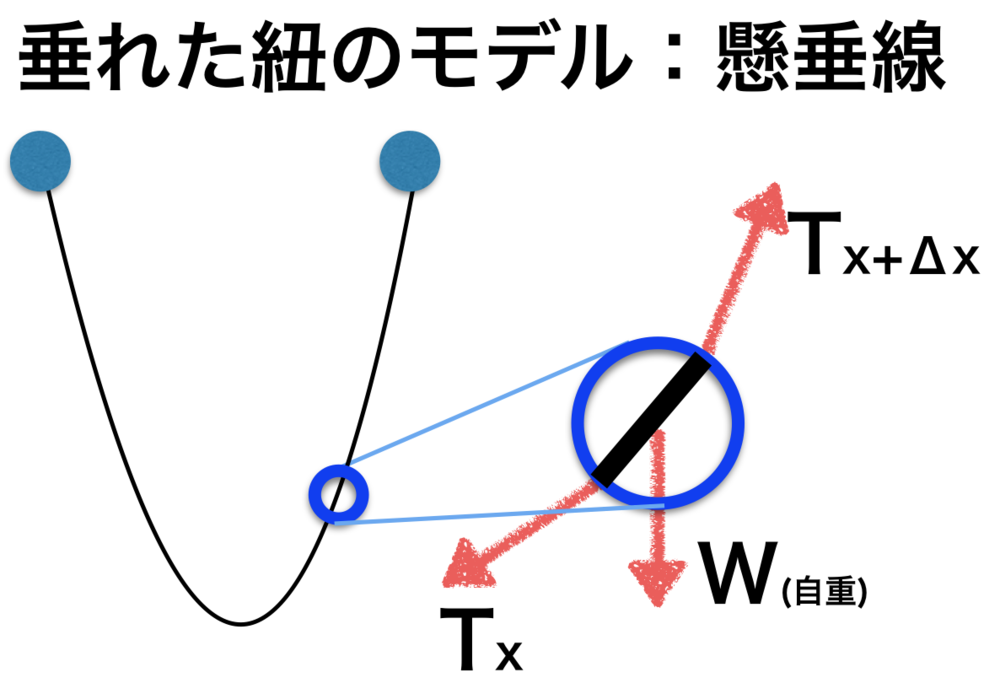
 | 垂れた紐のモデルの様子です.
図の右側のように、微小区間について力学の等式が成立することを
仮定することで曲線を求めることができます.
実際に導出しているサイトは多いので、ここでは簡単に曲線について触れるのみにします. |
垂れた紐のモデルは懸垂線で記述できることはすでに述べました.
実際の数式は以下のように記述できます.
$$y = a\cosh(x)=a\frac{e^{-x/a}+e^{x/a}}{2}$$
式から明らかに対称的になっています.明らかに以下が成り立ちます.
$$y = a\cosh(x)= a\cosh(-x)$$ | カテナリー曲線の形 |
原点周りでのカテナリー曲線の特徴について述べておきます.
先の方程式で記述される時\((x,y) = (0,a)\)が最も低い点、最下点の座標になります.
原点付近で\(e^{x},e^{-x}\)がマクローリン展開で\(1+x+\frac{x^2}{2!}+\dots\)で近似できるので、これらを上記の式に代入すると
原点の付近では、以下のような放物線に近似することができます.
$$y = a\cosh(x) = a + \frac{x^2}{2a}$$
原点では張力が真横を向くのも特徴の一つです. | 原点周りでのカテナリー曲線の特徴 |
この章を学んで新たに学べる
Comments


