ホップフィールドネットワーク

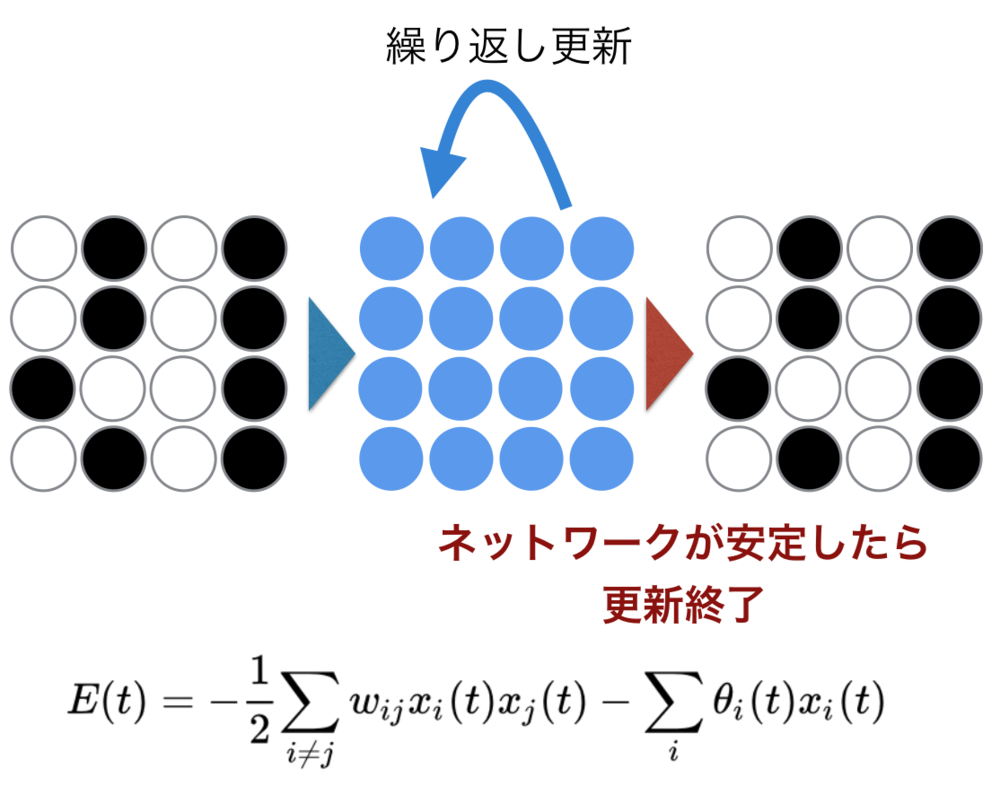
ホップフィールドネットワークとは、データを学習、想起させることのできるニューラルネットワーク.連想記憶のモデル. ネットワークの概要 ホップフィールドネットワークの学習と想起(繰り返し更新)の段階がある. ホップフィールドでは各ニューロンが全ニューロン間で相互に繋がっていてその重みを学習する.

学習の方法は幾らかある.学習は、少なくとも、局所的な学習ができ、また逐次的な学習ができればよい.逐次的というのは常に以前の学習データも含めて学習を行えること. ここでは有名な「ヘブ則による更新」を紹介する. n個のデータを含むデータ群xがあるときに二つのニューロンi番目とj番目の重み\(w_{ij} \)を学習するときは以下のようにして重みを計算する. $$w_{ij} = \frac{1}{n}\sum_{\mu =1}^n x_{\mu}^i x_{\mu}^j $$ 重みの学習は以上で終わりである.\(\mu\)番目のiとjを掛け合わせてそれをデータに渡って足し平均を取るだけである. 新しくデータを加えるときは、\(w_{ij}\)を\(n\)倍して\(x_{new}\)のijを足し合わせて\(n+1\)で割ればよいので、逐次的な学習ができることは明らか.

ホップフィールドネットワークにおける想起では、入力データをネットワークに入力したら更新を繰り返しネットワークの状態が変化しなくなった時点で出力を得ます. 更新のときにはエネルギー関数を最小化するように更新が行われていきますが、このエネルギーの更新は常に単調減少することが保障されているため、必ず終了します. しかし、エネルギーが大域極小値になるとは限らない エネルギー関数: \(s_n\)はn番目のニューロン $$E=-\frac{1}{2}\sum_{i\neq j}w_{ij}s_is_j + \sum_i \theta_i s_i $$

更新に際しては以下のようにして行っていく. 更新の方法には大きく ・非同期型 : ランダムまたは予め決められた順にニューロンを一つ選び更新. ・同期型 : すべてのニューロンを一斉に更新. がある i番めのニューロンの更新では以下のルールに則る. $$\begin{eqnarray} s_i = \begin{cases} 1 & ( if \sum_j w_{ij}s_i \geqq \theta_i ) \\ -1 & ( otherwise ) \end{cases} \end{eqnarray} $$ 上記を繰り返し行い、ネットワークの更新が行われなくなったら想起を終了. 各\(s_i\)の値を出力とする.